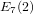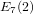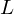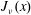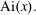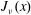Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Contents
The maximal subgroups of
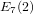 $E_{7}(2)$
$E_{7}(2)$
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 323-371
-
- Article
-
- You have access
- Export citation
A database of genus-2 curves over the rational numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation
Examples of linear multi-box splines
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2012, pp. 444-462
-
- Article
-
- You have access
- Export citation
The Minimal Degrees of Faithful Representations of the Sporadic Simple Groups and their Covering Groups
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 122-144
-
- Article
-
- You have access
- Export citation
Conjugacy Class Representatives in Fischer's Baby Monster
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 175-180
-
- Article
-
- You have access
- Export citation
The character table of a group of shape (2×2.G):2
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2010, pp. 82-89
-
- Article
-
- You have access
- Export citation
Identifying supersingular elliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2012, pp. 317-325
-
- Article
-
- You have access
- Export citation
Class numbers of real cyclotomic fields of composite conductor
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 404-417
-
- Article
-
- You have access
- Export citation
Approximations for the Bessel and Airy functions with an explicit error term
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 209-225
-
- Article
-
- You have access
- Export citation
Spider Diagrams
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 145-194
-
- Article
-
- You have access
- Export citation