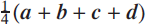 $${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
give the centre of mass of a quadrilateral?
$${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
give the centre of mass of a quadrilateral?