Contents
Research Article
The class semigroup of orders in number fields*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 379-391
-
- Article
- Export citation
Permutability in finite soluble groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-396
-
- Article
- Export citation
Filtrations for q-Young modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-406
-
- Article
- Export citation
Type of blowing-up over a Buchsbaum ring
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-429
-
- Article
- Export citation
Links of prime ideals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-436
-
- Article
- Export citation
The packing measure of self-affine carpets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 437-450
-
- Article
- Export citation
Ordered orbits of the shift, square roots, and the devil's staircase
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-481
-
- Article
- Export citation
On the nilpotence order of β1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-488
-
- Article
- Export citation
Subquotients of UHF C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-500
-
- Article
- Export citation
On Ford isometric spheres in complex hyperbolic space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 501-512
-
- Article
- Export citation
Kähler–Einstein metrics with SU(2) action
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 513-525
-
- Article
- Export citation
Fractal properties of products and projections of measures in ℝd
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-544
-
- Article
- Export citation
On transmission problems for wave propagation in two locally perturbed half-spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-558
-
- Article
- Export citation
Static solutions of the spherically symmetric Vlasov–Einstein system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-570
-
- Article
- Export citation
Fornt matter
PSP volume 115 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
- Export citation
Back matter
PSP volume 115 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b6
-
- Article
-
- You have access
- Export citation
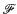 (
(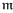 ,
, 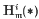 stands for the
stands for the 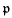 of a Noetherian ring
of a Noetherian ring 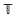 = ℝ/ℤ is ordered if and only if it is contained in a semi-circle
= ℝ/ℤ is ordered if and only if it is contained in a semi-circle 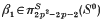 is the first positive even-dimensional element in the stable homotopy groups of spheres. A classical theorem of Nishida[1] states that all elements of positive dimension in the stable homotopy groups of spheres are nilpotent. In fact, Toda [
is the first positive even-dimensional element in the stable homotopy groups of spheres. A classical theorem of Nishida[1] states that all elements of positive dimension in the stable homotopy groups of spheres are nilpotent. In fact, Toda [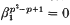 . For
. For 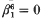 while
while 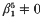 . In [
. In [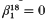 while
while 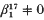 .
.