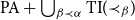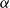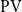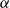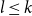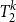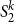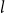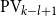1. Introduction
One of the elegant achievements in the history of proof theory is the witnessing techniques connecting the provability of a formula of a certain form to the existence of a computational entity (algorithm (Troelstra Reference Troelstra1998), function (Fairtlough and Wainer Reference Fairtlough and Wainer1998), term in a type theory (Avigad and Feferman Reference Avigad and Feferman1998), etc.) that witnesses the truth of the formula. These connections identify the power of the theories, and they are useful to establish the unprovability of a formula by showing the nonexistence of the corresponding witness. As an example, consider the ordinal analysis as one of the well-known witnessing techniques that among many other things provides a characterization for the provably total recursive functions of some mathematical theories (Buss Reference Buss1994; Fairtlough and Wainer Reference Fairtlough and Wainer1998; Kreisel Reference Kreisel1952). (For a comprehensive high-level explanation, see Rathjen Reference Rathjen1999.) It connects the provability of the totality of a
![]() $\Sigma ^0_1$
-definable function to its time complexity, measured by the proof-theoretic ordinal of the theory. The characterization then leads to some independence results for the formulas in the form
$\Sigma ^0_1$
-definable function to its time complexity, measured by the proof-theoretic ordinal of the theory. The characterization then leads to some independence results for the formulas in the form
![]() $A=\forall x \exists y B(x, y)$
, where
$A=\forall x \exists y B(x, y)$
, where
![]() $B \in \Sigma ^0_1$
is a definition of a function with a faster growth rate and hence higher time complexity than what the theory can actually reach (Fairtlough and Wainer Reference Fairtlough and Wainer1998).
$B \in \Sigma ^0_1$
is a definition of a function with a faster growth rate and hence higher time complexity than what the theory can actually reach (Fairtlough and Wainer Reference Fairtlough and Wainer1998).
There are, however, some settings in which the witnessing techniques and especially the one based on ordinal analysis break down. Sometimes, we are only interested in the formulas with no existential quantifiers to witness (e.g.,
![]() $A=\forall x B(x)$
, where
$A=\forall x B(x)$
, where
![]() $B$
is a quantifier-free formula). Other times, the theory is so weak that even the basics of the witnessing machinery goes beyond the power of the theory. Even working with powerful theories, there can be some problematic situations. For instance, one may be interested in bounded formulas (e.g.,
$B$
is a quantifier-free formula). Other times, the theory is so weak that even the basics of the witnessing machinery goes beyond the power of the theory. Even working with powerful theories, there can be some problematic situations. For instance, one may be interested in bounded formulas (e.g.,
![]() $\forall x \exists y \leq t(x) B(x, y)$
, where all quantifiers in
$\forall x \exists y \leq t(x) B(x, y)$
, where all quantifiers in
![]() $B$
are also bounded) provable in Peano arithmetic, denoted by
$B$
are also bounded) provable in Peano arithmetic, denoted by
![]() $\textrm{PA}$
. Here, what the usual witnessing methods provide is rather weak or even useless. For instance, using ordinal analysis for
$\textrm{PA}$
. Here, what the usual witnessing methods provide is rather weak or even useless. For instance, using ordinal analysis for
![]() $\textrm{PA}$
, the best thing we can learn in the bounded setting is the existence of an algorithm to compute
$\textrm{PA}$
, the best thing we can learn in the bounded setting is the existence of an algorithm to compute
![]() $y$
using a huge amount of time measured by
$y$
using a huge amount of time measured by
![]() $\varepsilon _0$
, the ordinal of the theory. This is much weaker than what we started with, that is, the provability of the totality of the function with a bounded definition. The reason roughly is that the algorithm leads to the existence of the definition
$\varepsilon _0$
, the ordinal of the theory. This is much weaker than what we started with, that is, the provability of the totality of the function with a bounded definition. The reason roughly is that the algorithm leads to the existence of the definition
![]() $\exists w C(x, w, y)$
for the function, where
$\exists w C(x, w, y)$
for the function, where
![]() $w$
encodes the computation and
$w$
encodes the computation and
![]() $\textrm{PA}$
proves
$\textrm{PA}$
proves
![]() $\forall x \exists yw C(x, w, y)$
. However, the computation
$\forall x \exists yw C(x, w, y)$
. However, the computation
![]() $w$
can be huge and hence unbounded by the terms in the language and in this sense proving the totality of a bounded function with a bounded definition is stronger than the existence of such an algorithm.
$w$
can be huge and hence unbounded by the terms in the language and in this sense proving the totality of a bounded function with a bounded definition is stronger than the existence of such an algorithm.
To solve this type of issues and to address both weak theories and low complexity formulas, many new witnessing techniques were designed, from witnessing the universal provable formulas by short propositional proofs (Buss Reference Buss1997; Cook Reference Cook1975; Krajíček and Pudlák Reference Krajíček and Pudlák1990; Paris and Wilkie Reference Paris and Wilkie1981) to witnessing provable bounded formulas in first-order bounded theories of arithmetic in special cases (Buss Reference Buss1986; Buss and Krajíček Reference Buss and Krajíček1994; Krajíček et al. Reference Krajíček, Skelley and Thapen2007) and then in general cases (Beckmann and Buss Reference Beckmann and Buss2010; Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011), using game reductions and different versions of local search problems. A similar technique is also developed for second-order bounded theories of arithmetic (Beckmann and Buss Reference Beckmann and Buss2017, Reference Beckmann and Buss2014; Buss et al. Reference Buss, Krajíček and Takeuti1993; Kołodziejczyk et al. Reference Kołodziejczyk, Nguyen and Thapen2011) and even for Peano arithmetic (Beckmann Reference Beckmann2009). In this paper, we will continue this line of research by providing a general witnessing machinery to witness the low-complexity theorems both in strong and weak theories of arithmetic using a computational entity that we call a flow. Flows are meant to formalize the idea of flowing information and they formally are uniform suitably long sequences of
![]() $\textrm{PV}$
-provable implications between formulas in a suitable class, where
$\textrm{PV}$
-provable implications between formulas in a suitable class, where
![]() $\textrm{PV}$
is Cook’s theory for polynomial time functions. We will work with two different types of flows in this paper, ordinal flows and
$\textrm{PV}$
is Cook’s theory for polynomial time functions. We will work with two different types of flows in this paper, ordinal flows and
![]() $k$
-flows.
$k$
-flows.
Ordinal flows
An ordinal flow is a transfinite uniform sequence of
![]() $\textrm{PV}$
-provable implications between universal formulas. We use ordinal flows to witness low-complexity theorems of the theory
$\textrm{PV}$
-provable implications between universal formulas. We use ordinal flows to witness low-complexity theorems of the theory
![]() $\textrm{PA}+\bigcup _{\beta \prec \alpha } \textrm{TI}({\prec_{\beta}})$
, where
$\textrm{PA}+\bigcup _{\beta \prec \alpha } \textrm{TI}({\prec_{\beta}})$
, where
![]() $\alpha$
is an ordinal with a certain polynomial time representation and
$\alpha$
is an ordinal with a certain polynomial time representation and
![]() $\textrm{TI}({\prec_{\beta}})$
means the transfinite induction up to the ordinal
$\textrm{TI}({\prec_{\beta}})$
means the transfinite induction up to the ordinal
![]() $\beta$
. More precisely, we witness the provability of an implication between two universal formulas in
$\beta$
. More precisely, we witness the provability of an implication between two universal formulas in
![]() $\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
by a uniform sequence of
$\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
by a uniform sequence of
![]() $\textrm{PV}$
-provable implications of length
$\textrm{PV}$
-provable implications of length
![]() $\beta \prec \alpha$
. Using Herbrand’s theorem for
$\beta \prec \alpha$
. Using Herbrand’s theorem for
![]() $\textrm{PV}$
, we push the witnessing further to witness the
$\textrm{PV}$
, we push the witnessing further to witness the
![]() $\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
-provable formulas in the form
$\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
-provable formulas in the form
![]() $A=\forall \bar{x}\exists \bar{y} B(\bar{x},\bar{y})$
, where
$A=\forall \bar{x}\exists \bar{y} B(\bar{x},\bar{y})$
, where
![]() $B$
is a polynomial time computable predicate by an algorithm to compute
$B$
is a polynomial time computable predicate by an algorithm to compute
![]() $\bar{y}$
by a sequence of
$\bar{y}$
by a sequence of
![]() $\textrm{PV}$
-provable polynomial time modifications on an initial polynomial time value, where the computational steps are indexed by the ordinals below
$\textrm{PV}$
-provable polynomial time modifications on an initial polynomial time value, where the computational steps are indexed by the ordinals below
![]() $\alpha$
, decreasing by the modifications. Our result generalizes the main theorem of Beckmann (Reference Beckmann2009) that developed a similar characterization for
$\alpha$
, decreasing by the modifications. Our result generalizes the main theorem of Beckmann (Reference Beckmann2009) that developed a similar characterization for
![]() $\textrm{PA}$
. However, as we will explain below, even for that special case, we use a simpler and easier to generalize methodology.
$\textrm{PA}$
. However, as we will explain below, even for that special case, we use a simpler and easier to generalize methodology.
To compare our result to the existing literature on ordinal analysis, it is important to focus on the role of the polynomial time computable functions and the theory
![]() $\textrm{PV}$
in our contribution. First, note that changing the polynomial time functions and
$\textrm{PV}$
in our contribution. First, note that changing the polynomial time functions and
![]() $\textrm{PV}$
in our characterization to the elementary or primitive recursive functions and
$\textrm{PV}$
in our characterization to the elementary or primitive recursive functions and
![]() $\textrm{ERA}$
or
$\textrm{ERA}$
or
![]() $\textrm{PRA}$
, respectively, makes the characterization an easy consequence of the known facts in the ordinal analysis literature. For instance, one can use the powerful witnessing theorems in Friedman and Sheard (Reference Friedman and Sheard1995), Avigad (Reference Avigad2002) or the interesting algebraic presentation of the ordinals in Beklemishev (Reference Beklemishev2004). What is not trivial, though, is providing a low-complexity version suitable to witness the low-complexity theorems of arithmetic. To reach such a version, we have two options. The first, as followed in the above-mentioned paper (Beckmann Reference Beckmann2009), rewrites the continuous cut elimination technique (Buchholz Reference Buchholz1991, Reference Buchholz1997), replacing all primitive recursive functions by more careful polynomial time computable operations (Beckmann et al. Reference Beckmann, Pollett and Buss2003). The second as an indirect approach uses the known results in ordinal analysis as a black-box and rewitness them in a feasible manner to circumvent redoing the tedious ordinal analysis argument. This option is what we follow in the present paper. More precisely, we first use the refined ordinal analysis in Friedman and Sheard (Reference Friedman and Sheard1995) to show that a
$\textrm{PRA}$
, respectively, makes the characterization an easy consequence of the known facts in the ordinal analysis literature. For instance, one can use the powerful witnessing theorems in Friedman and Sheard (Reference Friedman and Sheard1995), Avigad (Reference Avigad2002) or the interesting algebraic presentation of the ordinals in Beklemishev (Reference Beklemishev2004). What is not trivial, though, is providing a low-complexity version suitable to witness the low-complexity theorems of arithmetic. To reach such a version, we have two options. The first, as followed in the above-mentioned paper (Beckmann Reference Beckmann2009), rewrites the continuous cut elimination technique (Buchholz Reference Buchholz1991, Reference Buchholz1997), replacing all primitive recursive functions by more careful polynomial time computable operations (Beckmann et al. Reference Beckmann, Pollett and Buss2003). The second as an indirect approach uses the known results in ordinal analysis as a black-box and rewitness them in a feasible manner to circumvent redoing the tedious ordinal analysis argument. This option is what we follow in the present paper. More precisely, we first use the refined ordinal analysis in Friedman and Sheard (Reference Friedman and Sheard1995) to show that a
![]() $\Pi ^0_2$
-formula is provable in the theory
$\Pi ^0_2$
-formula is provable in the theory
![]() $\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
iff it is provable in an extension of
$\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
iff it is provable in an extension of
![]() $\textrm{PRA}$
with a weak form of transfinite induction. Then, using a suitable polynomial time representation for the ordinals below
$\textrm{PRA}$
with a weak form of transfinite induction. Then, using a suitable polynomial time representation for the ordinals below
![]() $\alpha$
, we will transform a proof in the weaker theory to a sequence of
$\alpha$
, we will transform a proof in the weaker theory to a sequence of
![]() $\textrm{PV}$
-provable polynomial time modifications described above. Our technique of using ordinally long sequence of easy modifications is similar to what used in Avigad (Reference Avigad2002), although its machinery has a more model-theoretic character and also implements the ordinal analysis from the scratch. Roughly speaking, Avigad (Reference Avigad2002) provides a similar witnessing theorem using elementary functions rather than polynomial time functions in its ordinal flows. However, to have a verifiablity criterion, it insists on having the whole witnessing process provable inside the meta-theory
$\textrm{PV}$
-provable polynomial time modifications described above. Our technique of using ordinally long sequence of easy modifications is similar to what used in Avigad (Reference Avigad2002), although its machinery has a more model-theoretic character and also implements the ordinal analysis from the scratch. Roughly speaking, Avigad (Reference Avigad2002) provides a similar witnessing theorem using elementary functions rather than polynomial time functions in its ordinal flows. However, to have a verifiablity criterion, it insists on having the whole witnessing process provable inside the meta-theory
![]() $\textrm{PRA}$
. The witnessing machinery of Avigad (Reference Avigad2002) cannot be directly used to prove the low-complexity version we are interested in here. The reason is its use of
$\textrm{PRA}$
. The witnessing machinery of Avigad (Reference Avigad2002) cannot be directly used to prove the low-complexity version we are interested in here. The reason is its use of
![]() $\textrm{PRA}$
-formalized Herbrand’s theorem for first-order logic that uses cut elimination, and it is extremely costly to be directly formalizable in
$\textrm{PRA}$
-formalized Herbrand’s theorem for first-order logic that uses cut elimination, and it is extremely costly to be directly formalizable in
![]() $\textrm{PV}$
. To solve the issue, as Avigad (Reference Avigad2002) also suggests, one must witness the Herbrand’s theorem part by a sequence of
$\textrm{PV}$
. To solve the issue, as Avigad (Reference Avigad2002) also suggests, one must witness the Herbrand’s theorem part by a sequence of
![]() $\textrm{PV}$
-verifiable modifications or equivalently witness the first-order logic by such modifications, directly. This is one of the things we do in the present paper. Therefore, although our work is inspired by Beckmann (Reference Beckmann2009) and the witnessing theorems in bounded arithmetic and hence its technique was developed independent from Avigad (Reference Avigad2002), one can interpret our contribution as a generalization of Avigad (Reference Avigad2002) making its machinery applicable even in the low-complexity settings.
$\textrm{PV}$
-verifiable modifications or equivalently witness the first-order logic by such modifications, directly. This is one of the things we do in the present paper. Therefore, although our work is inspired by Beckmann (Reference Beckmann2009) and the witnessing theorems in bounded arithmetic and hence its technique was developed independent from Avigad (Reference Avigad2002), one can interpret our contribution as a generalization of Avigad (Reference Avigad2002) making its machinery applicable even in the low-complexity settings.
 $k$
-flows
$k$
-flows
A (polynomial)
![]() $k$
-flow is a uniform (polynomially) exponentially long sequence of
$k$
-flow is a uniform (polynomially) exponentially long sequence of
![]() $\textrm{PV}$
-provable implications between
$\textrm{PV}$
-provable implications between
![]() $\hat{\Pi }^b_k$
-formulas. Recall that
$\hat{\Pi }^b_k$
-formulas. Recall that
![]() $\hat{\Pi }^b_k$
- (
$\hat{\Pi }^b_k$
- (
![]() $\hat{\Sigma }^b_k$
-formulas) are roughly the formulas with
$\hat{\Sigma }^b_k$
-formulas) are roughly the formulas with
![]() $k$
-many bounded quantifier blocks starting with a universal (existential) block and followed by a quantifier-free formula over the language
$k$
-many bounded quantifier blocks starting with a universal (existential) block and followed by a quantifier-free formula over the language
![]() $\mathcal{L}_{\textrm{PV}}$
that has a term for any polynomial time computable function. We will witness the provability of an implication between
$\mathcal{L}_{\textrm{PV}}$
that has a term for any polynomial time computable function. We will witness the provability of an implication between
![]() $\hat{\Pi }^b_k$
-formulas in
$\hat{\Pi }^b_k$
-formulas in
![]() $T^k_2$
(resp.
$T^k_2$
(resp.
![]() $S^k_2$
) by a
$S^k_2$
) by a
![]() $k$
-flow (resp. polynomial
$k$
-flow (resp. polynomial
![]() $k$
-flow). To push the witnessing further, we can use Herbrand’s theorem again for the universal theory
$k$
-flow). To push the witnessing further, we can use Herbrand’s theorem again for the universal theory
![]() $\textrm{PV}$
. However, this time the formulas are in
$\textrm{PV}$
. However, this time the formulas are in
![]() $\hat{\Pi }^b_k$
and hence we have
$\hat{\Pi }^b_k$
and hence we have
![]() $k$
-many layers of quantifier to peel off. To control the number of layers, we intend to remove, and we will follow a relative approach. We fix a number
$k$
-many layers of quantifier to peel off. To control the number of layers, we intend to remove, and we will follow a relative approach. We fix a number
![]() $l \leq k$
and only peel off the outmost
$l \leq k$
and only peel off the outmost
![]() $l$
many quantifier blocks. More precisely, we first move the
$l$
many quantifier blocks. More precisely, we first move the
![]() $\textrm{PV}$
-provable implications from
$\textrm{PV}$
-provable implications from
![]() $\textrm{PV}$
to
$\textrm{PV}$
to
![]() $\textrm{PV}_{k-l+1}$
, a universal theory for the functions in the
$\textrm{PV}_{k-l+1}$
, a universal theory for the functions in the
![]() $(k-l+1)$
-th level of the polynomial hierarchy. This way we can pretend that all the formulas in
$(k-l+1)$
-th level of the polynomial hierarchy. This way we can pretend that all the formulas in
![]() $\hat{\Sigma }^b_{k-l} \cup \hat{\Pi }^b_{k-l}$
are quantifier-free. Therefore, only
$\hat{\Sigma }^b_{k-l} \cup \hat{\Pi }^b_{k-l}$
are quantifier-free. Therefore, only
![]() $l$
many quantifier blocks are left to witness. Using Herbrand’s theorem for the theory
$l$
many quantifier blocks are left to witness. Using Herbrand’s theorem for the theory
![]() $\textrm{PV}_{k-l+1}$
and reading any quantifier-free formula in the language of
$\textrm{PV}_{k-l+1}$
and reading any quantifier-free formula in the language of
![]() $\textrm{PV}_{k-l+1}$
as an
$\textrm{PV}_{k-l+1}$
as an
![]() $l$
-turn game (Skelley and Thapen Reference Skelley and Thapen2011), we can then witness any
$l$
-turn game (Skelley and Thapen Reference Skelley and Thapen2011), we can then witness any
![]() $\textrm{PV}$
-provable implication by an explicit
$\textrm{PV}$
-provable implication by an explicit
![]() $\textrm{PV}_{k-l+1}$
-verifiable reduction between
$\textrm{PV}_{k-l+1}$
-verifiable reduction between
![]() $l$
-turn games. These reductions are somewhat nondeterministic mapping their input values to some possible instances, where one of the options may work, (see the second part in Theorem 2 to see what we mean by nondeterminism in this context). Finally, using these reductions, we show that a formula in the form
$l$
-turn games. These reductions are somewhat nondeterministic mapping their input values to some possible instances, where one of the options may work, (see the second part in Theorem 2 to see what we mean by nondeterminism in this context). Finally, using these reductions, we show that a formula in the form
![]() $\forall \bar{x} \exists y \leq r(\bar{x}) B(\bar{x}, y)$
, where
$\forall \bar{x} \exists y \leq r(\bar{x}) B(\bar{x}, y)$
, where
![]() $B \in \hat{\Sigma }^b_{k-l} \cup \hat{\Pi }^b_{k-l}$
is provable in
$B \in \hat{\Sigma }^b_{k-l} \cup \hat{\Pi }^b_{k-l}$
is provable in
![]() $T^k_2$
(resp.
$T^k_2$
(resp.
![]() $S^k_2$
) iff there is a uniform (polynomially) exponentially long sequence of
$S^k_2$
) iff there is a uniform (polynomially) exponentially long sequence of
![]() $\textrm{PV}_{k-l+1}$
-verifiable reductions between
$\textrm{PV}_{k-l+1}$
-verifiable reductions between
![]() $l$
-turn games, starting from an explicit
$l$
-turn games, starting from an explicit
![]() $\textrm{PV}_{k-l+1}$
-verifiable winning strategy for the first game. We will only spell out the details for
$\textrm{PV}_{k-l+1}$
-verifiable winning strategy for the first game. We will only spell out the details for
![]() $l=1,2$
. For
$l=1,2$
. For
![]() $l=1$
, we show that our witnessing theorem reproves some of the well-known witnessing theorems for
$l=1$
, we show that our witnessing theorem reproves some of the well-known witnessing theorems for
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
including the usual witnessing of
$T^k_2$
including the usual witnessing of
![]() $\hat{\Sigma }^b_k$
-definable functions of
$\hat{\Sigma }^b_k$
-definable functions of
![]() $S^k_2$
by
$S^k_2$
by
![]() $\square ^p_k$
-functions (Buss Reference Buss1986) and
$\square ^p_k$
-functions (Buss Reference Buss1986) and
![]() $\hat{\Sigma }^b_1$
-definable multifunctions of
$\hat{\Sigma }^b_1$
-definable multifunctions of
![]() $T^1_2$
by polynomial local search problems Buss and Krajíček (1994). For
$T^1_2$
by polynomial local search problems Buss and Krajíček (1994). For
![]() $l=2$
, we provide new witnessing theorems. For
$l=2$
, we provide new witnessing theorems. For
![]() $T^k_2$
, there are other witnessing methods providing similar characterizations as ours based on better (i.e., deterministic) game reductions (Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011). The theory of flows can also prove these stronger characterizations. However, it needs to work with more involved notions of a
$T^k_2$
, there are other witnessing methods providing similar characterizations as ours based on better (i.e., deterministic) game reductions (Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011). The theory of flows can also prove these stronger characterizations. However, it needs to work with more involved notions of a
![]() $k$
-flow than what we have here. We leave such investigations to another paper. For
$k$
-flow than what we have here. We leave such investigations to another paper. For
![]() $S^k_2$
, however, our result, to the best of our knowledge, is the only characterization in the same style of the original witnessing theorems (Buss Reference Buss1986) that reduce the provability in
$S^k_2$
, however, our result, to the best of our knowledge, is the only characterization in the same style of the original witnessing theorems (Buss Reference Buss1986) that reduce the provability in
![]() $S^k_2$
to a polynomially long sequence of feasible modifications. Of course, one can use the conservativity of
$S^k_2$
to a polynomially long sequence of feasible modifications. Of course, one can use the conservativity of
![]() $S^k_2$
over
$S^k_2$
over
![]() $T^{k-1}_2$
for
$T^{k-1}_2$
for
![]() $\hat{\Sigma }^b_{k}$
-formulas and then using the witnessing for
$\hat{\Sigma }^b_{k}$
-formulas and then using the witnessing for
![]() $T^{k-1}_2$
by the deterministic game reductions (Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011) or any other characterization (Beckmann and Buss 2009, 2010), find a witnessing theorem for
$T^{k-1}_2$
by the deterministic game reductions (Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011) or any other characterization (Beckmann and Buss 2009, 2010), find a witnessing theorem for
![]() $S^k_2$
. Using this approach, the characterizations provide an exponentially long sequence of deterministic reductions while we provide a polynomially long sequence of more complex nondeterministic reductions. These two different approaches can be seen as an instance of the usual phenomenon of simulating the huge power of the deterministic exponential time with polynomial time nondeterminism, where the latter, if possible, is more informative than the former.
$S^k_2$
. Using this approach, the characterizations provide an exponentially long sequence of deterministic reductions while we provide a polynomially long sequence of more complex nondeterministic reductions. These two different approaches can be seen as an instance of the usual phenomenon of simulating the huge power of the deterministic exponential time with polynomial time nondeterminism, where the latter, if possible, is more informative than the former.
Finally, to compare our witnessing method to the rich literature on witnessing theorems in bounded arithmetic, let us emphasize two points that we find unique to our characterization. First, unlike the methods used in Buss and Krajíček (Reference Buss and Krajíček1994), Krajíček et al. (Reference Krajíček, Skelley and Thapen2007), Skelley and Thapen (Reference Skelley and Thapen2011), Thapen (Reference Thapen2011), Beckmann and Buss (2009, 2010), our machinery is sufficiently general to directly witness bounded theories arising from practically any type of bounded induction Akbar Tabatabai (Reference Tabatabai2018). For instance, for any
![]() $m \geq 2$
, consider the language
$m \geq 2$
, consider the language
![]() $\mathcal{L}_{\textrm{PV}} \cup \{\#_m\}$
, where
$\mathcal{L}_{\textrm{PV}} \cup \{\#_m\}$
, where
![]() $x\#_2 y=2^{|x||y|}$
and
$x\#_2 y=2^{|x||y|}$
and
![]() $x \#_{i+1} y=2^{|x| \#_i |y|}$
and define the class
$x \#_{i+1} y=2^{|x| \#_i |y|}$
and define the class
![]() $\hat{\Pi }^b_k(\#_m)$
and the theory
$\hat{\Pi }^b_k(\#_m)$
and the theory
![]() $\textrm{PV}(\#_m)$
over the new language similar to
$\textrm{PV}(\#_m)$
over the new language similar to
![]() $\hat{\Pi }^b_k$
and
$\hat{\Pi }^b_k$
and
![]() $\textrm{PV}$
over
$\textrm{PV}$
over
![]() $\mathcal{L}_{\textrm{PV}}$
. Now, for any
$\mathcal{L}_{\textrm{PV}}$
. Now, for any
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $m \geq n+2$
, and
$m \geq n+2$
, and
![]() $k \geq 1$
, define the theory
$k \geq 1$
, define the theory
![]() $R^k_{m, n}$
as the extension of a basic universal theory to handle the function symbols, by the induction axiom
$R^k_{m, n}$
as the extension of a basic universal theory to handle the function symbols, by the induction axiom
where
![]() $A \in \hat{\Pi }^b_k(\#_m)$
,
$A \in \hat{\Pi }^b_k(\#_m)$
,
![]() $|x|_0=x$
, and
$|x|_0=x$
, and
![]() $|x|_{j+1}=||x|_j|$
. It is easy to imitate our technique in the present paper to witness
$|x|_{j+1}=||x|_j|$
. It is easy to imitate our technique in the present paper to witness
![]() $R^k_{m,n}$
-provable implications between
$R^k_{m,n}$
-provable implications between
![]() $\hat{\Pi }^b_k(\#_m)$
-formulas by a uniform sequence of
$\hat{\Pi }^b_k(\#_m)$
-formulas by a uniform sequence of
![]() $\textrm{PV}(\#_m)$
-provable implications between
$\textrm{PV}(\#_m)$
-provable implications between
![]() $\hat{\Pi }^b_k(\#_m)$
-formulas with the length
$\hat{\Pi }^b_k(\#_m)$
-formulas with the length
![]() $|t|_n$
, for some term
$|t|_n$
, for some term
![]() $t$
. This can be even more generalized to any type of induction satisfying some basic properties Akbar Tabatabai (Reference Tabatabai2018).
$t$
. This can be even more generalized to any type of induction satisfying some basic properties Akbar Tabatabai (Reference Tabatabai2018).
The second point is that the length of our witnessing flows honestly reflects the type of the induction we use. For instance, for
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
, we use polynomially long and exponentially long
$T^k_2$
, we use polynomially long and exponentially long
![]() $k$
-flows, respectively, and more generally, in
$k$
-flows, respectively, and more generally, in
![]() $R^k_{m, n}$
where the induction is up to
$R^k_{m, n}$
where the induction is up to
![]() $|x|_n$
, the length of the witnessing flow is
$|x|_n$
, the length of the witnessing flow is
![]() $|t|_n$
, for some term
$|t|_n$
, for some term
![]() $t$
, see Akbar Tabatabai (Reference Tabatabai2018). This honest correspondence is not typical with the above-mentioned characterizations. For instance, the polynomially long adaptation of the known characterizations for
$t$
, see Akbar Tabatabai (Reference Tabatabai2018). This honest correspondence is not typical with the above-mentioned characterizations. For instance, the polynomially long adaptation of the known characterizations for
![]() $T^k_2$
(Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011), that is, polynomially long sequence of
$T^k_2$
(Skelley and Thapen Reference Skelley and Thapen2011; Thapen Reference Thapen2011), that is, polynomially long sequence of
![]() $\textrm{PV}$
-verifiable deterministic reductions between
$\textrm{PV}$
-verifiable deterministic reductions between
![]() $k$
-turn games, does not witness
$k$
-turn games, does not witness
![]() $S^k_2$
-provable implications. The reason is that any polynomially long iteration of a deterministic reduction is again a deterministic reduction itself. Therefore, if such a witnessing theorem holds, one can witness the implications in
$S^k_2$
-provable implications. The reason is that any polynomially long iteration of a deterministic reduction is again a deterministic reduction itself. Therefore, if such a witnessing theorem holds, one can witness the implications in
![]() $S^k_2$
between
$S^k_2$
between
![]() $\hat{\Pi }^b_k$
-formulas by a polynomially long sequence of reductions and hence only one reduction. Thus, the
$\hat{\Pi }^b_k$
-formulas by a polynomially long sequence of reductions and hence only one reduction. Thus, the
![]() $\hat{\Sigma }^b_k$
-definable functions of
$\hat{\Sigma }^b_k$
-definable functions of
![]() $S^k_2$
must be all polynomial time computable and as all the functions in
$S^k_2$
must be all polynomial time computable and as all the functions in
![]() $\square ^p_k$
are
$\square ^p_k$
are
![]() $\hat{\Sigma }^b_k$
-definable in
$\hat{\Sigma }^b_k$
-definable in
![]() $S^k_2$
, the polynomial hierarchy must collapse. This simple observation shows that the nondeterminism we use in our reductions is essential to have an honest characterization. Moreover, it shows that our characterization for
$S^k_2$
, the polynomial hierarchy must collapse. This simple observation shows that the nondeterminism we use in our reductions is essential to have an honest characterization. Moreover, it shows that our characterization for
![]() $S^k_2$
is not a simple consequence of the methodologies used for
$S^k_2$
is not a simple consequence of the methodologies used for
![]() $T^k_2$
in Skelley and Thapen (Reference Skelley and Thapen2011), Thapen (Reference Thapen2011) or even in Beckmann and Buss (2009, 2010).
$T^k_2$
in Skelley and Thapen (Reference Skelley and Thapen2011), Thapen (Reference Thapen2011) or even in Beckmann and Buss (2009, 2010).
Here is the structure of the paper. In Section 2, we recall the basic definitions of different languages and arithmetical systems we use in this paper. In Section 3, we introduce our version of polynomial time ordinal representation and we recall the one introduced in Beckmann et al. (Reference Beckmann, Pollett and Buss2003) for
![]() $\varepsilon _0$
. In Section 4, we present ordinal flows and the witnessing technique to reduce the provability of the low complexity statements in the theory
$\varepsilon _0$
. In Section 4, we present ordinal flows and the witnessing technique to reduce the provability of the low complexity statements in the theory
![]() $\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
. Finally, in Section 5, we introduce
$\textrm{PA}+\bigcup _{\beta \prec \alpha }\textrm{TI}({\prec_{\beta}})$
. Finally, in Section 5, we introduce
![]() $k$
-flows to witness the provability of the low complexity statements in the theories
$k$
-flows to witness the provability of the low complexity statements in the theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
.
$T^k_2$
.
2. Preliminaries
For any first-order language
![]() $\mathcal{L}$
, by an
$\mathcal{L}$
, by an
![]() $\mathcal{L}$
-formula, we mean any expression constructible by the connectives
$\mathcal{L}$
-formula, we mean any expression constructible by the connectives
![]() $\{\wedge, \vee, \forall, \exists \}$
from the atomic formulas (including
$\{\wedge, \vee, \forall, \exists \}$
from the atomic formulas (including
![]() $\bot$
and
$\bot$
and
![]() $\top$
) and their negations. The formula
$\top$
) and their negations. The formula
![]() $\neg A$
is defined via de Morgan laws and
$\neg A$
is defined via de Morgan laws and
![]() $A \to B$
is an abbreviation for
$A \to B$
is an abbreviation for
![]() $\neg A \vee B$
. By an
$\neg A \vee B$
. By an
![]() $\mathcal{L}$
-term, we simply mean a term in the language
$\mathcal{L}$
-term, we simply mean a term in the language
![]() $\mathcal{L}$
. By
$\mathcal{L}$
. By
![]() $\bar{t}$
, we mean a sequence of terms in the language and
$\bar{t}$
, we mean a sequence of terms in the language and
![]() $\bar{x}$
means a sequence of variables.
$\bar{x}$
means a sequence of variables.
To introduce the system
![]() $\textrm{PV}$
, let us recall Cobham’s machine-independent characterization of polynomial-time computable (ptime, for short) functions (Cobham Reference Cobham1965). It states that a function is ptime iff it is constructible from certain basic functions by composition and a weak sort of recursion called the bounded recursion on notation. Any such construction provides an algorithm to compute the corresponding ptime function. Let
$\textrm{PV}$
, let us recall Cobham’s machine-independent characterization of polynomial-time computable (ptime, for short) functions (Cobham Reference Cobham1965). It states that a function is ptime iff it is constructible from certain basic functions by composition and a weak sort of recursion called the bounded recursion on notation. Any such construction provides an algorithm to compute the corresponding ptime function. Let
![]() $\mathcal{L}_{\textrm{PV}}$
be a first-order language with a function symbol for any such algorithm. In Cook (Reference Cook1975), Cook introduced an equational theory over the language
$\mathcal{L}_{\textrm{PV}}$
be a first-order language with a function symbol for any such algorithm. In Cook (Reference Cook1975), Cook introduced an equational theory over the language
![]() $\mathcal{L}_{\textrm{PV}}$
to reason about ptime functions. The theory essentially consists of the defining axioms for the function symbols together with a sort of induction rule. Later, a conservative first-order extension of
$\mathcal{L}_{\textrm{PV}}$
to reason about ptime functions. The theory essentially consists of the defining axioms for the function symbols together with a sort of induction rule. Later, a conservative first-order extension of
![]() $\textrm{PV}$
, denoted by
$\textrm{PV}$
, denoted by
![]() $\textrm{PV}_1$
, was introduced by Krajíček et al. (Reference Krajíček, Pudlák and Takeuti1991). The theory has the polynomial induction axiom scheme denoted by
$\textrm{PV}_1$
, was introduced by Krajíček et al. (Reference Krajíček, Pudlák and Takeuti1991). The theory has the polynomial induction axiom scheme denoted by
![]() $\textrm{PInd}$
$\textrm{PInd}$
for any quantifier-free formula
![]() $A(x)$
and is universally axiomatizable (Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991). In this paper, we will only use the theory
$A(x)$
and is universally axiomatizable (Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991). In this paper, we will only use the theory
![]() $\textrm{PV}_1$
and not
$\textrm{PV}_1$
and not
![]() $\textrm{PV}$
. Therefore, by abuse of notation, we will use the name
$\textrm{PV}$
. Therefore, by abuse of notation, we will use the name
![]() $\textrm{PV}$
to denote its first-order extension
$\textrm{PV}$
to denote its first-order extension
![]() $\textrm{PV}_1$
.
$\textrm{PV}_1$
.
In any language extending
![]() $\mathcal{L}_{\textrm{PV}}$
, by a bounded quantifier, we mean a quantifier in the form
$\mathcal{L}_{\textrm{PV}}$
, by a bounded quantifier, we mean a quantifier in the form
![]() $\forall x (x \leq t \to A(x))$
or
$\forall x (x \leq t \to A(x))$
or
![]() $\exists x (x \leq t \wedge A(x))$
, abbreviated by
$\exists x (x \leq t \wedge A(x))$
, abbreviated by
![]() $\forall x \leq t \, A(x)$
and
$\forall x \leq t \, A(x)$
and
![]() $\exists x \leq t \, A(x)$
, respectively. For any sequence of variables
$\exists x \leq t \, A(x)$
, respectively. For any sequence of variables
![]() $\bar{x}=(x_1, \ldots, x_n)$
and terms
$\bar{x}=(x_1, \ldots, x_n)$
and terms
![]() $\bar{t}=(t_1, \ldots, t_n)$
, by
$\bar{t}=(t_1, \ldots, t_n)$
, by
![]() $Q \bar{x} \leq \bar{t} \, A(\bar{x})$
, we mean
$Q \bar{x} \leq \bar{t} \, A(\bar{x})$
, we mean
![]() $Q x_1 \leq t_1 Q x_2 \leq t_2 \ldots A(x_1, \ldots, x_n)$
, for any
$Q x_1 \leq t_1 Q x_2 \leq t_2 \ldots A(x_1, \ldots, x_n)$
, for any
![]() $Q \in \{\forall, \exists \}$
.
$Q \in \{\forall, \exists \}$
.
By recursion on
![]() $k$
, define the classes
$k$
, define the classes
![]() $\hat{\Sigma }^b_k$
and
$\hat{\Sigma }^b_k$
and
![]() $\hat{\Pi }^b_k$
of
$\hat{\Pi }^b_k$
of
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas in the following way:
$\mathcal{L}_{\textrm{PV}}$
-formulas in the following way:
-
•
 $\hat{\Pi }^b_0=\hat{\Sigma }^b_0$
is the class of all quantifier-free formulas,
$\hat{\Pi }^b_0=\hat{\Sigma }^b_0$
is the class of all quantifier-free formulas, -
•
 $\hat{\Sigma }_k^b \subseteq \hat{\Sigma }^b_{k+1}$
and
$\hat{\Sigma }_k^b \subseteq \hat{\Sigma }^b_{k+1}$
and
 $\hat{\Pi }^b_k \subseteq \hat{\Pi }^b_{k+1}$
,
$\hat{\Pi }^b_k \subseteq \hat{\Pi }^b_{k+1}$
, -
•
 $\hat{\Pi }^b_k$
and
$\hat{\Pi }^b_k$
and
 $\hat{\Sigma }^b_k$
are closed under conjunction and disjunction,
$\hat{\Sigma }^b_k$
are closed under conjunction and disjunction, -
• If
 $B(x) \in \hat{\Sigma }^b_k$
, then
$B(x) \in \hat{\Sigma }^b_k$
, then
 $\exists x \leq t \; B(x) \in \hat{\Sigma }^b_k$
and
$\exists x \leq t \; B(x) \in \hat{\Sigma }^b_k$
and
 $\forall x \leq t \; B(x) \in \hat{\Pi }^b_{k+1}$
and
$\forall x \leq t \; B(x) \in \hat{\Pi }^b_{k+1}$
and -
• If
 $B(x) \in \hat{\Pi }^b_k$
, then
$B(x) \in \hat{\Pi }^b_k$
, then
 $\forall x \leq t \; B(x) \in \hat{\Pi }^b_k$
and
$\forall x \leq t \; B(x) \in \hat{\Pi }^b_k$
and
 $\forall x \leq t \; B(x) \in \hat{\Sigma }^b_{k+1}$
.
$\forall x \leq t \; B(x) \in \hat{\Sigma }^b_{k+1}$
.
Define
![]() $\hat{\Sigma }^b_{\infty }=\hat{\Pi }^b_{\infty }$
as
$\hat{\Sigma }^b_{\infty }=\hat{\Pi }^b_{\infty }$
as
![]() $\bigcup _{k=0}^{\infty } \hat{\Sigma }^b_{k}$
that is the same as
$\bigcup _{k=0}^{\infty } \hat{\Sigma }^b_{k}$
that is the same as
![]() $\bigcup _{k=0}^{\infty } \hat{\Pi }^b_{k}$
. For the sake of simplicity, we suppressed the free variables in our notation in the above definition while they are also allowed to be used in the formulas.
$\bigcup _{k=0}^{\infty } \hat{\Pi }^b_{k}$
. For the sake of simplicity, we suppressed the free variables in our notation in the above definition while they are also allowed to be used in the formulas.
By the axiom scheme
![]() $\hat{\Pi }^b_k-\textrm{PInd}$
, we mean
$\hat{\Pi }^b_k-\textrm{PInd}$
, we mean
for any
![]() $A \in \hat{\Pi }^b_k$
and by
$A \in \hat{\Pi }^b_k$
and by
![]() $\hat{\Pi }^b_{k}-\textrm{Ind}$
, we mean
$\hat{\Pi }^b_{k}-\textrm{Ind}$
, we mean
for
![]() $A \in \hat{\Pi }^b_k$
. The schemes
$A \in \hat{\Pi }^b_k$
. The schemes
![]() $\hat{\Sigma }^b_{k}-\textrm{PInd}$
and
$\hat{\Sigma }^b_{k}-\textrm{PInd}$
and
![]() $\hat{\Sigma }^b_{k}-\textrm{Ind}$
are defined similarly. For any
$\hat{\Sigma }^b_{k}-\textrm{Ind}$
are defined similarly. For any
![]() $k \geq 1$
, define the theories
$k \geq 1$
, define the theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
as
$T^k_2$
as
![]() $\textrm{PV}+\hat{\Pi }^b_k-\textrm{PInd}$
and
$\textrm{PV}+\hat{\Pi }^b_k-\textrm{PInd}$
and
![]() $\textrm{PV}+\hat{\Pi }^b_k-\textrm{Ind}$
, respectively. It is known that
$\textrm{PV}+\hat{\Pi }^b_k-\textrm{Ind}$
, respectively. It is known that
![]() $S^k_2$
(resp.,
$S^k_2$
(resp.,
![]() $T^k_2$
) proves
$T^k_2$
) proves
![]() $\hat{\Sigma }^b_{k}-\textrm{PInd}$
(resp.,
$\hat{\Sigma }^b_{k}-\textrm{PInd}$
(resp.,
![]() $\hat{\Sigma }^b_{k}-\textrm{Ind}$
). It is also useful to mention that the following axiom scheme, denoted by
$\hat{\Sigma }^b_{k}-\textrm{Ind}$
). It is also useful to mention that the following axiom scheme, denoted by
![]() $\hat{\Pi }^b_k-\textrm{LInd}$
$\hat{\Pi }^b_k-\textrm{LInd}$
where
![]() $A \in \hat{\Pi }^b_k$
, is provable in
$A \in \hat{\Pi }^b_k$
, is provable in
![]() $S^k_2$
. The same also holds for
$S^k_2$
. The same also holds for
![]() $\hat{\Sigma }^b_k-\textrm{LInd}$
, where we replace
$\hat{\Sigma }^b_k-\textrm{LInd}$
, where we replace
![]() $\hat{\Pi }^b_k$
by
$\hat{\Pi }^b_k$
by
![]() $\hat{\Sigma }^b_k$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). The following theorem is true for theories
$\hat{\Sigma }^b_k$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). The following theorem is true for theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
Krajíček (Reference Krajíček1995).
$T^k_2$
Krajíček (Reference Krajíček1995).
Theorem.
(Parikh) Let
![]() $T$
be either
$T$
be either
![]() $S^k_2$
or
$S^k_2$
or
![]() $T^k_2$
, for some
$T^k_2$
, for some
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $A(\bar{x}, y)$
be an
$A(\bar{x}, y)$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-formula in
$\mathcal{L}_{\textrm{PV}}$
-formula in
![]() $\hat{\Sigma }^b_{\infty }$
. Then, if
$\hat{\Sigma }^b_{\infty }$
. Then, if
![]() $T \vdash \forall \bar{x} \exists y A(\bar{x}, y)$
, then there exists an
$T \vdash \forall \bar{x} \exists y A(\bar{x}, y)$
, then there exists an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $t(\bar{x})$
such that
$t(\bar{x})$
such that
![]() $T \vdash \forall \bar{x} \exists y \leq t(\bar{x}) A(\bar{x}, y)$
.
$T \vdash \forall \bar{x} \exists y \leq t(\bar{x}) A(\bar{x}, y)$
.
It is possible to define a universal theory for any level in the polynomial hierarchy, similar to what
![]() $\textrm{PV}_1$
does for the polynomial time computable functions. More precisely, for any
$\textrm{PV}_1$
does for the polynomial time computable functions. More precisely, for any
![]() $k \geq 2$
, one can define a universal theory
$k \geq 2$
, one can define a universal theory
![]() $\textrm{PV}_{k}$
over an extended language
$\textrm{PV}_{k}$
over an extended language
![]() $\mathcal{L}_{\textrm{PV}_k}$
that has a term for any function in the
$\mathcal{L}_{\textrm{PV}_k}$
that has a term for any function in the
![]() $k$
th level of the polynomial hierarchy, denoted by
$k$
th level of the polynomial hierarchy, denoted by
![]() $\square ^p_k$
(Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991). We do not spell out the details of these theories. The only thing we need to know is that
$\square ^p_k$
(Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991). We do not spell out the details of these theories. The only thing we need to know is that
![]() $\textrm{PV}_k$
has an explicit term for the characteristic functions of
$\textrm{PV}_k$
has an explicit term for the characteristic functions of
![]() $\hat{\Sigma }^b_k$
-formula and its term construction allows defining functions by bounded recursion on notation (Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991; Krajíček Reference Krajíček1995). As
$\hat{\Sigma }^b_k$
-formula and its term construction allows defining functions by bounded recursion on notation (Krajíček et al. Reference Krajíček, Pudlák and Takeuti1991; Krajíček Reference Krajíček1995). As
![]() $\textrm{PV}_k$
is universal, it enjoys Herbrand’s theorem (Buss Reference Buss1998b; Krajíček Reference Krajíček1995):
$\textrm{PV}_k$
is universal, it enjoys Herbrand’s theorem (Buss Reference Buss1998b; Krajíček Reference Krajíček1995):
Theorem.
(Herbrand) Let
![]() $A(\bar{x}, y)$
and
$A(\bar{x}, y)$
and
![]() $B(\bar{x}, y, z)$
be two quantifier-free
$B(\bar{x}, y, z)$
be two quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formulas. Then:
$\mathcal{L}_{\textrm{PV}_k}$
-formulas. Then:
-
• If
 $\textrm{PV}_k \vdash \exists y A(\bar{x}, y)$
, then there exists an
$\textrm{PV}_k \vdash \exists y A(\bar{x}, y)$
, then there exists an
 $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
 $f(\bar{x})$
such that
$f(\bar{x})$
such that
 $\textrm{PV}_k \vdash A(\bar{x}, f(\bar{x}))$
.
$\textrm{PV}_k \vdash A(\bar{x}, f(\bar{x}))$
. -
• If
 $\textrm{PV}_k \vdash \exists y \forall z B(\bar{x}, y, z)$
, then there are
$\textrm{PV}_k \vdash \exists y \forall z B(\bar{x}, y, z)$
, then there are
 $\mathcal{L}_{\textrm{PV}_k}$
-terms
$\mathcal{L}_{\textrm{PV}_k}$
-terms
 $f_0(\bar{x}), f_1(\bar{x}, z_0), f_2(\bar{x}, z_0, z_1), \ldots,$
$f_0(\bar{x}), f_1(\bar{x}, z_0), f_2(\bar{x}, z_0, z_1), \ldots,$
 $f_m(\bar{x}, z_0, z_1, \ldots, z_{m-1})$
such that
$f_m(\bar{x}, z_0, z_1, \ldots, z_{m-1})$
such that
 $ \bigvee _{i=0}^m B(\bar{x}, f_i(\bar{x}, z_0, \ldots, z_{i-1}), z_{i})$
is provable in
$ \bigvee _{i=0}^m B(\bar{x}, f_i(\bar{x}, z_0, \ldots, z_{i-1}), z_{i})$
is provable in
 $\textrm{PV}_k$
.
$\textrm{PV}_k$
.
It is possible to generalize this theorem to a generalized Herbrand’s theorem to cover more alternations of quantifiers. However, in this paper, one can restrict oneself only to these two levels (Buss Reference Buss1998b).
The system
![]() $\textrm{PV}_k$
proves the scheme
$\textrm{PV}_k$
proves the scheme
![]() $\textrm{PInd}$
for any quantifier-free
$\textrm{PInd}$
for any quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula. As any
$\mathcal{L}_{\textrm{PV}_k}$
-formula. As any
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term can be defined by an
$\mathcal{L}_{\textrm{PV}_k}$
-term can be defined by an
![]() $\mathcal{L}_{\textrm{PV}}$
-formula in
$\mathcal{L}_{\textrm{PV}}$
-formula in
![]() $\hat{\Sigma }^b_k$
, it is possible to represent any quantifier-free
$\hat{\Sigma }^b_k$
, it is possible to represent any quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula by two
$\mathcal{L}_{\textrm{PV}_k}$
-formula by two
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas, one in
$\mathcal{L}_{\textrm{PV}}$
-formulas, one in
![]() $\hat{\Sigma }^b_k$
and one in
$\hat{\Sigma }^b_k$
and one in
![]() $\hat{\Pi }^b_k$
. Using this fact, one can interpret
$\hat{\Pi }^b_k$
. Using this fact, one can interpret
![]() $\textrm{PV}_k$
inside the theory
$\textrm{PV}_k$
inside the theory
![]() $S^k_2$
.
$S^k_2$
.
Going beyond bounded theories of arithmetic, in a similar fashion to
![]() $\textrm{PV}$
and using the construction of primitive recursive functions by composition and primitive recursion on certain basic functions, it is possible to extend the language
$\textrm{PV}$
and using the construction of primitive recursive functions by composition and primitive recursion on certain basic functions, it is possible to extend the language
![]() $\mathcal{L}_{\textrm{PV}}$
by a fresh function symbol for any primitive recursive function. Denote this new language by
$\mathcal{L}_{\textrm{PV}}$
by a fresh function symbol for any primitive recursive function. Denote this new language by
![]() $\mathcal{L}_{\textrm{PRA}}$
and set the first-order theory
$\mathcal{L}_{\textrm{PRA}}$
and set the first-order theory
![]() $\textrm{PRA}$
over
$\textrm{PRA}$
over
![]() $\mathcal{L}_{\textrm{PRA}}$
as
$\mathcal{L}_{\textrm{PRA}}$
as
![]() $\textrm{PV}$
extended by the defining axioms for the new functional symbols and the induction axiom
$\textrm{PV}$
extended by the defining axioms for the new functional symbols and the induction axiom
![]() $A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any quantifier-free formula in the new language. This is of course different from the usual definition of
$A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any quantifier-free formula in the new language. This is of course different from the usual definition of
![]() $\textrm{PRA}$
as its language is extended by the ptime function symbols in
$\textrm{PRA}$
as its language is extended by the ptime function symbols in
![]() $\mathcal{L}_{\textrm{PV}}$
, and the theory itself is extended by the theory
$\mathcal{L}_{\textrm{PV}}$
, and the theory itself is extended by the theory
![]() $\textrm{PV}$
. Moreover, the formula in the induction axiom of
$\textrm{PV}$
. Moreover, the formula in the induction axiom of
![]() $\textrm{PRA}$
may contain the symbols from
$\textrm{PRA}$
may contain the symbols from
![]() $\mathcal{L}_{\textrm{PV}}$
. However, as the functions in the Cobham calculus are constructible as primitive recursive functions, it is clear that the separation of the primitive recursive function symbols and ptime function symbols is just a technical point and is totally immaterial. In fact, our presentation of
$\mathcal{L}_{\textrm{PV}}$
. However, as the functions in the Cobham calculus are constructible as primitive recursive functions, it is clear that the separation of the primitive recursive function symbols and ptime function symbols is just a technical point and is totally immaterial. In fact, our presentation of
![]() $\textrm{PRA}$
is a conservative extension of the usual
$\textrm{PRA}$
is a conservative extension of the usual
![]() $\textrm{PRA}$
and hence has nothing essentially different from the usual
$\textrm{PRA}$
and hence has nothing essentially different from the usual
![]() $\textrm{PRA}$
.
$\textrm{PRA}$
.
By Peano arithmetic, denoted by
![]() $\textrm{PA}$
, we mean the theory
$\textrm{PA}$
, we mean the theory
![]() $\textrm{PV}$
extended by full induction axiom scheme
$\textrm{PV}$
extended by full induction axiom scheme
![]() $A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any formula
$A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any formula
![]() $A(x)$
. This is also different from the usual definition of
$A(x)$
. This is also different from the usual definition of
![]() $\textrm{PA}$
. However, as all of the function symbols in
$\textrm{PA}$
. However, as all of the function symbols in
![]() $\mathcal{L}_{\textrm{PV}}$
are definable in the usual language of
$\mathcal{L}_{\textrm{PV}}$
are definable in the usual language of
![]() $\textrm{PA}$
and their functionality and totality are provable in the usual
$\textrm{PA}$
and their functionality and totality are provable in the usual
![]() $\textrm{PA}$
, it is easy to see that our
$\textrm{PA}$
, it is easy to see that our
![]() $\textrm{PA}$
is a conservative extension of the usual
$\textrm{PA}$
is a conservative extension of the usual
![]() $\textrm{PA}$
.
$\textrm{PA}$
.
By
![]() $\Pi ^0_2$
, we mean the class of
$\Pi ^0_2$
, we mean the class of
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas in the form
$\mathcal{L}_{\textrm{PV}}$
-formulas in the form
![]() $\forall \bar{x} \exists \bar{y}A(\bar{x}, \bar{y})$
, where any quantifier in
$\forall \bar{x} \exists \bar{y}A(\bar{x}, \bar{y})$
, where any quantifier in
![]() $A(\bar{x}, \bar{y})$
is bounded. For two theories
$A(\bar{x}, \bar{y})$
is bounded. For two theories
![]() $T$
and
$T$
and
![]() $S$
and a class of formulas
$S$
and a class of formulas
![]() $\Phi$
, by
$\Phi$
, by
![]() $T \equiv _{\Phi } S$
, we mean
$T \equiv _{\Phi } S$
, we mean
![]() $T \vdash A$
iff
$T \vdash A$
iff
![]() $S \vdash A$
, for any
$S \vdash A$
, for any
![]() $A \in \Phi$
.
$A \in \Phi$
.
Finally, let us recall some basics of the ordinal arithmetic. Apart from addition, multiplication, and exponentiation of the ordinals, it is also possible to define subtraction
![]() $\dot{-}$
from left such that
$\dot{-}$
from left such that
![]() $\alpha \dot{-} \beta =0$
, if
$\alpha \dot{-} \beta =0$
, if
![]() $\alpha \prec \beta$
and
$\alpha \prec \beta$
and
![]() $\alpha \dot{-} \beta =\gamma$
, if
$\alpha \dot{-} \beta =\gamma$
, if
![]() $\beta \preceq \alpha$
, where
$\beta \preceq \alpha$
, where
![]() $\gamma$
is the unique ordinal with the property that
$\gamma$
is the unique ordinal with the property that
![]() $\beta + \gamma =\alpha$
. Similarly, it is possible to define the division
$\beta + \gamma =\alpha$
. Similarly, it is possible to define the division
![]() $d$
from left such that if
$d$
from left such that if
![]() $\beta \neq 0$
, then
$\beta \neq 0$
, then
![]() $d(\alpha, \beta )$
is the unique
$d(\alpha, \beta )$
is the unique
![]() $\gamma$
such that
$\gamma$
such that
![]() $\alpha =\beta \gamma + \delta$
, for some
$\alpha =\beta \gamma + \delta$
, for some
![]() $\delta \prec \beta$
.
$\delta \prec \beta$
.
3. Polynomial-Time Ordinal Representations
In this section, we will introduce polynomial time ordinal representations and recall the concrete representation for the ordinal
![]() $\varepsilon _0$
provided in Beckmann et al. (Reference Beckmann, Pollett and Buss2003). Both parts will be of essential use in Section 4.
$\varepsilon _0$
provided in Beckmann et al. (Reference Beckmann, Pollett and Buss2003). Both parts will be of essential use in Section 4.
Definition 1.
Let
![]() $\alpha$
be an infinite ordinal closed under addition, multiplication, and the operation
$\alpha$
be an infinite ordinal closed under addition, multiplication, and the operation
![]() $\beta \mapsto \omega ^{\beta }$
. We call the tuple
$\beta \mapsto \omega ^{\beta }$
. We call the tuple
a polynomial time representation with a primitive recursive exponentiation (ptime representation, for short) for the ordinal
![]() $\alpha$
, if:
$\alpha$
, if:
-
•
 $\mathcal{O}$
is a unary polynomial time relation on the natural numbers represented as a quantifier-free
$\mathcal{O}$
is a unary polynomial time relation on the natural numbers represented as a quantifier-free
 $\mathcal{L}_{\textrm{PV}}$
-formula. Its intended meaning is the set of all the representations of the ordinals below
$\mathcal{L}_{\textrm{PV}}$
-formula. Its intended meaning is the set of all the representations of the ordinals below
 $\alpha$
. We use small Greek letters to denote the elements of
$\alpha$
. We use small Greek letters to denote the elements of
 $\mathcal{O}$
. For instance, by
$\mathcal{O}$
. For instance, by
 $\forall \beta \, A(\beta )$
, we actually mean
$\forall \beta \, A(\beta )$
, we actually mean
 $\forall x (\mathcal{O}(x) \to A(x))$
.
$\forall x (\mathcal{O}(x) \to A(x))$
. -
•
 $\prec$
is a binary polynomial time relation on the natural numbers, represented as a quantifier-free
$\prec$
is a binary polynomial time relation on the natural numbers, represented as a quantifier-free
 $\mathcal{L}_{\textrm{PV}}$
-formula. Its intended meaning is the order over the ordinals below
$\mathcal{L}_{\textrm{PV}}$
-formula. Its intended meaning is the order over the ordinals below
 $\alpha$
. We define the relation
$\alpha$
. We define the relation
 $(\gamma \preceq \beta )$
as
$(\gamma \preceq \beta )$
as
 $(\gamma \prec \beta ) \vee (\gamma =\beta )$
.
$(\gamma \prec \beta ) \vee (\gamma =\beta )$
. -
•
 $+, \cdot, \dot{-}$
and
$+, \cdot, \dot{-}$
and
 $ d(\cdot, \cdot )$
are binary polynomial time functions, represented as
$ d(\cdot, \cdot )$
are binary polynomial time functions, represented as
 $\mathcal{L}_{\textrm{PV}}$
-terms. Their intended meaning is the ordinal addition, multiplication, subtraction from left, and division from left, respectively.
$\mathcal{L}_{\textrm{PV}}$
-terms. Their intended meaning is the ordinal addition, multiplication, subtraction from left, and division from left, respectively.
-
•
 $o$
is a unary polynomial time function represented as an
$o$
is a unary polynomial time function represented as an
 $\mathcal{L}_{\textrm{PV}}$
-term. Its intended meaning is the function that maps the natural numbers to the representation of their order-types below
$\mathcal{L}_{\textrm{PV}}$
-term. Its intended meaning is the function that maps the natural numbers to the representation of their order-types below
 $\alpha$
. For instance,
$\alpha$
. For instance,
 $o(0)$
is the least element of
$o(0)$
is the least element of
 $\mathcal{O}$
while
$\mathcal{O}$
while
 $o(1)$
is its second least element.
$o(1)$
is its second least element.
-
•
 $\omega ^{x}$
is a primitive recursive unary function represented as an
$\omega ^{x}$
is a primitive recursive unary function represented as an
 $\mathcal{L}_{\textrm{PRA}}$
-term. Its intended meaning is the function that maps the ordinal
$\mathcal{L}_{\textrm{PRA}}$
-term. Its intended meaning is the function that maps the ordinal
 $\beta \prec \alpha$
to the ordinal
$\beta \prec \alpha$
to the ordinal
 $\omega ^{\beta } \prec \alpha$
.
$\omega ^{\beta } \prec \alpha$
. -
•
 $\textbf{0}$
,
$\textbf{0}$
,
 $\textbf{1}$
and
$\textbf{1}$
and
 $\omega$
are three numbers representing the ordinals zero, one and
$\omega$
are three numbers representing the ordinals zero, one and
 $\omega$
, respectively.
$\omega$
, respectively.
-
• The structure
 $(\mathfrak{O}, \prec )$
is isomorphic to
$(\mathfrak{O}, \prec )$
is isomorphic to
 $(\alpha, \prec _{\alpha })$
, where
$(\alpha, \prec _{\alpha })$
, where
 $\prec _{\alpha }$
is the order on
$\prec _{\alpha }$
is the order on
 $\alpha$
.
$\alpha$
. -
•
 $\textrm{PV}$
proves that
$\textrm{PV}$
proves that
 $\prec$
is a total ordering on
$\prec$
is a total ordering on
 $\mathcal{O}$
with the minimum
$\mathcal{O}$
with the minimum
 $\textbf{0}$
.
$\textbf{0}$
. -
•
 $\textrm{PV}$
proves that
$\textrm{PV}$
proves that
 $\prec$
is discrete over
$\prec$
is discrete over
 $\mathcal{O}$
, that is, for all
$\mathcal{O}$
, that is, for all
 $\beta, \gamma \in \mathcal{O}$
, if
$\beta, \gamma \in \mathcal{O}$
, if
 $\gamma \prec \beta +\textbf{1}$
, then either
$\gamma \prec \beta +\textbf{1}$
, then either
 $\gamma \prec \beta$
or
$\gamma \prec \beta$
or
 $ \gamma =\beta$
.
$ \gamma =\beta$
. -
•
 $\textrm{PV}$
proves the associativity of the addition and multiplication, the left distributivity of multiplication over the addition, the neutrality of
$\textrm{PV}$
proves the associativity of the addition and multiplication, the left distributivity of multiplication over the addition, the neutrality of
 $\textbf{0}$
for the addition, the neutrality of
$\textbf{0}$
for the addition, the neutrality of
 $\textbf{1}$
for the multiplication and the identity
$\textbf{1}$
for the multiplication and the identity
 $\textbf{0}\beta =\beta \textbf{0}=\textbf{0}$
.
$\textbf{0}\beta =\beta \textbf{0}=\textbf{0}$
. -
•
 $\textrm{PV}$
proves that the addition and the nonzero multiplication from left respect the order
$\textrm{PV}$
proves that the addition and the nonzero multiplication from left respect the order
 $\prec$
, that is, if
$\prec$
, that is, if
 $\delta \prec \gamma$
then
$\delta \prec \gamma$
then
 $\beta + \delta \prec \beta + \gamma$
and if we also have
$\beta + \delta \prec \beta + \gamma$
and if we also have
 $\beta \neq \textbf{0}$
, then
$\beta \neq \textbf{0}$
, then
 $\beta \delta \prec \beta \gamma$
.
$\beta \delta \prec \beta \gamma$
. -
•
 $\textrm{PV}$
proves that the addition and multiplication from right respects
$\textrm{PV}$
proves that the addition and multiplication from right respects
 $\preceq$
, that is, if
$\preceq$
, that is, if
 $\delta \preceq \gamma$
then
$\delta \preceq \gamma$
then
 $\delta +\beta \preceq \gamma + \beta$
and
$\delta +\beta \preceq \gamma + \beta$
and
 $\delta \beta \preceq \gamma \beta$
.
$\delta \beta \preceq \gamma \beta$
. -
•
 $\textrm{PV}$
proves the defining axioms of
$\textrm{PV}$
proves the defining axioms of
 $\dot{-}$
, that is, if
$\dot{-}$
, that is, if
 $\alpha \prec \beta$
then
$\alpha \prec \beta$
then
 $\alpha \dot{-} \beta =\textbf{0}$
and if
$\alpha \dot{-} \beta =\textbf{0}$
and if
 $\alpha \succeq \beta$
then
$\alpha \succeq \beta$
then
 $\alpha =\beta +(\alpha \dot{-} \beta )$
.
$\alpha =\beta +(\alpha \dot{-} \beta )$
. -
•
 $\textrm{PV}$
proves the defining axioms of
$\textrm{PV}$
proves the defining axioms of
 $d$
, that is, if
$d$
, that is, if
 $\beta \neq \textbf{0}$
, then
$\beta \neq \textbf{0}$
, then
 $\beta d(\alpha, \beta ) \preceq \alpha$
and
$\beta d(\alpha, \beta ) \preceq \alpha$
and
 $\alpha \dot{-} \beta d(\alpha, \beta ) \prec \beta$
.
$\alpha \dot{-} \beta d(\alpha, \beta ) \prec \beta$
. -
•
 $\textrm{PV}$
proves that
$\textrm{PV}$
proves that
 $o$
is an order-isomorphism between the natural numbers and the ordinals below
$o$
is an order-isomorphism between the natural numbers and the ordinals below
 $\omega$
, mapping
$\omega$
, mapping
 $0$
and
$0$
and
 $1$
to
$1$
to
 $\textbf{0}$
and
$\textbf{0}$
and
 $\textbf{1}$
, respectively, that is,
$\textbf{1}$
, respectively, that is,
 $\textrm{PV}$
proves
$\textrm{PV}$
proves
 $o(0)=\textbf{0}$
,
$o(0)=\textbf{0}$
,
 $o(1)=\textbf{1}$
,
$o(1)=\textbf{1}$
,
 $\forall x [\mathcal{O}(o(x)) \wedge o(x) \prec \omega ]$
,
$\forall x [\mathcal{O}(o(x)) \wedge o(x) \prec \omega ]$
,
 $\forall \beta \prec \omega \exists ! y \, o(y)=\beta$
, and
$\forall \beta \prec \omega \exists ! y \, o(y)=\beta$
, and
 $\forall xy (x \lt y \leftrightarrow o(x) \prec o(y))$
. Where there is no risk of confusion, we will use the numbers and their ordinal reinterpretations, interchangeably. For instance, we use
$\forall xy (x \lt y \leftrightarrow o(x) \prec o(y))$
. Where there is no risk of confusion, we will use the numbers and their ordinal reinterpretations, interchangeably. For instance, we use
 $1$
for
$1$
for
 $\textbf{1}$
.
$\textbf{1}$
. -
•
 $\textrm{PRA}$
proves that
$\textrm{PRA}$
proves that
 $\omega ^{\textbf{0}}=1$
and
$\omega ^{\textbf{0}}=1$
and
 $\omega ^{\textbf{1}}=\omega$
. It also proves that
$\omega ^{\textbf{1}}=\omega$
. It also proves that
 $\omega ^{\beta }$
respects
$\omega ^{\beta }$
respects
 $\preceq$
and maps the addition to the multiplication.
$\preceq$
and maps the addition to the multiplication.
-
• If there is no
 $\gamma \in \mathcal{O}$
such that
$\gamma \in \mathcal{O}$
such that
 $\beta =\gamma +1$
, then
$\beta =\gamma +1$
, then
 $\omega ^{\beta }$
is the supremum of the set
$\omega ^{\beta }$
is the supremum of the set
 $\{\omega ^{\gamma } \mid \gamma \prec \beta \}$
, that is, for any
$\{\omega ^{\gamma } \mid \gamma \prec \beta \}$
, that is, for any
 $\delta \in \mathcal{O}$
, if
$\delta \in \mathcal{O}$
, if
 $\omega ^{\gamma } \preceq \delta$
, for any
$\omega ^{\gamma } \preceq \delta$
, for any
 $\gamma \prec \beta$
, then
$\gamma \prec \beta$
, then
 $\omega ^{\beta } \preceq \delta$
.
$\omega ^{\beta } \preceq \delta$
. -
•
 $\textrm{PRA}$
proves that for every
$\textrm{PRA}$
proves that for every
 $\beta \in \mathcal{O}$
, there is a unique expansion
$\beta \in \mathcal{O}$
, there is a unique expansion
 $\beta =\omega ^{\gamma _1}+ \ldots + \omega ^{\gamma _n}$
such that
$\beta =\omega ^{\gamma _1}+ \ldots + \omega ^{\gamma _n}$
such that
 $\gamma _n \preceq \gamma _{n-1} \preceq \ldots \preceq \gamma _1$
.
$\gamma _n \preceq \gamma _{n-1} \preceq \ldots \preceq \gamma _1$
.
Remark 2. Here are some remarks. First, notice that the relations of being a successor and a limit ordinal are both definable by the predicates
![]() $\exists \gamma (\beta =\gamma +1)$
and
$\exists \gamma (\beta =\gamma +1)$
and
![]() $\forall \gamma \prec \beta (\gamma +1 \prec \beta )$
, respectively. It is also easy to see that
$\forall \gamma \prec \beta (\gamma +1 \prec \beta )$
, respectively. It is also easy to see that
![]() $\textrm{PV}$
can prove the dichotomy that for any
$\textrm{PV}$
can prove the dichotomy that for any
![]() $\beta \in \mathcal{O}$
, it is either a successor or a limit. Second, using the compatibility of the order with the addition and the multiplication, one can easily prove in
$\beta \in \mathcal{O}$
, it is either a successor or a limit. Second, using the compatibility of the order with the addition and the multiplication, one can easily prove in
![]() $\textrm{PV}$
that if
$\textrm{PV}$
that if
![]() $\beta =\gamma +\delta =\gamma +\eta$
, then
$\beta =\gamma +\delta =\gamma +\eta$
, then
![]() $\beta \dot{-} \gamma =\delta =\eta$
. This observation proves that for any
$\beta \dot{-} \gamma =\delta =\eta$
. This observation proves that for any
![]() $\gamma \prec \beta$
, the interval
$\gamma \prec \beta$
, the interval
![]() $(\textbf{0}, \beta \dot{-} \gamma )$
in
$(\textbf{0}, \beta \dot{-} \gamma )$
in
![]() $\mathcal{O}$
is in one-to-one correspondence with the interval
$\mathcal{O}$
is in one-to-one correspondence with the interval
![]() $(\gamma, \beta )$
, via the map
$(\gamma, \beta )$
, via the map
![]() $\delta \mapsto \gamma +\delta$
. Similarly,
$\delta \mapsto \gamma +\delta$
. Similarly,
![]() $\textrm{PV}$
proves that if
$\textrm{PV}$
proves that if
![]() $\gamma \neq \textbf{0}$
, then
$\gamma \neq \textbf{0}$
, then
![]() $\beta =\gamma \delta =\gamma \eta$
implies
$\beta =\gamma \delta =\gamma \eta$
implies
![]() $d(\beta, \gamma )=\delta =\eta$
. Therefore,
$d(\beta, \gamma )=\delta =\eta$
. Therefore,
![]() $d(\gamma \delta, \gamma )=\delta$
, for
$d(\gamma \delta, \gamma )=\delta$
, for
![]() $\gamma \neq \textbf{0}$
. Third, let us explain the discrepancy between the polynomial time character of the order, addition, multiplication, subtraction, and division and the primitive recursive character of the function
$\gamma \neq \textbf{0}$
. Third, let us explain the discrepancy between the polynomial time character of the order, addition, multiplication, subtraction, and division and the primitive recursive character of the function
![]() $x \mapsto \omega ^{x}$
in our definition. For that purpose, first, pretend that our definition uses the primitive recursive functions and predicates and
$x \mapsto \omega ^{x}$
in our definition. For that purpose, first, pretend that our definition uses the primitive recursive functions and predicates and
![]() $\textrm{PRA}$
everywhere when it actually uses polynomial time functions and predicates and
$\textrm{PRA}$
everywhere when it actually uses polynomial time functions and predicates and
![]() $\textrm{PV}$
. Then, one can easily see that this primitive recursive version of our representation is just a mild extension of the primitive recursive (even elementary) ordinal representation employed in Friedman and Sheard (Reference Friedman and Sheard1995). (Their conditions are different, but it is easy to show that our axioms imply theirs.) As we use a proof-theoretic result of Friedman and Sheard (Reference Friedman and Sheard1995), using the primitive recursive version of our definition is completely justified. However, there is another role for our ordinal representation. As it is clear, in this paper, we intend to address the lower complexity formulas and for that purpose, some basic ordinal arithmetic (up to addition and multiplication and hence subtraction and division from left) is required to be implemented in polynomial time. Therefore, we are forced to lower the complexity of some parts of the representation. However, as the use of the exponentiation is only restricted to the result from Friedman and Sheard (Reference Friedman and Sheard1995) that we use as a black box here, we decided to lower the complexity up to the point we need and let the exponentiation parts intact. This way we can accept more ptime representations.
$\textrm{PV}$
. Then, one can easily see that this primitive recursive version of our representation is just a mild extension of the primitive recursive (even elementary) ordinal representation employed in Friedman and Sheard (Reference Friedman and Sheard1995). (Their conditions are different, but it is easy to show that our axioms imply theirs.) As we use a proof-theoretic result of Friedman and Sheard (Reference Friedman and Sheard1995), using the primitive recursive version of our definition is completely justified. However, there is another role for our ordinal representation. As it is clear, in this paper, we intend to address the lower complexity formulas and for that purpose, some basic ordinal arithmetic (up to addition and multiplication and hence subtraction and division from left) is required to be implemented in polynomial time. Therefore, we are forced to lower the complexity of some parts of the representation. However, as the use of the exponentiation is only restricted to the result from Friedman and Sheard (Reference Friedman and Sheard1995) that we use as a black box here, we decided to lower the complexity up to the point we need and let the exponentiation parts intact. This way we can accept more ptime representations.
Let
![]() $\beta \in \mathcal{O}$
. By the axiom scheme
$\beta \in \mathcal{O}$
. By the axiom scheme
![]() $\textrm{TI}({\prec_{\beta}})$
, we mean the transfinite induction up to
$\textrm{TI}({\prec_{\beta}})$
, we mean the transfinite induction up to
![]() $\beta$
, that is
$\beta$
, that is
where
![]() $A$
can be any formula in
$A$
can be any formula in
![]() $\mathcal{L}_{\textrm{PV}}$
. In Friedman and Sheard (Reference Friedman and Sheard1995), a refined method of ordinal analysis is provided showing that the
$\mathcal{L}_{\textrm{PV}}$
. In Friedman and Sheard (Reference Friedman and Sheard1995), a refined method of ordinal analysis is provided showing that the
![]() $\Pi ^0_2$
-consequences of the theory
$\Pi ^0_2$
-consequences of the theory
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}} \textrm{TI}({\prec_{\beta}})$
are actually provable in a smaller theory extending
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}} \textrm{TI}({\prec_{\beta}})$
are actually provable in a smaller theory extending
![]() $\textrm{PRA}$
with a weak form of transfinite induction stating that for any
$\textrm{PRA}$
with a weak form of transfinite induction stating that for any
![]() $\beta \prec \alpha$
, there is no primitive recursive decreasing sequence of ordinals below
$\beta \prec \alpha$
, there is no primitive recursive decreasing sequence of ordinals below
![]() $\beta$
. For more, see Friedman and Sheard (Reference Friedman and Sheard1995), Rathjen (Reference Rathjen1999).
$\beta$
. For more, see Friedman and Sheard (Reference Friedman and Sheard1995), Rathjen (Reference Rathjen1999).
Theorem.
Let
![]() $\alpha$
be an ordinal and
$\alpha$
be an ordinal and
![]() $\mathfrak{O}$
be its ptime representation. Then,
$\mathfrak{O}$
be its ptime representation. Then,
where
![]() $\textrm{PRWO}({\prec_{\beta}})$
is the scheme
$\textrm{PRWO}({\prec_{\beta}})$
is the scheme
![]() $ \forall \bar{x} \exists y [f(\bar{x}, y+1) \nprec f(\bar{x}, y) \vee \neg \mathcal{O}(f(\bar{x}, y)) \vee f(\bar{x}, y) \nprec \beta ]$
, for any function symbol
$ \forall \bar{x} \exists y [f(\bar{x}, y+1) \nprec f(\bar{x}, y) \vee \neg \mathcal{O}(f(\bar{x}, y)) \vee f(\bar{x}, y) \nprec \beta ]$
, for any function symbol
![]() $f$
in
$f$
in
![]() $\mathcal{L}_{\textrm{PRA}}$
.
$\mathcal{L}_{\textrm{PRA}}$
.
3.1 A polynomial-time representation for
 $\varepsilon _0$
$\varepsilon _0$
In this subsection, we will recall the basics of the ptime notation system for the ordinal
![]() $\varepsilon _0$
, introduced in Beckmann et al. (Reference Beckmann, Pollett and Buss2003). Define
$\varepsilon _0$
, introduced in Beckmann et al. (Reference Beckmann, Pollett and Buss2003). Define
![]() $\mathcal{O}_{0}$
and
$\mathcal{O}_{0}$
and
![]() $\prec _{0}$
inductively and simultaneously in the following way:
$\prec _{0}$
inductively and simultaneously in the following way:
![]() $\mathcal{O}_{0}$
is the least set of expressions containing the empty string
$\mathcal{O}_{0}$
is the least set of expressions containing the empty string
![]() $\textbf{0}$
and is closed under the operation
$\textbf{0}$
and is closed under the operation
![]() $(\alpha _1, \ldots, \alpha _n) \mapsto \omega ^{\alpha _1}a_1+ \ldots +\omega ^{\alpha _n}a_n$
, where
$(\alpha _1, \ldots, \alpha _n) \mapsto \omega ^{\alpha _1}a_1+ \ldots +\omega ^{\alpha _n}a_n$
, where
![]() $a_i \neq 0$
are natural numbers and
$a_i \neq 0$
are natural numbers and
![]() $\alpha _n \prec _{0} \ldots \prec _{0} \alpha _2 \prec _{0} \alpha _1$
and set
$\alpha _n \prec _{0} \ldots \prec _{0} \alpha _2 \prec _{0} \alpha _1$
and set
![]() $\omega ^{\alpha _1}a_1+ \ldots +\omega ^{\alpha _n}a_n \prec _{0} \omega ^{\beta _1}b_1+ \ldots +\omega ^{\beta _m}b_m$
, if there exists
$\omega ^{\alpha _1}a_1+ \ldots +\omega ^{\alpha _n}a_n \prec _{0} \omega ^{\beta _1}b_1+ \ldots +\omega ^{\beta _m}b_m$
, if there exists
![]() $i \leq \min\{m,n\}$
such that
$i \leq \min\{m,n\}$
such that
![]() $\alpha _j=\beta _j$
and
$\alpha _j=\beta _j$
and
![]() $a_j=b_j$
, for any
$a_j=b_j$
, for any
![]() $j \leq i$
and one of the following takes place:
$j \leq i$
and one of the following takes place:
-
•
 $i=n\lt m$
,
$i=n\lt m$
, -
•
 $i \lt \min\{m,n\}$
and
$i \lt \min\{m,n\}$
and
 $\alpha _{i+1} \prec _{0} \beta _{i+1}$
$\alpha _{i+1} \prec _{0} \beta _{i+1}$
-
•
 $i \lt \min\{m,n\}$
and
$i \lt \min\{m,n\}$
and
 $\alpha _{i+1} = \beta _{i+1}$
and
$\alpha _{i+1} = \beta _{i+1}$
and
 $a_i \lt b_i$
.
$a_i \lt b_i$
.
Using some efficient method of sequence encoding, it is possible to arithmetize the set
![]() $\mathcal{O}_{0}$
and the predicate
$\mathcal{O}_{0}$
and the predicate
![]() $\prec _{0}$
. It is also possible to implement the arithmetization in a way that the length of the Gödel number of
$\prec _{0}$
. It is also possible to implement the arithmetization in a way that the length of the Gödel number of
![]() $\alpha \in \mathcal{O}_{0}$
is proportional to the number of symbols in the expression
$\alpha \in \mathcal{O}_{0}$
is proportional to the number of symbols in the expression
![]() $\alpha$
. By this fact, Beckmann et al. (Reference Beckmann, Pollett and Buss2003) shows that both
$\alpha$
. By this fact, Beckmann et al. (Reference Beckmann, Pollett and Buss2003) shows that both
![]() $\mathcal{O}_{0}$
and
$\mathcal{O}_{0}$
and
![]() $\prec _{0}$
are polynomial time computable and hence formalizable in
$\prec _{0}$
are polynomial time computable and hence formalizable in
![]() $\textrm{PV}$
. (Technically, it uses a conservative extension of
$\textrm{PV}$
. (Technically, it uses a conservative extension of
![]() $\textrm{PV}$
, but the difference does not affect us here.) We fix quantifier-free predicates
$\textrm{PV}$
, but the difference does not affect us here.) We fix quantifier-free predicates
![]() $\mathcal{O}_{0}(x)$
and
$\mathcal{O}_{0}(x)$
and
![]() $x \prec _{0} y$
to denote the formalized versions in the language
$x \prec _{0} y$
to denote the formalized versions in the language
![]() $\mathcal{L}_{\textrm{PV}}$
. In Beckmann et al. (Reference Beckmann, Pollett and Buss2003), it is shown that
$\mathcal{L}_{\textrm{PV}}$
. In Beckmann et al. (Reference Beckmann, Pollett and Buss2003), it is shown that
![]() $\textrm{PV}$
proves that
$\textrm{PV}$
proves that
![]() $\prec$
is a total ordering on
$\prec$
is a total ordering on
![]() $\mathcal{O}_{0}$
. It is clear that
$\mathcal{O}_{0}$
. It is clear that
![]() $\textrm{PV}$
also proves that
$\textrm{PV}$
also proves that
![]() $\textbf{0}$
is the minimum element of
$\textbf{0}$
is the minimum element of
![]() $\mathcal{O}_{0}$
. Define
$\mathcal{O}_{0}$
. Define
![]() $\textbf{1}$
as
$\textbf{1}$
as
![]() $\omega ^{\textbf{0}}1$
and for
$\omega ^{\textbf{0}}1$
and for
![]() $o$
, consider the function that maps the number
$o$
, consider the function that maps the number
![]() $n$
to
$n$
to
![]() $\omega ^{\textbf{0}}n$
. Denote
$\omega ^{\textbf{0}}n$
. Denote
![]() $\omega ^{o(1)}$
by
$\omega ^{o(1)}$
by
![]() $\omega$
. Then, we have
$\omega$
. Then, we have
![]() $\omega ^{\textbf{0}}=\textbf{1}$
and
$\omega ^{\textbf{0}}=\textbf{1}$
and
![]() $\omega ^{\textbf{1}}=\omega$
. The map
$\omega ^{\textbf{1}}=\omega$
. The map
![]() $o$
is ptime, and it is easy to prove in
$o$
is ptime, and it is easy to prove in
![]() $\textrm{PV}$
that
$\textrm{PV}$
that
![]() $o$
is an order-isomorphism, that is,
$o$
is an order-isomorphism, that is,
![]() $\textrm{PV} \vdash \forall x [\mathcal{O}_{0}(o(x)) \wedge o(x) \prec \omega ]$
,
$\textrm{PV} \vdash \forall x [\mathcal{O}_{0}(o(x)) \wedge o(x) \prec \omega ]$
,
![]() $\textrm{PV} \vdash \forall \alpha \prec \omega \exists ! y \, o(y)=\alpha$
and
$\textrm{PV} \vdash \forall \alpha \prec \omega \exists ! y \, o(y)=\alpha$
and
![]() $\textrm{PV} \vdash x \lt y \leftrightarrow o(x) \prec _{0} o(y)$
. For
$\textrm{PV} \vdash x \lt y \leftrightarrow o(x) \prec _{0} o(y)$
. For
![]() $x \mapsto \omega ^x$
, use the evident function mapping the expression
$x \mapsto \omega ^x$
, use the evident function mapping the expression
![]() $\beta$
to the expression
$\beta$
to the expression
![]() $\omega ^{\beta }$
and note that it is clearly primitive recursive.
$\omega ^{\beta }$
and note that it is clearly primitive recursive.
In the rest of this subsection, we will explain how to formalize the basic ordinal arithmetic in
![]() $\textrm{PV}$
, using the aforementioned representation. For that purpose, first consider the following equalities over the real ordinals below
$\textrm{PV}$
, using the aforementioned representation. For that purpose, first consider the following equalities over the real ordinals below
![]() $\varepsilon _0$
. We assumed that the inputs are nonzero as the operations with one zero input are trivial. These equalities make the computation of the addition, multiplication, subtraction from left and division from left possible, using the Cantor normal form of the ordinals. We will not provide a proof for these equalities as they are just simple computations, see Takeuti and Zaring (Reference Takeuti and Zaring1982).
$\varepsilon _0$
. We assumed that the inputs are nonzero as the operations with one zero input are trivial. These equalities make the computation of the addition, multiplication, subtraction from left and division from left possible, using the Cantor normal form of the ordinals. We will not provide a proof for these equalities as they are just simple computations, see Takeuti and Zaring (Reference Takeuti and Zaring1982).
 \begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)+\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} \sum _{i=1}^n \omega ^{\alpha _i}a_i+\sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _n \succ \beta _1 \\ \sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _1 \prec \beta _1\\ \sum _{i=1}^{k} \omega ^{\alpha _i}a_i+ \sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _{k+1} \prec \beta _1 \prec \alpha _{k}\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i}a_i+\omega ^{\alpha _k}(a_k+b_1) +\sum _{j=2}^m \omega ^{\beta _j}b_j & \alpha _{k}=\beta _1 \end {cases} } \end{equation*}
\begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)+\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} \sum _{i=1}^n \omega ^{\alpha _i}a_i+\sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _n \succ \beta _1 \\ \sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _1 \prec \beta _1\\ \sum _{i=1}^{k} \omega ^{\alpha _i}a_i+ \sum _{j=1}^m \omega ^{\beta _j}b_j & \alpha _{k+1} \prec \beta _1 \prec \alpha _{k}\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i}a_i+\omega ^{\alpha _k}(a_k+b_1) +\sum _{j=2}^m \omega ^{\beta _j}b_j & \alpha _{k}=\beta _1 \end {cases} } \end{equation*}
 \begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)\dot {-}\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} 0 & \alpha _{k+1} \prec \beta _{k+1} \\ \sum _{i=k+1}^n \omega ^{\alpha _i}a_i & \alpha _{k+1} \succ \beta _{k+1}\\ \omega ^{\alpha _{k+1}}(a_{k+1}-b_{k+1})+\sum _{i=k+2}^n \omega ^{\alpha _i}a_i & \alpha _{k+1} = \beta _{k+1}, a_{k+1}\gt b_{k+1}\\ 0 & \alpha _{k+1} = \beta _{k+1}, a_{k+1}\lt b_{k+1} \end {cases} } \end{equation*}
\begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)\dot {-}\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} 0 & \alpha _{k+1} \prec \beta _{k+1} \\ \sum _{i=k+1}^n \omega ^{\alpha _i}a_i & \alpha _{k+1} \succ \beta _{k+1}\\ \omega ^{\alpha _{k+1}}(a_{k+1}-b_{k+1})+\sum _{i=k+2}^n \omega ^{\alpha _i}a_i & \alpha _{k+1} = \beta _{k+1}, a_{k+1}\gt b_{k+1}\\ 0 & \alpha _{k+1} = \beta _{k+1}, a_{k+1}\lt b_{k+1} \end {cases} } \end{equation*}
where
![]() $k$
is the maximum
$k$
is the maximum
![]() $i$
such that
$i$
such that
![]() $\alpha _i=\beta _i$
and
$\alpha _i=\beta _i$
and
![]() $a_i=b_i$
, if there is any and otherwise
$a_i=b_i$
, if there is any and otherwise
![]() $k=0$
,
$k=0$
,
 \begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} \sum _{j=1}^m \omega ^{\alpha _1+\beta _j}b_j & \beta _m \succ 0 \\ \sum _{j=1}^{m-1} \omega ^{\alpha _1+\beta _j}b_j+\omega ^{\alpha _1}a_1b_m+\sum _{i=2}^n \omega ^{\alpha _i}a_i & \beta _m = 0, m \gt 1\\ \omega ^{\alpha _1}a_1b_1+\sum _{i=2}^n \omega ^{\alpha _i}a_i & \beta _m = 0, m=1 \end {cases} } \end{equation*}
\begin{equation*} { \bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i\bigg)\bigg(\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} \sum _{j=1}^m \omega ^{\alpha _1+\beta _j}b_j & \beta _m \succ 0 \\ \sum _{j=1}^{m-1} \omega ^{\alpha _1+\beta _j}b_j+\omega ^{\alpha _1}a_1b_m+\sum _{i=2}^n \omega ^{\alpha _i}a_i & \beta _m = 0, m \gt 1\\ \omega ^{\alpha _1}a_1b_1+\sum _{i=2}^n \omega ^{\alpha _i}a_i & \beta _m = 0, m=1 \end {cases} } \end{equation*}
 \begin{equation*} { d\bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i,\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} 0 & \alpha _1 \prec \beta _1 \\ \sum _{i=1}^k \omega ^{\alpha _i \dot {-} \beta _1}a_i & \alpha _1 \succeq \beta _1, \alpha _{k} \neq \beta _1\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i \dot {-} \beta _1}a_i+d(a_k,b_1) & \alpha _1 \succeq \beta _1, \alpha _{k} = \beta _1, (*)\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i \dot {-} \beta _1}a_i+(d(a_k,b_1)-1) & \text {otherwise} \end {cases} } \end{equation*}
\begin{equation*} { d\bigg(\sum _{i=1}^n \omega ^{\alpha _i}a_i,\sum _{j=1}^m \omega ^{\beta _j}b_j\bigg)= \begin {cases} 0 & \alpha _1 \prec \beta _1 \\ \sum _{i=1}^k \omega ^{\alpha _i \dot {-} \beta _1}a_i & \alpha _1 \succeq \beta _1, \alpha _{k} \neq \beta _1\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i \dot {-} \beta _1}a_i+d(a_k,b_1) & \alpha _1 \succeq \beta _1, \alpha _{k} = \beta _1, (*)\\ \sum _{i=1}^{k-1} \omega ^{\alpha _i \dot {-} \beta _1}a_i+(d(a_k,b_1)-1) & \text {otherwise} \end {cases} } \end{equation*}
where
![]() $k$
is the greatest
$k$
is the greatest
![]() $i$
such that
$i$
such that
![]() $\alpha _i \succeq \beta _1$
,
$\alpha _i \succeq \beta _1$
,
![]() $d(a_k,b_1)$
is the quotient of
$d(a_k,b_1)$
is the quotient of
![]() $a_k$
divided by
$a_k$
divided by
![]() $b_1$
and
$b_1$
and
![]() $(*)$
is the condition that
$(*)$
is the condition that
![]() $\sum _{i=k}^n \omega ^{\alpha _i}a_i \succeq \omega ^{\alpha _k}b_1d(a_k,b_1)+\sum _{j=2}^m \omega ^{\beta _j}b_j$
. Note that to compute any of the operations, it is enough to do constant many comparisons and basic numerical computations, a search to find the maximum index that takes at most as long as the length of the inputs and at most
$\sum _{i=k}^n \omega ^{\alpha _i}a_i \succeq \omega ^{\alpha _k}b_1d(a_k,b_1)+\sum _{j=2}^m \omega ^{\beta _j}b_j$
. Note that to compute any of the operations, it is enough to do constant many comparisons and basic numerical computations, a search to find the maximum index that takes at most as long as the length of the inputs and at most
![]() $m$
or
$m$
or
![]() $n$
many applications of a ptime function. Hence, all the operations are ptime and hence representable in
$n$
many applications of a ptime function. Hence, all the operations are ptime and hence representable in
![]() $\textrm{PV}$
. It is easy to see but tedious to show that all the claimed properties in Definition 1 hold. Therefore, the described data in this subsection defines a ptime representation for
$\textrm{PV}$
. It is easy to see but tedious to show that all the claimed properties in Definition 1 hold. Therefore, the described data in this subsection defines a ptime representation for
![]() $\varepsilon _0$
that we denote by
$\varepsilon _0$
that we denote by
![]() $\mathfrak{O}_{0}$
.
$\mathfrak{O}_{0}$
.
4. Ordinal Flows and Arithmetic
Let
![]() $\alpha$
be an ordinal and
$\alpha$
be an ordinal and
![]() $\mathfrak{O}$
be its ptime representation. In this section, we develop a witnessing method for the theory
$\mathfrak{O}$
be its ptime representation. In this section, we develop a witnessing method for the theory
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
. The section consists of three parts. First, in Subsection 4.1, we will introduce an auxiliary theory
$\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
. The section consists of three parts. First, in Subsection 4.1, we will introduce an auxiliary theory
![]() $\textrm{TI}(\forall _1, \prec )$
with a transfinite induction on the universal formulas in the language of
$\textrm{TI}(\forall _1, \prec )$
with a transfinite induction on the universal formulas in the language of
![]() $\textrm{PV}$
. The system is powerful enough to interpret
$\textrm{PV}$
. The system is powerful enough to interpret
![]() $\textrm{PRA}+\bigcup _{\beta \in \mathcal{O}} \textrm{PRWO}({\prec_{\beta}})$
and hence proves all
$\textrm{PRA}+\bigcup _{\beta \in \mathcal{O}} \textrm{PRWO}({\prec_{\beta}})$
and hence proves all
![]() $\Pi ^0_2$
-theorems of
$\Pi ^0_2$
-theorems of
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
. Then in Subsection 4.2, we will provide a witnessing method for
$\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
. Then in Subsection 4.2, we will provide a witnessing method for
![]() $\textrm{TI}(\forall _1, \prec )$
that transforms the provability between two universal formulas in
$\textrm{TI}(\forall _1, \prec )$
that transforms the provability between two universal formulas in
![]() $\textrm{TI}(\forall _1, \prec )$
to an ordinal-length sequence of
$\textrm{TI}(\forall _1, \prec )$
to an ordinal-length sequence of
![]() $\textrm{PV}$
-provable implications. Finally, in Subsection 4.3, we use Herbrand’s theorem, Theorem 2, to witness the implications in
$\textrm{PV}$
-provable implications. Finally, in Subsection 4.3, we use Herbrand’s theorem, Theorem 2, to witness the implications in
![]() $\textrm{PV}$
to provide a characterization for the low complexity theorems of
$\textrm{PV}$
to provide a characterization for the low complexity theorems of
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
.
$\textrm{PA}+\bigcup _{\beta \in \mathcal{{O}}}\textrm{TI}({\prec_{\beta}})$
.
4.1 The system
 $\textrm{TI}(\forall _1, \prec )$
$\textrm{TI}(\forall _1, \prec )$
This subsection is devoted to the introduction and investigation of the auxiliary theory
![]() $\textrm{TI}(\forall _1, \prec )$
.
$\textrm{TI}(\forall _1, \prec )$
.
Definition 3.
Define
![]() $\forall _1$
(resp.,
$\forall _1$
(resp.,
![]() $\exists _1$
) as the least set of
$\exists _1$
) as the least set of
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas containing all atomic formulas and their negations and closed under conjunction, disjunction, and universal (resp. existential) quantifiers.
$\mathcal{L}_{\textrm{PV}}$
-formulas containing all atomic formulas and their negations and closed under conjunction, disjunction, and universal (resp. existential) quantifiers.
Let
![]() $I\forall _1$
(resp.
$I\forall _1$
(resp.
![]() $I\exists _1$
) be the theory extending
$I\exists _1$
) be the theory extending
![]() $\textrm{PV}$
by the
$\textrm{PV}$
by the
![]() $\forall _1$
-induction (resp.
$\forall _1$
-induction (resp.
![]() $\exists _1$
-induction) scheme, that is,
$\exists _1$
-induction) scheme, that is,
![]() $A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any
$A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
, for any
![]() $A(x) \in \forall _1$
(resp.
$A(x) \in \forall _1$
(resp.
![]() $A(x) \in \exists _1$
). Note that
$A(x) \in \exists _1$
). Note that
![]() $I\exists _1=I\forall _1$
. The proof uses the usual technique of using
$I\exists _1=I\forall _1$
. The proof uses the usual technique of using
![]() $\forall _1$
-induction on
$\forall _1$
-induction on
![]() $B(x)=\neg A(y \dot{-} x)$
to prove
$B(x)=\neg A(y \dot{-} x)$
to prove
![]() $\exists _1$
-induction on
$\exists _1$
-induction on
![]() $A(y)$
and similarly for the other direction, see Buss (Reference Buss1998).
$A(y)$
and similarly for the other direction, see Buss (Reference Buss1998).
Lemma 4.
For any primitive recursive function
![]() $f: \mathbb{N}^k \to \mathbb{N}$
, there is a
$f: \mathbb{N}^k \to \mathbb{N}$
, there is a
![]() $\exists _1$
-formula
$\exists _1$
-formula
![]() $D_f(\bar{x}, y)$
such that
$D_f(\bar{x}, y)$
such that
![]() $I\exists _1 \vdash \forall \bar{x} \exists ! y D_f(\bar{x}, y)$
and
$I\exists _1 \vdash \forall \bar{x} \exists ! y D_f(\bar{x}, y)$
and
![]() $\mathbb{N} \vDash D_f(\bar{n},m)$
iff
$\mathbb{N} \vDash D_f(\bar{n},m)$
iff
![]() $f(\bar{n})=m$
, for any
$f(\bar{n})=m$
, for any
![]() $\bar{n}, m \in \mathbb{N}$
.
$\bar{n}, m \in \mathbb{N}$
.
Proof.
For any primitive recursive function
![]() $f$
, we provide a quantifier-free formula
$f$
, we provide a quantifier-free formula
![]() $C_f(\bar{x}, w, y) \in \mathcal{L}_{\textrm{PV}}$
encoding that
$C_f(\bar{x}, w, y) \in \mathcal{L}_{\textrm{PV}}$
encoding that
![]() $w$
is a computation of
$w$
is a computation of
![]() $f$
with the input
$f$
with the input
![]() $\bar{x}$
and the output
$\bar{x}$
and the output
![]() $y$
. To that aim, we use recursion on the construction of
$y$
. To that aim, we use recursion on the construction of
![]() $f$
. The cases for the basic functions and composition are easy. For the recursion case, if
$f$
. The cases for the basic functions and composition are easy. For the recursion case, if
![]() $f(\bar{x}, y)$
is defined via recursive equations
$f(\bar{x}, y)$
is defined via recursive equations
![]() $f(\bar{x}, 0)=g(\bar{x})$
and
$f(\bar{x}, 0)=g(\bar{x})$
and
![]() $f(\bar{x}, y+1)=h(\bar{x}, y, f(\bar{x}, y))$
, define
$f(\bar{x}, y+1)=h(\bar{x}, y, f(\bar{x}, y))$
, define
![]() $C_f(\bar{x}, y, \langle u, v \rangle, z)$
as
$C_f(\bar{x}, y, \langle u, v \rangle, z)$
as
![]() $C_g(\bar{x}, u_0, v_0) \wedge \forall i \leq l(v) C_h(\bar{x}, i, v_i, u_{i+1}, v_{i+1}) \wedge v_{l(v)}=z$
, where
$C_g(\bar{x}, u_0, v_0) \wedge \forall i \leq l(v) C_h(\bar{x}, i, v_i, u_{i+1}, v_{i+1}) \wedge v_{l(v)}=z$
, where
![]() $v$
encodes the sequence
$v$
encodes the sequence
![]() $\{f(\bar{x}, i)\}_{i=0}^{l(v)}$
, the number
$\{f(\bar{x}, i)\}_{i=0}^{l(v)}$
, the number
![]() $l(v)$
is the length of this sequence and
$l(v)$
is the length of this sequence and
![]() $u$
encodes the sequence of computations
$u$
encodes the sequence of computations
![]() $\{u_{i}\}_{i=0}^{l(v)}$
, where
$\{u_{i}\}_{i=0}^{l(v)}$
, where
![]() $u_0$
reads
$u_0$
reads
![]() $\bar{x}$
and computes
$\bar{x}$
and computes
![]() $v_0=f(\bar{x}, 0)$
and
$v_0=f(\bar{x}, 0)$
and
![]() $u_{i+1}$
reads
$u_{i+1}$
reads
![]() $\bar{x}$
,
$\bar{x}$
,
![]() $i$
and
$i$
and
![]() $f(\bar{x}, i)$
and computes
$f(\bar{x}, i)$
and computes
![]() $f(\bar{x}, i+1)$
via the function
$f(\bar{x}, i+1)$
via the function
![]() $h$
. Note that the predicate
$h$
. Note that the predicate
![]() $\forall i \leq l(v) C_h(\bar{x}, i, v_i, u_i, v_{i+1})$
is polynomial computable, as
$\forall i \leq l(v) C_h(\bar{x}, i, v_i, u_i, v_{i+1})$
is polynomial computable, as
![]() $l(v) \leq |v|$
, where
$l(v) \leq |v|$
, where
![]() $|v|$
is the binary length of
$|v|$
is the binary length of
![]() $v$
. Hence, there exists a polynomial time function symbol in
$v$
. Hence, there exists a polynomial time function symbol in
![]() $\textrm{PV}$
like
$\textrm{PV}$
like
![]() $F$
such that
$F$
such that
![]() $\textrm{PV}$
proves that
$\textrm{PV}$
proves that
![]() $F(\bar{x}, u, v)=1$
iff
$F(\bar{x}, u, v)=1$
iff
![]() $\forall i \leq l(v) C_h(\bar{x}, i, v_i, u_i, v_{i+1})$
. Therefore,
$\forall i \leq l(v) C_h(\bar{x}, i, v_i, u_i, v_{i+1})$
. Therefore,
![]() $C_f$
can be written in a quantifier-free form. Now, set
$C_f$
can be written in a quantifier-free form. Now, set
![]() $D_f(\bar{x}, y)=\exists w C_f(\bar{x}, w, y)$
. It is clear that
$D_f(\bar{x}, y)=\exists w C_f(\bar{x}, w, y)$
. It is clear that
![]() $D_f \in \exists _1$
and
$D_f \in \exists _1$
and
![]() $\mathbb{N} \vDash D_f(\bar{n},m)$
iff
$\mathbb{N} \vDash D_f(\bar{n},m)$
iff
![]() $f(\bar{n})=m$
, for any
$f(\bar{n})=m$
, for any
![]() $\bar{n}, m \in \mathbb{N}$
. Finally, the proof of the claim that
$\bar{n}, m \in \mathbb{N}$
. Finally, the proof of the claim that
![]() $I\exists _1 \vdash \forall \bar{x} \exists ! y D_f(\bar{x},y)$
is similar to the similar claim in the representation of primitive recursive functions in
$I\exists _1 \vdash \forall \bar{x} \exists ! y D_f(\bar{x},y)$
is similar to the similar claim in the representation of primitive recursive functions in
![]() $I\Sigma _1$
.
$I\Sigma _1$
.
Definition 5.
Define the theory
![]() $\textrm{TI}(\forall _1, \prec )$
over
$\textrm{TI}(\forall _1, \prec )$
over
![]() $\mathcal{L}_{\textrm{PV}}$
as the theory
$\mathcal{L}_{\textrm{PV}}$
as the theory
![]() $\textrm{PV}$
extended by the transfinite induction scheme
$\textrm{PV}$
extended by the transfinite induction scheme
![]() $\forall \delta (\forall \gamma \prec \delta \; A(\gamma ) \to A(\delta )) \to A(\theta )$
, for any
$\forall \delta (\forall \gamma \prec \delta \; A(\gamma ) \to A(\delta )) \to A(\theta )$
, for any
![]() $A(\gamma ) \in \forall _1$
and any constant
$A(\gamma ) \in \forall _1$
and any constant
![]() $\theta \in \mathcal{O}$
.
$\theta \in \mathcal{O}$
.
Note that
![]() $\textrm{TI}(\forall _1, \prec )$
extends the theory
$\textrm{TI}(\forall _1, \prec )$
extends the theory
![]() $I\forall _1$
as
$I\forall _1$
as
![]() $\textrm{TI}(\forall _1, \prec )$
proves
$\textrm{TI}(\forall _1, \prec )$
proves
![]() $\forall \delta \prec \omega (\forall \gamma \prec \delta \; A(\gamma ) \to A(\delta )) \to \forall \delta \prec \omega A(\delta )$
, for any
$\forall \delta \prec \omega (\forall \gamma \prec \delta \; A(\gamma ) \to A(\delta )) \to \forall \delta \prec \omega A(\delta )$
, for any
![]() $A \in \forall _1$
. Using the function
$A \in \forall _1$
. Using the function
![]() $o$
and the fact that it is an order-isomorphism between the numbers and the ordinals below
$o$
and the fact that it is an order-isomorphism between the numbers and the ordinals below
![]() $\omega$
, we will have
$\omega$
, we will have
![]() $\forall x (\forall y \lt x \; A(y) \to A(x)) \to \forall x A(x)$
which implies
$\forall x (\forall y \lt x \; A(y) \to A(x)) \to \forall x A(x)$
which implies
![]() $A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
. Therefore, by Lemma 4,
$A(0) \wedge \forall x (A(x) \to A(x+1)) \to \forall x A(x)$
. Therefore, by Lemma 4,
![]() $\textrm{TI}(\forall _1, \prec )$
represents any primitive recursive function with an
$\textrm{TI}(\forall _1, \prec )$
represents any primitive recursive function with an
![]() $\exists _1$
-definition. As it is routine in arithmetic (Buss Reference Buss1998), this provides both
$\exists _1$
-definition. As it is routine in arithmetic (Buss Reference Buss1998), this provides both
![]() $\forall _1$
and
$\forall _1$
and
![]() $\exists _1$
definitions for any atomic formula in
$\exists _1$
definitions for any atomic formula in
![]() $\mathcal{L}_{\textrm{PRA}}$
. Hence, it is possible to interpret any
$\mathcal{L}_{\textrm{PRA}}$
. Hence, it is possible to interpret any
![]() $\forall _1$
-formula in
$\forall _1$
-formula in
![]() $\mathcal{L}_{\textrm{PRA}}$
as an
$\mathcal{L}_{\textrm{PRA}}$
as an
![]() $\forall _1$
-formula in
$\forall _1$
-formula in
![]() $\mathcal{L}_{\textrm{PV}}$
. Using that interpretation, we can pretend that
$\mathcal{L}_{\textrm{PV}}$
. Using that interpretation, we can pretend that
![]() $\textrm{TI}(\forall _1, \prec )$
has a fresh function symbol for any primitive recursive function and the
$\textrm{TI}(\forall _1, \prec )$
has a fresh function symbol for any primitive recursive function and the
![]() $\forall _1$
-formulas in the new language are allowed in the transfinite induction. Moreover, we can also pretend that
$\forall _1$
-formulas in the new language are allowed in the transfinite induction. Moreover, we can also pretend that
![]() $\textrm{TI}(\forall _1, \prec )$
extends the theory
$\textrm{TI}(\forall _1, \prec )$
extends the theory
![]() $\textrm{PRA}$
. The reason simply is that the equational defining axioms in
$\textrm{PRA}$
. The reason simply is that the equational defining axioms in
![]() $\textrm{PRA}$
are all provable in
$\textrm{PRA}$
are all provable in
![]() $I\forall _1=I\exists _1$
and hence in
$I\forall _1=I\exists _1$
and hence in
![]() $\textrm{TI}(\forall _1, \prec )$
, as they are actually encoded in the definition
$\textrm{TI}(\forall _1, \prec )$
, as they are actually encoded in the definition
![]() $D_f$
of
$D_f$
of
![]() $f$
. For the quantifier-free induction of
$f$
. For the quantifier-free induction of
![]() $\textrm{PRA}$
, as we have seen before, it is possible to use the isomorphism
$\textrm{PRA}$
, as we have seen before, it is possible to use the isomorphism
![]() $o$
to prove the induction in
$o$
to prove the induction in
![]() $\textrm{TI}(\forall _1, \prec )$
.
$\textrm{TI}(\forall _1, \prec )$
.
Lemma 6.
If
![]() $\textrm{PRA}+\bigcup _{\beta \in \mathcal{O}} \textrm{PRWO}({\prec_{\beta}}) \vdash A$
then
$\textrm{PRA}+\bigcup _{\beta \in \mathcal{O}} \textrm{PRWO}({\prec_{\beta}}) \vdash A$
then
![]() $\textrm{TI}(\forall _1, \prec ) \vdash A$
, for any
$\textrm{TI}(\forall _1, \prec ) \vdash A$
, for any
![]() $A \in \mathcal{L}_{\textrm{PV}}$
.
$A \in \mathcal{L}_{\textrm{PV}}$
.
Proof.
Pretend
![]() $\textrm{TI}(\forall _1, \prec )$
has a function symbol for any primitive recursive function, allowed in the
$\textrm{TI}(\forall _1, \prec )$
has a function symbol for any primitive recursive function, allowed in the
![]() $\forall _1$
-formulas. As
$\forall _1$
-formulas. As
![]() $\textrm{TI}(\forall _1, \prec )$
extends
$\textrm{TI}(\forall _1, \prec )$
extends
![]() $\textrm{PRA}$
, it is enough to prove
$\textrm{PRA}$
, it is enough to prove
![]() $\textrm{TI}(\forall _1, \prec ) \vdash \textrm{PRWO}({\prec_{\beta}})$
, for any
$\textrm{TI}(\forall _1, \prec ) \vdash \textrm{PRWO}({\prec_{\beta}})$
, for any
![]() $\beta \in \mathcal{O}$
. For the sake of contradiction, assume
$\beta \in \mathcal{O}$
. For the sake of contradiction, assume
![]() $\forall y [f(\bar{x}, y+1) \prec f(\bar{x}, y) \wedge \mathcal{O}(f(\bar{x}, y)) \wedge f(\bar{x}, y) \prec \beta ]$
. Set
$\forall y [f(\bar{x}, y+1) \prec f(\bar{x}, y) \wedge \mathcal{O}(f(\bar{x}, y)) \wedge f(\bar{x}, y) \prec \beta ]$
. Set
![]() $B(\gamma, \bar{x})= \forall y (f(\bar{x}, y) \neq \gamma )$
and note that
$B(\gamma, \bar{x})= \forall y (f(\bar{x}, y) \neq \gamma )$
and note that
![]() $B(\gamma, \bar{x}) \in \forall _1$
. By transfinite induction, we prove
$B(\gamma, \bar{x}) \in \forall _1$
. By transfinite induction, we prove
![]() $\forall \gamma \prec \beta \,B(\gamma, \bar{x})$
. For that purpose, assume
$\forall \gamma \prec \beta \,B(\gamma, \bar{x})$
. For that purpose, assume
![]() $\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
. Then, to prove
$\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
. Then, to prove
![]() $[\gamma \prec \beta \to B(\gamma, \bar{x})]$
, if
$[\gamma \prec \beta \to B(\gamma, \bar{x})]$
, if
![]() $f(\bar{x}, y) = \gamma$
, for some
$f(\bar{x}, y) = \gamma$
, for some
![]() $\gamma \prec \beta$
, as
$\gamma \prec \beta$
, as
![]() $f(\bar{x}, y+1) \prec f(\bar{x}, y)$
, we have
$f(\bar{x}, y+1) \prec f(\bar{x}, y)$
, we have
![]() $f(\bar{x}, y+1) \prec \gamma \prec \beta$
. On the other hand, by
$f(\bar{x}, y+1) \prec \gamma \prec \beta$
. On the other hand, by
![]() $\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
, we know that none of the ordinals
$\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
, we know that none of the ordinals
![]() $\delta$
below
$\delta$
below
![]() $\gamma$
is in the form of
$\gamma$
is in the form of
![]() $f(\bar{x}, z)$
, which contradicts with
$f(\bar{x}, z)$
, which contradicts with
![]() $f(\bar{x}, y+1) \prec \gamma$
. Hence,
$f(\bar{x}, y+1) \prec \gamma$
. Hence,
![]() $[\gamma \prec \beta \to B(\gamma, \bar{x})]$
. Therefore,
$[\gamma \prec \beta \to B(\gamma, \bar{x})]$
. Therefore,
![]() $\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
implies
$\forall \delta \prec \gamma [\delta \prec \beta \to B(\delta, \bar{x})]$
implies
![]() $[\gamma \prec \beta \to B(\gamma, \bar{x})]$
. Hence, by transfinite induction, we have
$[\gamma \prec \beta \to B(\gamma, \bar{x})]$
. Hence, by transfinite induction, we have
![]() $\forall \gamma \prec \beta \, B(\gamma, \bar{x})$
which for
$\forall \gamma \prec \beta \, B(\gamma, \bar{x})$
which for
![]() $\gamma =f(\bar{x}, 0) \prec \beta$
implies
$\gamma =f(\bar{x}, 0) \prec \beta$
implies
![]() $\forall y (f(\bar{x}, y) \neq f(\bar{x}, 0))$
which is a contradiction.
$\forall y (f(\bar{x}, y) \neq f(\bar{x}, 0))$
which is a contradiction.
Corollary 7.
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \equiv _{\Pi ^0_2} \textrm{TI}(\forall _1, \prec )$
.
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \equiv _{\Pi ^0_2} \textrm{TI}(\forall _1, \prec )$
.
Proof.
One direction is a consequence of the fact that
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
proves the transfinite induction for any formulas and hence extends the theory
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
proves the transfinite induction for any formulas and hence extends the theory
![]() $\textrm{TI}(\forall _1, \prec )$
. The other direction is a consequence of Theorem 3 and Lemma 6.
$\textrm{TI}(\forall _1, \prec )$
. The other direction is a consequence of Theorem 3 and Lemma 6.
4.1.1 A proof system for
 $\textrm{TI}(\forall _1, \prec )$
$\textrm{TI}(\forall _1, \prec )$
We now present a sequent calculus for the theory
![]() $\textrm{TI}(\forall _1, \prec )$
. By a sequent over
$\textrm{TI}(\forall _1, \prec )$
. By a sequent over
![]() $\mathcal{L}_{\textrm{PV}}$
, we mean an expression in the form
$\mathcal{L}_{\textrm{PV}}$
, we mean an expression in the form
![]() $S=\Gamma \Rightarrow \Delta$
, where
$S=\Gamma \Rightarrow \Delta$
, where
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Delta$
are multisets of formulas in
$\Delta$
are multisets of formulas in
![]() $\mathcal{L}_{\textrm{PV}}$
. Define
$\mathcal{L}_{\textrm{PV}}$
. Define
![]() $\textbf{LPV}$
as the usual system
$\textbf{LPV}$
as the usual system
![]() $\textbf{LK}$
augmented with the equality axioms for atomic formulas and their negations and all quantifier-free theorems of
$\textbf{LK}$
augmented with the equality axioms for atomic formulas and their negations and all quantifier-free theorems of
![]() $\textrm{PV}$
as the initial sequents:
$\textrm{PV}$
as the initial sequents:
Axioms:
where
![]() $P$
ranges over all atomic formulas,
$P$
ranges over all atomic formulas,
![]() $f$
ranges over all function symbols in the language,
$f$
ranges over all function symbols in the language,
![]() $Q$
ranges over all atmoic formulas or their negations, and
$Q$
ranges over all atmoic formulas or their negations, and
![]() $A$
ranges over all quantifier-free theorems of
$A$
ranges over all quantifier-free theorems of
![]() $\textrm{PV}$
.
$\textrm{PV}$
.
Structural Rules:
Logical Rules:
In the rules
![]() $(R\forall )$
and
$(R\forall )$
and
![]() $(L\exists )$
, the variable
$(L\exists )$
, the variable
![]() $y$
should not appear in the consequence. Adding the rule
$y$
should not appear in the consequence. Adding the rule
to
![]() $\textbf{LPV}$
, we get
$\textbf{LPV}$
, we get
![]() $\textbf{G}_0$
. Note that in
$\textbf{G}_0$
. Note that in
![]() $(Ind_{\alpha })$
, the variable
$(Ind_{\alpha })$
, the variable
![]() $\delta$
should not appear in the consequence. Moreover, the constant
$\delta$
should not appear in the consequence. Moreover, the constant
![]() $\theta \in \mathcal{O}$
is arbitrary and can take any value. For more on the proof theory of first-order theories and specially arithmetic, see Buss (Reference Buss1998a,Reference Bussb).
$\theta \in \mathcal{O}$
is arbitrary and can take any value. For more on the proof theory of first-order theories and specially arithmetic, see Buss (Reference Buss1998a,Reference Bussb).
By the usual cut reduction method (Buss Reference Buss1998a,Reference Bussb), it is easy to prove that for any
![]() $\Gamma \cup \Delta \subseteq \forall _1$
, if
$\Gamma \cup \Delta \subseteq \forall _1$
, if
![]() $\Gamma \Rightarrow \Delta$
is provable in
$\Gamma \Rightarrow \Delta$
is provable in
![]() $\textrm{TI}(\forall _1, \prec )$
(resp.,
$\textrm{TI}(\forall _1, \prec )$
(resp.,
![]() $\textrm{PV}$
), then it has a
$\textrm{PV}$
), then it has a
![]() $\textbf{G}_0$
-proof (resp.
$\textbf{G}_0$
-proof (resp.
![]() $\textbf{LPV}$
-proof) consisting only of
$\textbf{LPV}$
-proof) consisting only of
![]() $\forall _1$
-formulas. For some practical reasons, we simplify the system
$\forall _1$
-formulas. For some practical reasons, we simplify the system
![]() $\textbf{G}_0$
by changing the cut and the induction rules to the weak cut and weak induction rules, respectively:
$\textbf{G}_0$
by changing the cut and the induction rules to the weak cut and weak induction rules, respectively:
Denote this system by
![]() $\textbf{G}_1$
. Note that the difference between
$\textbf{G}_1$
. Note that the difference between
![]() $(Ind_{\alpha })$
and
$(Ind_{\alpha })$
and
![]() $(wInd_{\alpha })$
is that in the latter
$(wInd_{\alpha })$
is that in the latter
![]() $\Delta$
is omitted and
$\Delta$
is omitted and
![]() $A(\delta )$
is replaced by
$A(\delta )$
is replaced by
![]() $\forall \gamma \prec \delta +1 \; A(\gamma )$
.
$\forall \gamma \prec \delta +1 \; A(\gamma )$
.
Lemma 8.
For any
![]() $\Gamma \cup \Delta \subseteq \forall _1$
, if
$\Gamma \cup \Delta \subseteq \forall _1$
, if
![]() $\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
$\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
![]() $\Gamma \Rightarrow \Delta$
has a
$\Gamma \Rightarrow \Delta$
has a
![]() $\textbf{G}_1$
-proof only consisting of
$\textbf{G}_1$
-proof only consisting of
![]() $\forall _1$
-formulas.
$\forall _1$
-formulas.
Proof.
By a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{G}_1$
(resp.
$\textbf{G}_1$
(resp.
![]() $\textbf{LPV}$
), we mean a proof in
$\textbf{LPV}$
), we mean a proof in
![]() $\textbf{G}_1$
(resp.
$\textbf{G}_1$
(resp.
![]() $\textbf{LPV}$
) consisting only of
$\textbf{LPV}$
) consisting only of
![]() $\forall _1$
-formulas. We show that the cut rule and the induction rule (over
$\forall _1$
-formulas. We show that the cut rule and the induction rule (over
![]() $\forall _1$
-formulas) are derivable in
$\forall _1$
-formulas) are derivable in
![]() $\textbf{G}_1$
(by a
$\textbf{G}_1$
(by a
![]() $\forall _1$
-proof). We only investigate the harder case of
$\forall _1$
-proof). We only investigate the harder case of
![]() $\forall _1$
-proofs. The other is the same omitting the restrictions everywhere.
$\forall _1$
-proofs. The other is the same omitting the restrictions everywhere.
For cut, consider the following proof-tree in
![]() $\textbf{G}_1$
, where the double lines mean simple omitted proofs in
$\textbf{G}_1$
, where the double lines mean simple omitted proofs in
![]() $\textbf{G}_1$
. The tree proves
$\textbf{G}_1$
. The tree proves
![]() $\Gamma, \Sigma \Rightarrow \Lambda, \Delta$
from
$\Gamma, \Sigma \Rightarrow \Lambda, \Delta$
from
![]() $\Gamma \Rightarrow A, \Delta$
and
$\Gamma \Rightarrow A, \Delta$
and
![]() $\Sigma, A \Rightarrow \Lambda$
.
$\Sigma, A \Rightarrow \Lambda$
.

Note that the simulation of the cut rule in
![]() $\textbf{G}_1$
implies that
$\textbf{G}_1$
implies that
![]() $\textbf{G}_1$
is as powerful as
$\textbf{G}_1$
is as powerful as
![]() $\textbf{LPV}$
. It also transforms a
$\textbf{LPV}$
. It also transforms a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{LPV}$
to a
$\textbf{LPV}$
to a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{G}_1$
. For the induction rule, consider the following proof-tree proving
$\textbf{G}_1$
. For the induction rule, consider the following proof-tree proving
![]() $\Gamma \Rightarrow A(\theta ), \Delta$
from
$\Gamma \Rightarrow A(\theta ), \Delta$
from
![]() $\Gamma, \forall \gamma \prec \delta \; A(\gamma ) \Rightarrow A(\delta ), \Delta$
:
$\Gamma, \forall \gamma \prec \delta \; A(\gamma ) \Rightarrow A(\delta ), \Delta$
:

where
![]() $(*)$
is the result of a cut with the sequent
$(*)$
is the result of a cut with the sequent
![]() $\forall \gamma \prec \delta \, [A(\gamma ) \vee \bigvee \Delta ] \Rightarrow [\forall \gamma \prec \delta \; A(\gamma )] \vee \bigvee \Delta$
which has a proof in
$\forall \gamma \prec \delta \, [A(\gamma ) \vee \bigvee \Delta ] \Rightarrow [\forall \gamma \prec \delta \; A(\gamma )] \vee \bigvee \Delta$
which has a proof in
![]() $\textbf{LPV}$
and hence a
$\textbf{LPV}$
and hence a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{LPV}$
and by the observation we have just made, a
$\textbf{LPV}$
and by the observation we have just made, a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{G}_1$
. Note that the use of cut is allowed as we showed its derivability in
$\textbf{G}_1$
. Note that the use of cut is allowed as we showed its derivability in
![]() $\textbf{G}_1$
. Moreover,
$\textbf{G}_1$
. Moreover,
![]() $(**)$
is the result of a cut with the
$(**)$
is the result of a cut with the
![]() $\textrm{PV}$
-provable sequent
$\textrm{PV}$
-provable sequent
![]() $[A(\delta ) \vee \bigvee \Delta ], \forall \gamma \prec \delta \, [A(\gamma ) \vee \bigvee \Delta ] \Rightarrow \forall \gamma \prec \delta +1 \, [A(\gamma ) \vee \bigvee \Delta ]$
. The latter is provable in
$[A(\delta ) \vee \bigvee \Delta ], \forall \gamma \prec \delta \, [A(\gamma ) \vee \bigvee \Delta ] \Rightarrow \forall \gamma \prec \delta +1 \, [A(\gamma ) \vee \bigvee \Delta ]$
. The latter is provable in
![]() $\textbf{LPV}$
. Therefore, it has a
$\textbf{LPV}$
. Therefore, it has a
![]() $\forall _1$
-proof in
$\forall _1$
-proof in
![]() $\textbf{LPV}$
and hence in
$\textbf{LPV}$
and hence in
![]() $\textbf{G}_1$
. Finally,
$\textbf{G}_1$
. Finally,
![]() $\dagger$
is the result of a cut with
$\dagger$
is the result of a cut with
![]() $ A(\theta ) \vee \bigvee \Delta \Rightarrow A(\theta ), \Delta$
that has a trivial
$ A(\theta ) \vee \bigvee \Delta \Rightarrow A(\theta ), \Delta$
that has a trivial
![]() $\forall _1$
-proof.
$\forall _1$
-proof.
4.2 Ordinal flows
In this subsection, we will witness
![]() $\textrm{TI}(\forall _1, \prec )$
-provable implications between
$\textrm{TI}(\forall _1, \prec )$
-provable implications between
![]() $\forall _1$
-formulas by a sequence of
$\forall _1$
-formulas by a sequence of
![]() $\beta$
many
$\beta$
many
![]() $\textrm{PV}$
-provable implications, for some
$\textrm{PV}$
-provable implications, for some
![]() $\beta \in \mathcal{O}$
.
$\beta \in \mathcal{O}$
.
Definition 9.
Let
![]() $A(\bar{x}), B(\bar{x}) \in \forall _1$
. A pair
$A(\bar{x}), B(\bar{x}) \in \forall _1$
. A pair
![]() $(H(\gamma, \bar{x}), \beta )$
of a
$(H(\gamma, \bar{x}), \beta )$
of a
![]() $\forall _1$
-formula and
$\forall _1$
-formula and
![]() $\beta \in \mathcal{O}$
such that
$\beta \in \mathcal{O}$
such that
![]() $\beta \succeq 1$
is called an
$\beta \succeq 1$
is called an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
, if:
$B(\bar{x})$
, if:
-
•
 $\textrm{PV} \vdash A(\bar{x}) \leftrightarrow H(0, \bar{x})$
.
$\textrm{PV} \vdash A(\bar{x}) \leftrightarrow H(0, \bar{x})$
. -
•
 $\textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
.
$\textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
. -
•
 $\textrm{PV} \vdash H(\beta, \bar{x}) \leftrightarrow B(\bar{x})$
.
$\textrm{PV} \vdash H(\beta, \bar{x}) \leftrightarrow B(\bar{x})$
.
We denote the existence of an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
by
$B(\bar{x})$
by
![]() $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
. For any multisets
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
. For any multisets
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Delta$
of
$\Delta$
of
![]() $\forall _1$
-formulas, by
$\forall _1$
-formulas, by
![]() $\Gamma \rhd _{\alpha } \Delta$
, we mean
$\Gamma \rhd _{\alpha } \Delta$
, we mean
![]() $\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta$
.
$\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta$
.
In order to use
![]() $\alpha$
-flows to witness the proofs in
$\alpha$
-flows to witness the proofs in
![]() $\textrm{TI}(\forall _1, \prec )$
, we will develop a high-level calculus for this new notion, implemented in the following series of lemmas.
$\textrm{TI}(\forall _1, \prec )$
, we will develop a high-level calculus for this new notion, implemented in the following series of lemmas.
Lemma 10.
Let
![]() $A(\bar{x}), B(\bar{x}), C(\bar{x}) \in \forall _1$
. Then:
$A(\bar{x}), B(\bar{x}), C(\bar{x}) \in \forall _1$
. Then:
-
(i) If
 $\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, then
$\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, then
 $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
.
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
. -
(ii) If
 $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, then
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, then
 $A(\bar{x}) \circ C(\bar{x}) \rhd _{\alpha } B(\bar{x}) \circ C(\bar{x})$
, for any
$A(\bar{x}) \circ C(\bar{x}) \rhd _{\alpha } B(\bar{x}) \circ C(\bar{x})$
, for any
 $\circ \in \{\wedge, \vee \}$
.
$\circ \in \{\wedge, \vee \}$
.
Proof.
For
![]() $(i)$
, set
$(i)$
, set
![]() $\beta =1$
and
$\beta =1$
and
![]() $H(\gamma, \bar{x})=(\gamma =0 \to A(\bar{x})) \wedge (\gamma =1 \to B(\bar{x}))$
. It is clear that
$H(\gamma, \bar{x})=(\gamma =0 \to A(\bar{x})) \wedge (\gamma =1 \to B(\bar{x}))$
. It is clear that
![]() $\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow A(\bar{x})$
and
$\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow A(\bar{x})$
and
![]() $\textrm{PV} \vdash H(1, \bar{x}) \leftrightarrow B(\bar{x})$
. As
$\textrm{PV} \vdash H(1, \bar{x}) \leftrightarrow B(\bar{x})$
. As
![]() $\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, we can see that
$\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, we can see that
![]() $(H(\gamma, \bar{x}), \beta )$
is an
$(H(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
.
$B(\bar{x})$
.
For
![]() $(ii)$
, we only prove the conjunction case. The disjunction case is similar. Since
$(ii)$
, we only prove the conjunction case. The disjunction case is similar. Since
![]() $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, by Definition 9, there exist an ordinal
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, by Definition 9, there exist an ordinal
![]() $\beta \succeq 1$
and a formula
$\beta \succeq 1$
and a formula
![]() $H(\gamma, \bar{x}) \in \forall _1$
satisfying the conditions in Definition 9. Set
$H(\gamma, \bar{x}) \in \forall _1$
satisfying the conditions in Definition 9. Set
![]() $I(\gamma, \bar{x})=H(\gamma, \bar{x}) \wedge C(\bar{x})$
and note that
$I(\gamma, \bar{x})=H(\gamma, \bar{x}) \wedge C(\bar{x})$
and note that
![]() $I(\gamma, \bar{x}) \in \forall _1$
. It is easy to see that the pair
$I(\gamma, \bar{x}) \in \forall _1$
. It is easy to see that the pair
![]() $(I(\gamma, \bar{x}), \beta )$
is an
$(I(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $A(\bar{x}) \wedge C(\bar{x})$
to
$A(\bar{x}) \wedge C(\bar{x})$
to
![]() $B(\bar{x}) \wedge C(\bar{x})$
, as the
$B(\bar{x}) \wedge C(\bar{x})$
, as the
![]() $\textrm{PV}$
-provability of
$\textrm{PV}$
-provability of
![]() $\forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
implies the
$\forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
implies the
![]() $\textrm{PV}$
-provability of
$\textrm{PV}$
-provability of
![]() $\forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; (H(\gamma, \bar{x}) \wedge C(\bar{x})) \rightarrow (H(\delta, \bar{x}) \wedge C(\bar{x}))]$
.
$\forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; (H(\gamma, \bar{x}) \wedge C(\bar{x})) \rightarrow (H(\delta, \bar{x}) \wedge C(\bar{x}))]$
.
In the next lemma, we glue
![]() $\alpha$
-flows together to construct longer
$\alpha$
-flows together to construct longer
![]() $\alpha$
-flows. Notice that the proof heavily uses the fact that the operations
$\alpha$
-flows. Notice that the proof heavily uses the fact that the operations
![]() $\{+, \dot{-}, \cdot, d\}$
and their basic properties are representable in
$\{+, \dot{-}, \cdot, d\}$
and their basic properties are representable in
![]() $\textrm{PV}$
.
$\textrm{PV}$
.
Lemma 11.
-
(i) If
 $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
and
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
and
 $ B(\bar{x}) \rhd _{\alpha } C(\bar{x})$
, then
$ B(\bar{x}) \rhd _{\alpha } C(\bar{x})$
, then
 $A(\bar{x}) \rhd _{\alpha } C(\bar{x})$
.
$A(\bar{x}) \rhd _{\alpha } C(\bar{x})$
. -
(ii) If
 $\Gamma, \forall \gamma \prec \delta \; A(\gamma, \bar{x}) \rhd _{\alpha } \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
, then
$\Gamma, \forall \gamma \prec \delta \; A(\gamma, \bar{x}) \rhd _{\alpha } \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
, then
 $\Gamma \rhd _{\alpha } A(\theta, \bar{x})$
, for any
$\Gamma \rhd _{\alpha } A(\theta, \bar{x})$
, for any
 $\theta \in \mathcal{O}$
.
$\theta \in \mathcal{O}$
.
Proof.
For
![]() $(i)$
, as
$(i)$
, as
![]() $A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, there exists an
$A(\bar{x}) \rhd _{\alpha } B(\bar{x})$
, there exists an
![]() $\alpha$
-flow
$\alpha$
-flow
![]() $(H(\gamma, \bar{x}), \beta )$
from
$(H(\gamma, \bar{x}), \beta )$
from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
. Similarly, as
$B(\bar{x})$
. Similarly, as
![]() $B(\bar{x}) \rhd _{\alpha } C(\bar{x})$
, there is an
$B(\bar{x}) \rhd _{\alpha } C(\bar{x})$
, there is an
![]() $\alpha$
-flow
$\alpha$
-flow
![]() $(H'(\gamma, \bar{x}), \beta ')$
from
$(H'(\gamma, \bar{x}), \beta ')$
from
![]() $B(\bar{x})$
to
$B(\bar{x})$
to
![]() $C(\bar{x})$
. Set
$C(\bar{x})$
. Set
![]() $\beta ''=\beta +\beta '$
and
$\beta ''=\beta +\beta '$
and
![]() $H''(\gamma, \bar{x})=[\gamma \preceq \beta \to H(\gamma, \bar{x})] \wedge [\beta \prec \gamma \preceq \beta +\beta ' \to H'(\gamma \dot{-} \beta, \bar{x})]$
. We claim that the pair
$H''(\gamma, \bar{x})=[\gamma \preceq \beta \to H(\gamma, \bar{x})] \wedge [\beta \prec \gamma \preceq \beta +\beta ' \to H'(\gamma \dot{-} \beta, \bar{x})]$
. We claim that the pair
![]() $(H''(\gamma, \bar{x}), \beta '')$
is an
$(H''(\gamma, \bar{x}), \beta '')$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $C(\bar{x})$
. First, note that
$C(\bar{x})$
. First, note that
![]() $H''(0, \bar{x})$
is
$H''(0, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, \bar{x})$
which is
$H(0, \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $A(\bar{x})$
. Similarly, as
$A(\bar{x})$
. Similarly, as
![]() $(\beta +\beta ')\dot{-} \beta =\beta '$
is provable in
$(\beta +\beta ')\dot{-} \beta =\beta '$
is provable in
![]() $\textrm{PV}$
, we know that
$\textrm{PV}$
, we know that
![]() $H''(\beta +\beta ', \bar{x})$
is
$H''(\beta +\beta ', \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H'(\beta ', \bar{x})$
which is
$H'(\beta ', \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $C(\bar{x})$
. To prove
$C(\bar{x})$
. To prove
![]() $ \textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta '' \; [\forall \gamma \prec \delta \; H''(\gamma, \bar{x}) \rightarrow H''(\delta, \bar{x})],$
note that if
$ \textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta '' \; [\forall \gamma \prec \delta \; H''(\gamma, \bar{x}) \rightarrow H''(\delta, \bar{x})],$
note that if
![]() $\delta \preceq \beta$
, then the claim reduces to the same claim for
$\delta \preceq \beta$
, then the claim reduces to the same claim for
![]() $H(\gamma, \bar{x})$
which is provable. If
$H(\gamma, \bar{x})$
which is provable. If
![]() $\beta \prec \delta \preceq \beta +\beta '$
, assume
$\beta \prec \delta \preceq \beta +\beta '$
, assume
![]() $\forall \gamma \prec \delta \; H''(\gamma, \bar{x})$
to prove
$\forall \gamma \prec \delta \; H''(\gamma, \bar{x})$
to prove
![]() $H''(\delta, \bar{x})$
or equivalently
$H''(\delta, \bar{x})$
or equivalently
![]() $H'(\delta \dot{-} \beta, \bar{x})$
. Note that
$H'(\delta \dot{-} \beta, \bar{x})$
. Note that
![]() $\forall \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
$\forall \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
![]() $\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
. As the interval
$\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
. As the interval
![]() $(0, \delta \dot{-} \beta )$
is isomorphic to
$(0, \delta \dot{-} \beta )$
is isomorphic to
![]() $(\beta, \delta )$
, by the map
$(\beta, \delta )$
, by the map
![]() $\gamma \mapsto \beta +\gamma$
, then
$\gamma \mapsto \beta +\gamma$
, then
![]() $\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
$\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
![]() $\forall 0 \prec \gamma \prec \delta \dot{-} \beta \; H''(\beta +\gamma, \bar{x})$
which implies
$\forall 0 \prec \gamma \prec \delta \dot{-} \beta \; H''(\beta +\gamma, \bar{x})$
which implies
![]() $\forall 0 \prec \gamma \prec \delta \dot{-} \beta \; H'(\gamma, \bar{x})$
. On the other hand,
$\forall 0 \prec \gamma \prec \delta \dot{-} \beta \; H'(\gamma, \bar{x})$
. On the other hand,
![]() $\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
$\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
![]() $H''(\beta, \bar{x})$
which is
$H''(\beta, \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(\beta, \bar{x})$
, by definition. As
$H(\beta, \bar{x})$
, by definition. As
![]() $H(\beta, \bar{x})$
is
$H(\beta, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(\bar{x})$
which is also
$B(\bar{x})$
which is also
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H'(0, \bar{x})$
, we can claim that
$H'(0, \bar{x})$
, we can claim that
![]() $H(\beta, \bar{x})$
and
$H(\beta, \bar{x})$
and
![]() $H'(0, \bar{x})$
are
$H'(0, \bar{x})$
are
![]() $\textrm{PV}$
-equivalent. Hence,
$\textrm{PV}$
-equivalent. Hence,
![]() $\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
$\forall \beta \preceq \gamma \prec \delta \; H''(\gamma, \bar{x})$
implies
![]() $\forall \gamma \prec \delta \dot{-} \beta \; H'(\gamma, \bar{x})$
which also implies
$\forall \gamma \prec \delta \dot{-} \beta \; H'(\gamma, \bar{x})$
which also implies
![]() $H'(\delta \dot{-} \beta, \bar{x})$
, as
$H'(\delta \dot{-} \beta, \bar{x})$
, as
![]() $(H'(\gamma, \bar{x}), \beta ')$
is an
$(H'(\gamma, \bar{x}), \beta ')$
is an
![]() $\alpha$
-flow.
$\alpha$
-flow.
For
![]() $(ii)$
, as
$(ii)$
, as
![]() $\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x}) \rhd _{\alpha } \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
, by Lemma 10, we have
$\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x}) \rhd _{\alpha } \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
, by Lemma 10, we have
![]() $\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x}) \rhd _{\alpha } \bigwedge \Gamma \wedge \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
. Set
$\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x}) \rhd _{\alpha } \bigwedge \Gamma \wedge \forall \gamma \prec \delta +1 \; A(\gamma, \bar{x})$
. Set
![]() $B(\delta, \bar{x})=\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x})$
. Therefore,
$B(\delta, \bar{x})=\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x})$
. Therefore,
![]() $B(\delta, \bar{x}) \rhd _{\alpha } B(\delta +1, \bar{x})$
. Let
$B(\delta, \bar{x}) \rhd _{\alpha } B(\delta +1, \bar{x})$
. Let
![]() $(H(\eta, \delta, \bar{x}), \beta )$
be the
$(H(\eta, \delta, \bar{x}), \beta )$
be the
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $B(\delta, \bar{x})$
to
$B(\delta, \bar{x})$
to
![]() $B(\delta +1, \bar{x})$
. Note that
$B(\delta +1, \bar{x})$
. Note that
![]() $H(0, \delta, \bar{x})$
is
$H(0, \delta, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(\delta,\bar{x})$
and
$B(\delta,\bar{x})$
and
![]() $H(\beta, \delta, \bar{x})$
is
$H(\beta, \delta, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, \delta +1, \bar{x})$
, as both are
$H(0, \delta +1, \bar{x})$
, as both are
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(\delta +1)$
. Define
$B(\delta +1)$
. Define
![]() $\beta '=\beta (\theta +1)$
and
$\beta '=\beta (\theta +1)$
and
![]() $I(\tau, \bar{x})=H(\tau \dot{-} \beta d(\tau, \beta ), d(\tau, \beta ), \bar{x})$
and note that
$I(\tau, \bar{x})=H(\tau \dot{-} \beta d(\tau, \beta ), d(\tau, \beta ), \bar{x})$
and note that
![]() $I(\tau, \bar{x}) \in \forall _1$
. We show that
$I(\tau, \bar{x}) \in \forall _1$
. We show that
![]() $(I(\tau, \bar{x}), \beta ')$
is an
$(I(\tau, \bar{x}), \beta ')$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $B(0, \bar{x})$
to
$B(0, \bar{x})$
to
![]() $B(\theta +1, \bar{x})$
. Note that
$B(\theta +1, \bar{x})$
. Note that
![]() $(I(\tau, \bar{x}), \beta ')$
is nothing but the result of gluing the
$(I(\tau, \bar{x}), \beta ')$
is nothing but the result of gluing the
![]() $\alpha$
-flows
$\alpha$
-flows
![]() $(H(\eta, \delta, \bar{x}), \beta )$
, for all
$(H(\eta, \delta, \bar{x}), \beta )$
, for all
![]() $\delta \prec \theta +1$
, one after another as depicted in the following figure (for simplicity, in the figures, we drop the free variables
$\delta \prec \theta +1$
, one after another as depicted in the following figure (for simplicity, in the figures, we drop the free variables
![]() $\bar{x}$
).
$\bar{x}$
).

First, as
![]() $d(0,\beta )=0$
and
$d(0,\beta )=0$
and
![]() $0 \dot{-} \beta d(0,\beta )=0$
, provably in
$0 \dot{-} \beta d(0,\beta )=0$
, provably in
![]() $\textrm{PV}$
, we know that
$\textrm{PV}$
, we know that
![]() $I(0, \bar{x})$
is
$I(0, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, 0, \bar{x})$
which is itself
$H(0, 0, \bar{x})$
which is itself
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(0, \bar{x})$
. Second, as
$B(0, \bar{x})$
. Second, as
![]() $d(\beta (\theta +1), \beta )=\theta +1$
and
$d(\beta (\theta +1), \beta )=\theta +1$
and
![]() $\beta (\theta +1) \dot{-} \beta d(\beta (\theta +1), \beta )=0$
, provably in
$\beta (\theta +1) \dot{-} \beta d(\beta (\theta +1), \beta )=0$
, provably in
![]() $\textrm{PV}$
, we know that
$\textrm{PV}$
, we know that
![]() $I(\beta (\theta +1), \bar{x})$
is
$I(\beta (\theta +1), \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, \theta +1, \bar{x})$
which is
$H(0, \theta +1, \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(\theta +1, \bar{x})$
. For the middle condition, we must prove
$B(\theta +1, \bar{x})$
. For the middle condition, we must prove
![]() $ \textrm{PV} \vdash \forall \; 1 \preceq \tau \preceq \beta (\theta +1) \; [\forall \zeta \prec \tau \; I(\zeta, \bar{x}) \rightarrow I(\tau, \bar{x})]$
. There are two cases to consider, either
$ \textrm{PV} \vdash \forall \; 1 \preceq \tau \preceq \beta (\theta +1) \; [\forall \zeta \prec \tau \; I(\zeta, \bar{x}) \rightarrow I(\tau, \bar{x})]$
. There are two cases to consider, either
![]() $\beta d(\tau, \beta ) \prec \tau$
or
$\beta d(\tau, \beta ) \prec \tau$
or
![]() $\beta d(\tau, \beta )= \tau$
. If
$\beta d(\tau, \beta )= \tau$
. If
![]() $\beta d(\tau, \beta ) \prec \tau$
, then
$\beta d(\tau, \beta ) \prec \tau$
, then
![]() $\beta d(\tau, \beta )+1 \preceq \tau$
which implies
$\beta d(\tau, \beta )+1 \preceq \tau$
which implies
![]() $\tau =\beta d(\tau, \beta )+\mu$
for
$\tau =\beta d(\tau, \beta )+\mu$
for
![]() $\mu =\tau \dot{-} \beta d(\tau, \beta ) \succeq 1$
. As for any
$\mu =\tau \dot{-} \beta d(\tau, \beta ) \succeq 1$
. As for any
![]() $\eta \prec \mu$
, we have
$\eta \prec \mu$
, we have
![]() $\beta d(\tau, \beta ) + \eta \prec \tau$
, we know that
$\beta d(\tau, \beta ) + \eta \prec \tau$
, we know that
![]() $\forall \zeta \prec \tau \; I(\zeta, \bar{x})$
implies
$\forall \zeta \prec \tau \; I(\zeta, \bar{x})$
implies
![]() $\forall \eta \prec \mu \; H(\eta, d(\tau, \beta ), \bar{x})$
. As we have
$\forall \eta \prec \mu \; H(\eta, d(\tau, \beta ), \bar{x})$
. As we have
![]() $\mu \succeq 1$
, the latter proves
$\mu \succeq 1$
, the latter proves
![]() $H(\mu, d(\tau, \beta ), \bar{x})$
which is
$H(\mu, d(\tau, \beta ), \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $I(\tau, \bar{x})$
.
$I(\tau, \bar{x})$
.

For the other case, if
![]() $\beta d(\tau, \beta )=\tau$
, we should use
$\beta d(\tau, \beta )=\tau$
, we should use
![]() $\forall \zeta \prec \tau \; I(\zeta, \bar{x})$
to prove the formula
$\forall \zeta \prec \tau \; I(\zeta, \bar{x})$
to prove the formula
![]() $I(\tau, \bar{x})=H(0, d(\tau, \beta ), \bar{x})$
. Again, there are two cases to consider: either
$I(\tau, \bar{x})=H(0, d(\tau, \beta ), \bar{x})$
. Again, there are two cases to consider: either
![]() $d(\tau, \beta )$
is a successor or a limit ordinal. If
$d(\tau, \beta )$
is a successor or a limit ordinal. If
![]() $d(\tau, \beta )=\rho +1$
, for some
$d(\tau, \beta )=\rho +1$
, for some
![]() $\rho$
, as
$\rho$
, as
![]() $H(0, \rho +1, \bar{x})$
is
$H(0, \rho +1, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(\beta, \rho, \bar{x})$
, it is enough to prove
$H(\beta, \rho, \bar{x})$
, it is enough to prove
![]() $H(\beta, \rho, \bar{x})$
. As
$H(\beta, \rho, \bar{x})$
. As
![]() $\beta \rho +\eta \prec \beta \rho +\beta =\beta (\rho +1)=\tau$
, for any
$\beta \rho +\eta \prec \beta \rho +\beta =\beta (\rho +1)=\tau$
, for any
![]() $\eta \prec \beta$
, we know that
$\eta \prec \beta$
, we know that
![]() $\forall \zeta \prec \tau \, I(\zeta, \bar{x})$
implies
$\forall \zeta \prec \tau \, I(\zeta, \bar{x})$
implies
![]() $\forall \eta \prec \beta \, H(\eta, \rho, \bar{x})$
which implies
$\forall \eta \prec \beta \, H(\eta, \rho, \bar{x})$
which implies
![]() $H(\beta, \rho, \bar{x})$
.
$H(\beta, \rho, \bar{x})$
.

If
![]() $d(\tau, \beta )$
is a limit ordinal, then
$d(\tau, \beta )$
is a limit ordinal, then
![]() $\forall \zeta \prec \beta d(\tau, \beta ) \, I(\zeta, \bar{x})$
implies the formula
$\forall \zeta \prec \beta d(\tau, \beta ) \, I(\zeta, \bar{x})$
implies the formula
![]() $\forall \delta \prec d(\tau, \beta ) \, H(0, \delta, \bar{x})$
which implies
$\forall \delta \prec d(\tau, \beta ) \, H(0, \delta, \bar{x})$
which implies
![]() $\forall \delta \prec d(\tau, \beta ) B(\delta, \bar{x})$
. The latter is
$\forall \delta \prec d(\tau, \beta ) B(\delta, \bar{x})$
. The latter is
![]() $\forall \delta \prec d(\tau, \beta ) [\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x})]$
that implies
$\forall \delta \prec d(\tau, \beta ) [\bigwedge \Gamma \wedge \forall \gamma \prec \delta \, A(\gamma, \bar{x})]$
that implies
![]() $\bigwedge \Gamma \wedge \forall \gamma \prec d(\tau, \beta ) \; A(\gamma, \bar{x})$
, as
$\bigwedge \Gamma \wedge \forall \gamma \prec d(\tau, \beta ) \; A(\gamma, \bar{x})$
, as
![]() $d(\tau, \beta )$
is a limit ordinal. The latter is
$d(\tau, \beta )$
is a limit ordinal. The latter is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, d(\tau, \beta ), \bar{x})=I(\tau, \bar{x})$
. This completes the proof of the claim and shows that
$H(0, d(\tau, \beta ), \bar{x})=I(\tau, \bar{x})$
. This completes the proof of the claim and shows that
![]() $B(0, \bar{x}) \rhd _{\alpha } B(\theta +1, \bar{x})$
. Now, as
$B(0, \bar{x}) \rhd _{\alpha } B(\theta +1, \bar{x})$
. Now, as
![]() $\textrm{PV} \vdash \bigwedge \Gamma \to (\bigwedge \Gamma \wedge \forall \gamma \prec 0 \; A(\gamma, \bar{x}))$
and
$\textrm{PV} \vdash \bigwedge \Gamma \to (\bigwedge \Gamma \wedge \forall \gamma \prec 0 \; A(\gamma, \bar{x}))$
and
![]() $\textrm{PV} \vdash (\bigwedge \Gamma \wedge \forall \gamma \prec \theta +1 \; A(\gamma, \bar{x})) \to A(\theta, \bar{x})$
, by Lemma 10, we have
$\textrm{PV} \vdash (\bigwedge \Gamma \wedge \forall \gamma \prec \theta +1 \; A(\gamma, \bar{x})) \to A(\theta, \bar{x})$
, by Lemma 10, we have
![]() $\bigwedge \Gamma \rhd _{\alpha } \bigwedge \Gamma \wedge \forall \gamma \prec 0 \; A(\gamma, \bar{x})$
and
$\bigwedge \Gamma \rhd _{\alpha } \bigwedge \Gamma \wedge \forall \gamma \prec 0 \; A(\gamma, \bar{x})$
and
![]() $\bigwedge \Gamma \wedge \forall \gamma \prec \theta +1 \; A(\gamma, \bar{x}) \rhd _{\alpha } A(\theta, \bar{x})$
. Hence, by part
$\bigwedge \Gamma \wedge \forall \gamma \prec \theta +1 \; A(\gamma, \bar{x}) \rhd _{\alpha } A(\theta, \bar{x})$
. Hence, by part
![]() $(i)$
, we have
$(i)$
, we have
![]() $\bigwedge \Gamma \rhd _{\alpha } A(\theta, \bar{x})$
which completes the proof.
$\bigwedge \Gamma \rhd _{\alpha } A(\theta, \bar{x})$
which completes the proof.
Lemma 12. (Conjunction and Disjunction Rules)
-
(i) If
 $\Gamma, A \rhd _{\alpha } \Delta$
or
$\Gamma, A \rhd _{\alpha } \Delta$
or
 $\Gamma, B \rhd _{\alpha } \Delta$
, then
$\Gamma, B \rhd _{\alpha } \Delta$
, then
 $\Gamma, A \wedge B \rhd _{\alpha } \Delta$
.
$\Gamma, A \wedge B \rhd _{\alpha } \Delta$
. -
(ii) If
 $\Gamma \rhd _{\alpha } A, \Delta$
and
$\Gamma \rhd _{\alpha } A, \Delta$
and
 $\Gamma \rhd _{\alpha } B, \Delta$
, then
$\Gamma \rhd _{\alpha } B, \Delta$
, then
 $\Gamma \rhd _{\alpha } A \wedge B, \Delta$
.
$\Gamma \rhd _{\alpha } A \wedge B, \Delta$
. -
(iii) If
 $\Gamma \rhd _{\alpha } A, \Delta$
or
$\Gamma \rhd _{\alpha } A, \Delta$
or
 $\Gamma \rhd _{\alpha } B, \Delta$
, then
$\Gamma \rhd _{\alpha } B, \Delta$
, then
 $\Gamma \rhd _{\alpha } A \vee B, \Delta$
.
$\Gamma \rhd _{\alpha } A \vee B, \Delta$
. -
(iv) If
 $\Gamma, A \rhd _{\alpha } \Delta$
and
$\Gamma, A \rhd _{\alpha } \Delta$
and
 $\Gamma, B \rhd _{\alpha } \Delta$
, then
$\Gamma, B \rhd _{\alpha } \Delta$
, then
 $\Gamma, A \vee B \rhd _{\alpha } \Delta$
.
$\Gamma, A \vee B \rhd _{\alpha } \Delta$
.
Proof.
For
![]() $(i)$
and
$(i)$
and
![]() $(iii)$
, as the implications
$(iii)$
, as the implications
![]() $[(\bigwedge \Gamma \wedge (A \wedge B)) \to (\bigwedge \Gamma \wedge A)]$
,
$[(\bigwedge \Gamma \wedge (A \wedge B)) \to (\bigwedge \Gamma \wedge A)]$
,
![]() $[(\bigwedge \Gamma \wedge (A \wedge B)) \to (\bigwedge \Gamma \wedge B)]$
,
$[(\bigwedge \Gamma \wedge (A \wedge B)) \to (\bigwedge \Gamma \wedge B)]$
,
![]() $[(\bigvee \Delta \vee A) \to (\bigvee \Delta \vee (A \vee B))]$
and
$[(\bigvee \Delta \vee A) \to (\bigvee \Delta \vee (A \vee B))]$
and
![]() $[(\bigvee \Delta \vee B) \to (\bigvee \Delta \vee (A \vee B))]$
are all provable in
$[(\bigvee \Delta \vee B) \to (\bigvee \Delta \vee (A \vee B))]$
are all provable in
![]() $\textrm{PV}$
, using Lemmas 10 and 11, we reach what we wanted. For
$\textrm{PV}$
, using Lemmas 10 and 11, we reach what we wanted. For
![]() $(ii)$
, if
$(ii)$
, if
![]() $\Gamma \rhd _{\alpha } \Delta, A$
then
$\Gamma \rhd _{\alpha } \Delta, A$
then
![]() $\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee A$
, by definition. By Lemma 10, we reach
$\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee A$
, by definition. By Lemma 10, we reach
![]() $\bigwedge \Gamma \rhd _{\alpha } (\bigvee \Delta \vee A) \wedge \bigwedge \Gamma$
. Similarly, we have
$\bigwedge \Gamma \rhd _{\alpha } (\bigvee \Delta \vee A) \wedge \bigwedge \Gamma$
. Similarly, we have
![]() $\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee B$
and by Lemma 10, we reach
$\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee B$
and by Lemma 10, we reach
![]() $\bigwedge \Gamma \wedge (\bigvee \Delta \vee A) \rhd _{\alpha } (\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A)$
. Therefore,
$\bigwedge \Gamma \wedge (\bigvee \Delta \vee A) \rhd _{\alpha } (\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A)$
. Therefore,
![]() $\bigwedge \Gamma \rhd _{\alpha } (\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A)$
, by part
$\bigwedge \Gamma \rhd _{\alpha } (\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A)$
, by part
![]() $(i)$
in Lemma 11. Finally, as
$(i)$
in Lemma 11. Finally, as
![]() $(\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A) \to \bigvee \Delta \vee (A \wedge B)$
is provable in
$(\bigvee \Delta \vee B) \wedge (\bigvee \Delta \vee A) \to \bigvee \Delta \vee (A \wedge B)$
is provable in
![]() $\textrm{PV}$
, by Lemmas 10 and 11, we reach
$\textrm{PV}$
, by Lemmas 10 and 11, we reach
![]() $\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee (A \wedge B)$
. The proof for
$\bigwedge \Gamma \rhd _{\alpha } \bigvee \Delta \vee (A \wedge B)$
. The proof for
![]() $(iv)$
is similar.
$(iv)$
is similar.
Having the required lemmas, we are now ready to prove the following theorem as the main extraction technique that witnesses the proofs in
![]() $\textrm{TI}(\forall _1, \prec )$
by
$\textrm{TI}(\forall _1, \prec )$
by
![]() $\alpha$
-flows.
$\alpha$
-flows.
Theorem.
Let
![]() $\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
. Then,
$\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
. Then,
![]() $\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
$\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
![]() $\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
.
$\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
.
Proof.
We first prove the easier direction. Assume
![]() $\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
and the pair
$\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
and the pair
![]() $(H(\gamma, \bar{x}), \beta )$
is an
$(H(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $\bigwedge \Gamma (\bar{x})$
to
$\bigwedge \Gamma (\bar{x})$
to
![]() $\bigvee \Delta (\bar{x})$
. As
$\bigvee \Delta (\bar{x})$
. As
![]() $\textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
and
$\textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
and
![]() $\textrm{TI}(\forall _1, \prec )$
extends
$\textrm{TI}(\forall _1, \prec )$
extends
![]() $\textrm{PV}$
, we have
$\textrm{PV}$
, we have
Then, as
![]() $H(\gamma, \bar{x}) \in \forall _1$
, by the transfinite induction in
$H(\gamma, \bar{x}) \in \forall _1$
, by the transfinite induction in
![]() $\textrm{TI}(\forall _1, \prec )$
, we reach
$\textrm{TI}(\forall _1, \prec )$
, we reach
![]() $\textrm{TI}(\forall _1, \prec ) \vdash H(0, \bar{x}) \rightarrow H(\beta, \bar{x})$
. Finally, using the
$\textrm{TI}(\forall _1, \prec ) \vdash H(0, \bar{x}) \rightarrow H(\beta, \bar{x})$
. Finally, using the
![]() $\textrm{PV}$
-provable equivalences
$\textrm{PV}$
-provable equivalences
![]() $\bigwedge \Gamma (\bar{x}) \leftrightarrow H(0, \bar{x})$
and
$\bigwedge \Gamma (\bar{x}) \leftrightarrow H(0, \bar{x})$
and
![]() $H(\beta, \bar{x}) \leftrightarrow \bigvee \Delta (\bar{x})$
, we reach
$H(\beta, \bar{x}) \leftrightarrow \bigvee \Delta (\bar{x})$
, we reach
![]() $\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
.
$\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
.
For the other direction, assume
![]() $\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
. By Lemma 8,
$\textrm{TI}(\forall _1, \prec ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
. By Lemma 8,
![]() $\Gamma (\bar{x}) \Rightarrow \Delta (\bar{x})$
has a
$\Gamma (\bar{x}) \Rightarrow \Delta (\bar{x})$
has a
![]() $\textbf{G}_1$
-proof only consisting of
$\textbf{G}_1$
-proof only consisting of
![]() $\forall _1$
-formulas. By induction on this proof, we show that for any sequent
$\forall _1$
-formulas. By induction on this proof, we show that for any sequent
![]() $\Sigma \Rightarrow \Lambda$
in the proof, we have
$\Sigma \Rightarrow \Lambda$
in the proof, we have
![]() $\Sigma \rhd _{\alpha } \Lambda$
.
$\Sigma \rhd _{\alpha } \Lambda$
.
For the axioms, as they are provable in
![]() $\textrm{PV}$
, using Lemma 10, there is nothing to prove. The case of structural rules (except for the weak cut) is easy. Weak cut and weak induction are addressed in Lemma 11. The conjunction and disjunction rules are proved in Lemma 12. For the right universal quantifier rule, if
$\textrm{PV}$
, using Lemma 10, there is nothing to prove. The case of structural rules (except for the weak cut) is easy. Weak cut and weak induction are addressed in Lemma 11. The conjunction and disjunction rules are proved in Lemma 12. For the right universal quantifier rule, if
![]() $\Sigma (\bar{x}) \Rightarrow \Lambda (\bar{x}), \forall z B(\bar{x}, z)$
is proved from
$\Sigma (\bar{x}) \Rightarrow \Lambda (\bar{x}), \forall z B(\bar{x}, z)$
is proved from
![]() $\Sigma (\bar{x}) \Rightarrow \Lambda (\bar{x}), B(\bar{x}, z)$
, then by induction hypothesis,
$\Sigma (\bar{x}) \Rightarrow \Lambda (\bar{x}), B(\bar{x}, z)$
, then by induction hypothesis,
![]() $\Sigma (\bar{x}) \rhd _{\alpha } \Lambda (\bar{x}), B(\bar{x}, z)$
. Therefore, there exists an
$\Sigma (\bar{x}) \rhd _{\alpha } \Lambda (\bar{x}), B(\bar{x}, z)$
. Therefore, there exists an
![]() $\alpha$
-flow
$\alpha$
-flow
![]() $(H(\gamma, \bar{x}, z), \beta )$
from
$(H(\gamma, \bar{x}, z), \beta )$
from
![]() $\bigwedge \Sigma (\bar{x})$
to
$\bigwedge \Sigma (\bar{x})$
to
![]() $B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})$
. Define
$B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})$
. Define
![]() $I(\gamma, \bar{x})=\forall z H(\gamma, \bar{x}, z)$
and note that
$I(\gamma, \bar{x})=\forall z H(\gamma, \bar{x}, z)$
and note that
![]() $I(\bar{x}, z) \in \forall _1$
. It is easy to see that
$I(\bar{x}, z) \in \forall _1$
. It is easy to see that
![]() $(I(\gamma, \bar{x}), \beta )$
is an
$(I(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $\forall z [\bigwedge \Sigma (\bar{x})]$
to
$\forall z [\bigwedge \Sigma (\bar{x})]$
to
![]() $\forall z [B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})]$
, as
$\forall z [B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})]$
, as
![]() $\textrm{PV}$
-provability of
$\textrm{PV}$
-provability of
![]() $\forall \gamma \prec \delta H(\gamma, z, \bar{x}) \rightarrow H(\delta, z, \bar{x})$
implies the
$\forall \gamma \prec \delta H(\gamma, z, \bar{x}) \rightarrow H(\delta, z, \bar{x})$
implies the
![]() $\textrm{PV}$
-provability of
$\textrm{PV}$
-provability of
![]() $\forall \gamma \prec \delta \forall z H(\gamma, z, \bar{x}) \rightarrow \forall z H(\delta, z, \bar{x})$
. Finally, as
$\forall \gamma \prec \delta \forall z H(\gamma, z, \bar{x}) \rightarrow \forall z H(\delta, z, \bar{x})$
. Finally, as
![]() $z$
does not occur as a free variable in
$z$
does not occur as a free variable in
![]() $\Sigma (\bar{x}) \cup \Lambda (\bar{x})$
, we have the
$\Sigma (\bar{x}) \cup \Lambda (\bar{x})$
, we have the
![]() $\textrm{PV}$
-equivalence between
$\textrm{PV}$
-equivalence between
![]() $\forall z [\bigwedge \Sigma (\bar{x})]$
and
$\forall z [\bigwedge \Sigma (\bar{x})]$
and
![]() $\bigwedge \Sigma (\bar{x})$
and similarly between
$\bigwedge \Sigma (\bar{x})$
and similarly between
![]() $\forall z [B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})]$
and
$\forall z [B(\bar{x}, z) \vee \bigvee \Lambda (\bar{x})]$
and
![]() $\bigvee \Lambda (\bar{x}) \vee \forall z B(\bar{x}, z)$
. Using Lemmas 10 and 11, we can prove
$\bigvee \Lambda (\bar{x}) \vee \forall z B(\bar{x}, z)$
. Using Lemmas 10 and 11, we can prove
![]() $\bigwedge \Sigma (\bar{x}) \rhd _{\alpha } \bigvee \Lambda (\bar{x}) \vee \forall z B(\bar{x}, z)$
. For the left universal quantifier rule, if
$\bigwedge \Sigma (\bar{x}) \rhd _{\alpha } \bigvee \Lambda (\bar{x}) \vee \forall z B(\bar{x}, z)$
. For the left universal quantifier rule, if
![]() $\Sigma (\bar{x}), \forall z B(\bar{x}, z) \Rightarrow \Lambda (\bar{x})$
is proved from
$\Sigma (\bar{x}), \forall z B(\bar{x}, z) \Rightarrow \Lambda (\bar{x})$
is proved from
![]() $\Sigma (\bar{x}), B(\bar{x}, s(\bar{x})) \Rightarrow \Lambda (\bar{x})$
, then by induction hypothesis
$\Sigma (\bar{x}), B(\bar{x}, s(\bar{x})) \Rightarrow \Lambda (\bar{x})$
, then by induction hypothesis
![]() $ \Sigma (\bar{x}), B(\bar{x}, s(\bar{x})) \rhd _{\alpha } \Lambda (\bar{x})$
. Since
$ \Sigma (\bar{x}), B(\bar{x}, s(\bar{x})) \rhd _{\alpha } \Lambda (\bar{x})$
. Since
![]() $\textrm{PV} \vdash \bigwedge \Sigma (\bar{x}) \wedge \forall z B(\bar{x}, z) \rightarrow \bigwedge \Sigma (\bar{x}) \wedge B(\bar{x}, s(\bar{x}))$
, by Lemmas 10 and 11, we reach
$\textrm{PV} \vdash \bigwedge \Sigma (\bar{x}) \wedge \forall z B(\bar{x}, z) \rightarrow \bigwedge \Sigma (\bar{x}) \wedge B(\bar{x}, s(\bar{x}))$
, by Lemmas 10 and 11, we reach
![]() $\Sigma (\bar{x}), \forall z B(\bar{x}, z) \rhd _{\alpha } \Lambda (\bar{x})$
.
$\Sigma (\bar{x}), \forall z B(\bar{x}, z) \rhd _{\alpha } \Lambda (\bar{x})$
.
Corollary 13.
Let
![]() $\alpha$
be an ordinal with the ptime representation
$\alpha$
be an ordinal with the ptime representation
![]() $\mathfrak{O}$
. Then,
$\mathfrak{O}$
. Then,
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}(\prec _\beta ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}(\prec _\beta ) \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
![]() $\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
, for
$\Gamma (\bar{x}) \rhd _{\alpha } \Delta (\bar{x})$
, for
![]() $\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
.
$\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
.
Proof.
As any implication in the form
![]() $\bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
is logically equivalent to a
$\bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
is logically equivalent to a
![]() $\Pi ^0_2$
-formula, the claim is a consequence of Theorem 4 and Corollary 7.
$\Pi ^0_2$
-formula, the claim is a consequence of Theorem 4 and Corollary 7.
Corollary 14.
Let
![]() $\mathfrak{O}_{0}$
be the ptime representation for
$\mathfrak{O}_{0}$
be the ptime representation for
![]() $\varepsilon _0$
introduced in Subsection
3.1
. Then,
$\varepsilon _0$
introduced in Subsection
3.1
. Then,
![]() $\textrm{PA} \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
$\textrm{PA} \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
![]() $\Gamma (\bar{x}) \rhd _{\varepsilon _0} \Delta (\bar{x})$
, for
$\Gamma (\bar{x}) \rhd _{\varepsilon _0} \Delta (\bar{x})$
, for
![]() $\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
.
$\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \forall _1$
.
4.3 Ordinal local search programs
In this subsection, we will first introduce the notion of an ordinal local search program as a formalized version of the transfinite ptime modifications over an initial ptime value that we explained before. We will then use these programs to witness some provable statements in the theory
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
.
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
.
Definition 15.
Let
![]() $T$
be a theory over the language
$T$
be a theory over the language
![]() $\mathcal{L}_{\textrm{PV}}$
. A total search problem of
$\mathcal{L}_{\textrm{PV}}$
. A total search problem of
![]() $T$
is a quantifier-free formula
$T$
is a quantifier-free formula
![]() $A(\bar{x}, \bar{y})$
such that
$A(\bar{x}, \bar{y})$
such that
![]() $T \vdash \forall \bar{x} \exists \bar{y} A(\bar{x}, \bar{y})$
. A total search problem is called an
$T \vdash \forall \bar{x} \exists \bar{y} A(\bar{x}, \bar{y})$
. A total search problem is called an
![]() $\textrm{NP}$
-search problem, if there are sequences of polynomials
$\textrm{NP}$
-search problem, if there are sequences of polynomials
![]() $\bar{r}$
such that
$\bar{r}$
such that
![]() $\textrm{PV} \vdash A(\bar{x}, \bar{y}) \to |\bar{y}| \leq \bar{r}(|\bar{x}|)$
, where
$\textrm{PV} \vdash A(\bar{x}, \bar{y}) \to |\bar{y}| \leq \bar{r}(|\bar{x}|)$
, where
![]() $|\bar{y}| \leq \bar{r}(|\bar{x}|)$
is an abbreviation for
$|\bar{y}| \leq \bar{r}(|\bar{x}|)$
is an abbreviation for
![]() $\bigwedge _i (|y_i| \leq r_i(|\bar{x}|))$
. We denote the class of all these total search (resp.,
$\bigwedge _i (|y_i| \leq r_i(|\bar{x}|))$
. We denote the class of all these total search (resp.,
![]() $\textrm{NP}$
-search) problems of
$\textrm{NP}$
-search) problems of
![]() $T$
by
$T$
by
![]() $\textrm{TSP}(T)$
(resp.
$\textrm{TSP}(T)$
(resp.
![]() $\textrm{TFNP}(T)$
).
$\textrm{TFNP}(T)$
).
Definition 16.
Let
![]() $\alpha$
be an ordinal,
$\alpha$
be an ordinal,
![]() $\mathfrak{O}$
be its ptime representation,
$\mathfrak{O}$
be its ptime representation,
![]() $A(\bar{x}, \bar{y})$
be a quantifier-free formula in
$A(\bar{x}, \bar{y})$
be a quantifier-free formula in
![]() $\mathcal{L}_{\textrm{PV}}$
and
$\mathcal{L}_{\textrm{PV}}$
and
![]() $\beta \in \mathcal{O}$
. By an
$\beta \in \mathcal{O}$
. By an
![]() $\textrm{LS}(\preceq _{\beta })$
-program for
$\textrm{LS}(\preceq _{\beta })$
-program for
![]() $A(\bar{x}, \bar{y})$
, we mean the following data: an initial sequence of
$A(\bar{x}, \bar{y})$
, we mean the following data: an initial sequence of
![]() $\mathcal{L}_{\textrm{PV}}$
-terms
$\mathcal{L}_{\textrm{PV}}$
-terms
![]() $\bar{i}(\bar{x})$
, a quantifier-free
$\bar{i}(\bar{x})$
, a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}}$
-formula
$\mathcal{L}_{\textrm{PV}}$
-formula
![]() $G(\gamma, \bar{x}, \bar{z})$
, a sequence of
$G(\gamma, \bar{x}, \bar{z})$
, a sequence of
![]() $\mathcal{L}_{\textrm{PV}}$
-terms
$\mathcal{L}_{\textrm{PV}}$
-terms
![]() $\bar{N}(\gamma, \bar{x}, \bar{z})$
, an
$\bar{N}(\gamma, \bar{x}, \bar{z})$
, an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $q(\gamma, \bar{x}, \bar{z})$
, a sequence of
$q(\gamma, \bar{x}, \bar{z})$
, a sequence of
![]() $\mathcal{L}_{\textrm{PV}}$
-terms
$\mathcal{L}_{\textrm{PV}}$
-terms
![]() $\bar{p}(\bar{x}, \bar{z})$
, such that:
$\bar{p}(\bar{x}, \bar{z})$
, such that:
-
•
 $\textrm{PV} \vdash G(\beta, \bar{x}, \bar{i}(\bar{x}))$
,
$\textrm{PV} \vdash G(\beta, \bar{x}, \bar{i}(\bar{x}))$
, -
•
 $\textrm{PV} \vdash \gamma \neq 0 \to q(\gamma, \bar{x}, \bar{z}) \prec \gamma$
,
$\textrm{PV} \vdash \gamma \neq 0 \to q(\gamma, \bar{x}, \bar{z}) \prec \gamma$
, -
•
 $\textrm{PV} \vdash \gamma \neq 0 \to [G(\gamma, \bar{x}, \bar{z}) \to G(q(\gamma, \bar{x}, \bar{z}), \bar{x}, \bar{N}(\gamma, \bar{x}, \bar{z}))]$
,
$\textrm{PV} \vdash \gamma \neq 0 \to [G(\gamma, \bar{x}, \bar{z}) \to G(q(\gamma, \bar{x}, \bar{z}), \bar{x}, \bar{N}(\gamma, \bar{x}, \bar{z}))]$
, -
•
 $\textrm{PV} \vdash G(0, \bar{x}, \bar{z}) \to A(\bar{x}, \bar{p}(\bar{x}, \bar{z}))$
.
$\textrm{PV} \vdash G(0, \bar{x}, \bar{z}) \to A(\bar{x}, \bar{p}(\bar{x}, \bar{z}))$
.
By
![]() $\textrm{LS}(\preceq _{\beta })$
, we mean the class of all formulas
$\textrm{LS}(\preceq _{\beta })$
, we mean the class of all formulas
![]() $A(\bar{x}, \bar{y})$
for which there exists a
$A(\bar{x}, \bar{y})$
for which there exists a
![]() $\textrm{LS}(\preceq _{\beta })$
-program. By
$\textrm{LS}(\preceq _{\beta })$
-program. By
![]() $\textrm{PLS}(\preceq _{\beta })$
, we mean the class
$\textrm{PLS}(\preceq _{\beta })$
, we mean the class
![]() $\textrm{LS}(\preceq _{\beta }) \cap \textrm{TFNP}(Th(\mathbb{N}))$
.
$\textrm{LS}(\preceq _{\beta }) \cap \textrm{TFNP}(Th(\mathbb{N}))$
.
Membership
![]() $A(\bar{x}, \bar{y}) \in \textrm{LS}(\preceq _{\beta })$
implies
$A(\bar{x}, \bar{y}) \in \textrm{LS}(\preceq _{\beta })$
implies
![]() $\forall \bar{x} \exists \bar{y}A(\bar{x}, \bar{y})$
and the
$\forall \bar{x} \exists \bar{y}A(\bar{x}, \bar{y})$
and the
![]() $\textrm{LS}(\preceq _{\beta })$
-program actually provides an algorithm to compute
$\textrm{LS}(\preceq _{\beta })$
-program actually provides an algorithm to compute
![]() $\bar{y}$
from
$\bar{y}$
from
![]() $\bar{x}$
. To see this, denote
$\bar{x}$
. To see this, denote
![]() $G(\gamma, \bar{x}, \bar{z})$
by
$G(\gamma, \bar{x}, \bar{z})$
by
![]() $G_{\gamma }$
. The algorithm starts at the level
$G_{\gamma }$
. The algorithm starts at the level
![]() $\beta$
with an initial value
$\beta$
with an initial value
![]() $\bar{i}(\bar{x})$
satisfying the property
$\bar{i}(\bar{x})$
satisfying the property
![]() $G_{\beta }$
. Then, using the feasible function
$G_{\beta }$
. Then, using the feasible function
![]() $q$
, it finds a lower level to go to and uses the modification
$q$
, it finds a lower level to go to and uses the modification
![]() $\bar{N}$
to update any value with the property
$\bar{N}$
to update any value with the property
![]() $G_{\gamma }$
to a value satisfying the property
$G_{\gamma }$
to a value satisfying the property
![]() $G_{q(\gamma )}$
. Finally, reaching the zeroth level, the algorithm uses
$G_{q(\gamma )}$
. Finally, reaching the zeroth level, the algorithm uses
![]() $\bar{p}$
to compute
$\bar{p}$
to compute
![]() $\bar{y}$
satisfying
$\bar{y}$
satisfying
![]() $A$
from any value with the property
$A$
from any value with the property
![]() $G_0$
.
$G_0$
.
The next theorem uses
![]() $\textrm{LS}(\preceq _{\beta })$
-programs (
$\textrm{LS}(\preceq _{\beta })$
-programs (
![]() $\textrm{PLS}(\preceq _{\beta })$
-programs) to witness the total search (
$\textrm{PLS}(\preceq _{\beta })$
-programs) to witness the total search (
![]() $\textrm{NP}$
-search) problems of
$\textrm{NP}$
-search) problems of
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
. The idea is using Herbrand’s theorem, Theorem 2, applied on
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}})$
. The idea is using Herbrand’s theorem, Theorem 2, applied on
![]() $\textrm{PV}$
to push the data extraction of Corollary 13 a bit further to reach an ordinal local search program for total search problems.
$\textrm{PV}$
to push the data extraction of Corollary 13 a bit further to reach an ordinal local search program for total search problems.
Theorem.
Let
![]() $\alpha$
be an ordinal with the ptime representation
$\alpha$
be an ordinal with the ptime representation
![]() $\mathfrak{O}$
. Then
$\mathfrak{O}$
. Then
![]() $\textrm{TSP}(\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}))= \bigcup _{\beta \in \mathcal{O}} \textrm{LS}(\preceq _{\beta })$
and
$\textrm{TSP}(\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}))= \bigcup _{\beta \in \mathcal{O}} \textrm{LS}(\preceq _{\beta })$
and
![]() $\textrm{TFNP}(\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}))= \bigcup _{\beta \in \mathcal{O}} \textrm{PLS}(\preceq _{\beta })$
.
$\textrm{TFNP}(\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}))= \bigcup _{\beta \in \mathcal{O}} \textrm{PLS}(\preceq _{\beta })$
.
Proof.
We only prove the first equality. The second is just a consequence. For the first direction, assume that
![]() $A(\bar{x}, \bar{y})$
has a
$A(\bar{x}, \bar{y})$
has a
![]() $\textrm{LS}(\preceq _{\beta })$
-program. Set
$\textrm{LS}(\preceq _{\beta })$
-program. Set
![]() $H(\gamma, \bar{x})=\forall \bar{z} \neg G(\gamma, \bar{x}, \bar{z}) \wedge \forall \bar{y} \neg A(\bar{x}, \bar{y})$
and note that
$H(\gamma, \bar{x})=\forall \bar{z} \neg G(\gamma, \bar{x}, \bar{z}) \wedge \forall \bar{y} \neg A(\bar{x}, \bar{y})$
and note that
![]() $H \in \forall _1$
. We claim that
$H \in \forall _1$
. We claim that
![]() $(H(\gamma, \bar{x}), \beta )$
is an
$(H(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $\forall \bar{y} \neg A(\bar{x}, \bar{y})$
to
$\forall \bar{y} \neg A(\bar{x}, \bar{y})$
to
![]() $\bot$
. First, as
$\bot$
. First, as
![]() $\textrm{PV} \vdash G(0, \bar{x}, \bar{z}) \to A(\bar{x}, \bar{p}(\bar{x}, \bar{z}))$
, we have
$\textrm{PV} \vdash G(0, \bar{x}, \bar{z}) \to A(\bar{x}, \bar{p}(\bar{x}, \bar{z}))$
, we have
![]() $\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \forall \bar{z} \neg G(0, \bar{x}, \bar{z})$
and hence
$\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \forall \bar{z} \neg G(0, \bar{x}, \bar{z})$
and hence
![]() $\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \leftrightarrow H(0, \bar{x})$
. Second, as
$\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \leftrightarrow H(0, \bar{x})$
. Second, as
![]() $\textrm{PV} \vdash G(\beta, \bar{x}, \bar{i}(\bar{x}))$
, we reach
$\textrm{PV} \vdash G(\beta, \bar{x}, \bar{i}(\bar{x}))$
, we reach
![]() $\textrm{PV} \vdash \forall \bar{z} \neg G(\beta, \bar{x}, \bar{z}) \leftrightarrow \bot$
and hence
$\textrm{PV} \vdash \forall \bar{z} \neg G(\beta, \bar{x}, \bar{z}) \leftrightarrow \bot$
and hence
![]() $\textrm{PV} \vdash \bot \leftrightarrow H(\beta, \bar{x})$
. Finally, using
$\textrm{PV} \vdash \bot \leftrightarrow H(\beta, \bar{x})$
. Finally, using
![]() $\textrm{PV} \vdash \gamma \neq 0 \to q(\gamma, \bar{x}, \bar{z}) \prec \gamma$
, and
$\textrm{PV} \vdash \gamma \neq 0 \to q(\gamma, \bar{x}, \bar{z}) \prec \gamma$
, and
it is easy to see that
and hence we reach
The latter implies
![]() $ \textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
. Therefore,
$ \textrm{PV} \vdash \forall \; 1 \preceq \delta \preceq \beta \; [\forall \gamma \prec \delta \; H(\gamma, \bar{x}) \rightarrow H(\delta, \bar{x})]$
. Therefore,
![]() $(H(\gamma, \bar{x}), \beta )$
is an
$(H(\gamma, \bar{x}), \beta )$
is an
![]() $\alpha$
-flow from
$\alpha$
-flow from
![]() $\forall \bar{y} \neg A(\bar{x}, \bar{y})$
to
$\forall \bar{y} \neg A(\bar{x}, \bar{y})$
to
![]() $\bot$
. Hence,
$\bot$
. Hence,
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \bot$
, by Corollary 13 and thus, we reach
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \bot$
, by Corollary 13 and thus, we reach
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{x} \exists \bar{y} \, A(\bar{x}, \bar{y})$
. For the converse, assume that
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{x} \exists \bar{y} \, A(\bar{x}, \bar{y})$
. For the converse, assume that
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{x} \exists \bar{y} A(\bar{x}, \bar{y})$
, where
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{x} \exists \bar{y} A(\bar{x}, \bar{y})$
, where
![]() $A(\bar{x}, \bar{y}) \in \mathcal{L}_{\textrm{PV}}$
is quantifier-free. As
$A(\bar{x}, \bar{y}) \in \mathcal{L}_{\textrm{PV}}$
is quantifier-free. As
![]() $\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \bot$
, by Corollary 13,
$\textrm{PA}+\bigcup _{\beta \in \mathcal{O}}\textrm{TI}({\prec_{\beta}}) \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \to \bot$
, by Corollary 13,
![]() $\forall \bar{y} \neg A(\bar{x}, \bar{y}) \rhd _{\alpha } \bot$
. Hence, there exist
$\forall \bar{y} \neg A(\bar{x}, \bar{y}) \rhd _{\alpha } \bot$
. Hence, there exist
![]() $H(\gamma, \bar{x}) \in \forall _1$
and
$H(\gamma, \bar{x}) \in \forall _1$
and
![]() $\beta \in \mathcal{O}$
such that
$\beta \in \mathcal{O}$
such that
![]() $\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \leftrightarrow H(0, \bar{x})$
,
$\textrm{PV} \vdash \forall \bar{y} \neg A(\bar{x}, \bar{y}) \leftrightarrow H(0, \bar{x})$
,
![]() $\textrm{PV} \vdash H(\beta, \bar{x}) \leftrightarrow \bot$
and
$\textrm{PV} \vdash H(\beta, \bar{x}) \leftrightarrow \bot$
and
As
![]() $H \in \forall _1$
, there exists a quantifier-free formula
$H \in \forall _1$
, there exists a quantifier-free formula
![]() $I(\gamma, \bar{x}, \bar{z})$
such that
$I(\gamma, \bar{x}, \bar{z})$
such that
![]() $H(\gamma, \bar{x})$
and
$H(\gamma, \bar{x})$
and
![]() $\forall \bar{z} I(\gamma, \bar{x}, \bar{z})$
are equivalent over
$\forall \bar{z} I(\gamma, \bar{x}, \bar{z})$
are equivalent over
![]() $\textrm{PV}$
. On the other hand, as the implications are provable in
$\textrm{PV}$
. On the other hand, as the implications are provable in
![]() $\textrm{PV}$
, we can witness the existential quantifiers by ptime functions. Hence, there are
$\textrm{PV}$
, we can witness the existential quantifiers by ptime functions. Hence, there are
![]() $\mathcal{L}_{\textrm{PV}}$
-terms
$\mathcal{L}_{\textrm{PV}}$
-terms
![]() $\bar{Y}(\bar{x}, \bar{z})$
,
$\bar{Y}(\bar{x}, \bar{z})$
,
![]() $\bar{Z}(\gamma, \bar{x}, \bar{z})$
,
$\bar{Z}(\gamma, \bar{x}, \bar{z})$
,
![]() $\Delta (\gamma, \bar{x}, \bar{z})$
, and
$\Delta (\gamma, \bar{x}, \bar{z})$
, and
![]() $\bar{W}(\bar{x})$
such that
$\bar{W}(\bar{x})$
such that
-
•
 $\textrm{PV} \vdash \neg A(\bar{x}, \bar{Y}(\bar{x}, \bar{z})) \rightarrow I(0, \bar{x}, \bar{z})$
,
$\textrm{PV} \vdash \neg A(\bar{x}, \bar{Y}(\bar{x}, \bar{z})) \rightarrow I(0, \bar{x}, \bar{z})$
, -
•
 $\textrm{PV} \vdash I(\beta, \bar{x}, \bar{W}(\bar{x})) \rightarrow \bot$
,
$\textrm{PV} \vdash I(\beta, \bar{x}, \bar{W}(\bar{x})) \rightarrow \bot$
, -
•
 $\textrm{PV} \vdash \forall 1 \preceq \delta \preceq \beta \; [[(\Delta (\delta, \bar{x}, \bar{z}) \prec \delta \rightarrow I(\Delta (\delta, \bar{x}, \bar{z}), \bar{x}, \bar{Z}(\delta, \bar{x}, \bar{z}))] \rightarrow I(\delta, \bar{x}, \bar{z})]$
.
$\textrm{PV} \vdash \forall 1 \preceq \delta \preceq \beta \; [[(\Delta (\delta, \bar{x}, \bar{z}) \prec \delta \rightarrow I(\Delta (\delta, \bar{x}, \bar{z}), \bar{x}, \bar{Z}(\delta, \bar{x}, \bar{z}))] \rightarrow I(\delta, \bar{x}, \bar{z})]$
.
Define
![]() $G(\delta, \bar{x}, \bar{z})=\neg I(\delta, \bar{x}, \bar{z}) \wedge (\delta \preceq \beta )$
,
$G(\delta, \bar{x}, \bar{z})=\neg I(\delta, \bar{x}, \bar{z}) \wedge (\delta \preceq \beta )$
,
 \begin{equation*} q(\delta, \bar {x}, \bar {z})= \begin {cases} \Delta (\delta, \bar {x}, \bar {z}) & \neg I(\delta, \bar {x}, \bar {z}) \wedge (\delta \preceq \beta ) \\ 0 & \text {otherwise} \end {cases} \end{equation*}
\begin{equation*} q(\delta, \bar {x}, \bar {z})= \begin {cases} \Delta (\delta, \bar {x}, \bar {z}) & \neg I(\delta, \bar {x}, \bar {z}) \wedge (\delta \preceq \beta ) \\ 0 & \text {otherwise} \end {cases} \end{equation*}
![]() $\bar{i}(\bar{x})= \bar{W}(\bar{x})$
and
$\bar{i}(\bar{x})= \bar{W}(\bar{x})$
and
![]() $\bar{p}(\bar{x}, \bar{z})=\bar{Y}(\bar{x}, \bar{z})$
. It is easy to see that this new data is an
$\bar{p}(\bar{x}, \bar{z})=\bar{Y}(\bar{x}, \bar{z})$
. It is easy to see that this new data is an
![]() $\textrm{LS}(\preceq _{\beta })$
-program for
$\textrm{LS}(\preceq _{\beta })$
-program for
![]() $A(\bar{x}, \bar{y})$
.
$A(\bar{x}, \bar{y})$
.
Applying Theorem 5 to
![]() $\alpha =\varepsilon _0$
, we reach the following Corollary, originally proved in Beckmann (Reference Beckmann2009).
$\alpha =\varepsilon _0$
, we reach the following Corollary, originally proved in Beckmann (Reference Beckmann2009).
Corollary 17.
Let
![]() $\mathfrak{O}_{0}$
be the ptime representation of the ordinal
$\mathfrak{O}_{0}$
be the ptime representation of the ordinal
![]() $\varepsilon _0$
introduced in Subsection
3.1
. Then
$\varepsilon _0$
introduced in Subsection
3.1
. Then
![]() $\textrm{TSP}(\textrm{PA})= \bigcup _{\beta \in \mathcal{O}_{0}} \textrm{LS}(\preceq _{\beta })$
and
$\textrm{TSP}(\textrm{PA})= \bigcup _{\beta \in \mathcal{O}_{0}} \textrm{LS}(\preceq _{\beta })$
and
![]() $\textrm{TFNP}(\textrm{PA})= \bigcup _{\beta \in \mathcal{O}_{0}} \textrm{PLS}(\preceq _{\beta })$
.
$\textrm{TFNP}(\textrm{PA})= \bigcup _{\beta \in \mathcal{O}_{0}} \textrm{PLS}(\preceq _{\beta })$
.
5.
 $k$
-Flows and Bounded Arithmetic
$k$
-Flows and Bounded Arithmetic
In this section, we will modify the method developed for the strong theories of arithmetic in Section 4 to also cover the bounded and hence weaker theories of arithmetic. The structure of the present section is similar to that of Section 4. After recalling the usual sequent calculi for the theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
in Subsection 5.1, the next subsection, Subsection 5.2 will be devoted to investigate a suitable version of a flow for bounded arithmetic called a
$T^k_2$
in Subsection 5.1, the next subsection, Subsection 5.2 will be devoted to investigate a suitable version of a flow for bounded arithmetic called a
![]() $k$
-flow. Roughly speaking, a
$k$
-flow. Roughly speaking, a
![]() $k$
-flow is an exponentially long uniform sequence of
$k$
-flow is an exponentially long uniform sequence of
![]() $\textrm{PV}$
-provable implications between
$\textrm{PV}$
-provable implications between
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas in the class
$\mathcal{L}_{\textrm{PV}}$
-formulas in the class
![]() $\hat{\Pi }^b_k$
. After proving some basic properties of
$\hat{\Pi }^b_k$
. After proving some basic properties of
![]() $k$
-flows, we will conclude the subsection by proving a witnessing theorem, transforming the proofs of the implications between
$k$
-flows, we will conclude the subsection by proving a witnessing theorem, transforming the proofs of the implications between
![]() $\hat{\Pi }^b_k$
-formulas in
$\hat{\Pi }^b_k$
-formulas in
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
to some types of
$T^k_2$
to some types of
![]() $k$
-flows. Finally, in Subsection 5.3, we will introduce the appropriate notion of a local search program to witness the
$k$
-flows. Finally, in Subsection 5.3, we will introduce the appropriate notion of a local search program to witness the
![]() $\textrm{PV}$
-provable implications further and find a complete witnessing for the theories
$\textrm{PV}$
-provable implications further and find a complete witnessing for the theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
.
$T^k_2$
.
5.1 Sequent calculi for bounded arithmetic
To recall the usual sequent calculi for
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
, introduced in Buss (Reference Buss1986), first consider the following rules:
$T^k_2$
, introduced in Buss (Reference Buss1986), first consider the following rules:
Bounded Quantifier Rules:
Induction Rules:
In the rules
![]() $(R\forall ^{\leq })$
and
$(R\forall ^{\leq })$
and
![]() $(L\exists ^{\leq })$
as well as in the induction rules, the variable
$(L\exists ^{\leq })$
as well as in the induction rules, the variable
![]() $z$
should not appear in the consequence of the rule. Moreover, in the induction rules
$z$
should not appear in the consequence of the rule. Moreover, in the induction rules
![]() $(\textrm{PInd}_k)$
and
$(\textrm{PInd}_k)$
and
![]() $(\textrm{Ind}_k)$
, the index
$(\textrm{Ind}_k)$
, the index
![]() $k$
means that the formula
$k$
means that the formula
![]() $A(z)$
is restricted to the class
$A(z)$
is restricted to the class
![]() $\hat{\Pi }^b_k$
.
$\hat{\Pi }^b_k$
.
The system
![]() $\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) for
$\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) for
![]() $S^k_2$
(resp.
$S^k_2$
(resp.
![]() $T^k_2$
) is defined as the system
$T^k_2$
) is defined as the system
![]() $\textbf{LPV}$
plus the bounded quantifier rules and the rule
$\textbf{LPV}$
plus the bounded quantifier rules and the rule
![]() $(\textrm{PInd}_k)$
(resp.
$(\textrm{PInd}_k)$
(resp.
![]() $(\textrm{Ind}_k)$
). For some technical reasons, we prefer to work with the alternative systems where the cut and the induction rules are weakened. Define the system
$(\textrm{Ind}_k)$
). For some technical reasons, we prefer to work with the alternative systems where the cut and the induction rules are weakened. Define the system
![]() $\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) similar to
$\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) similar to
![]() $\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) with the difference that in the former the quantifier rules in
$\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) with the difference that in the former the quantifier rules in
![]() $\textbf{LPV}$
are omitted and the cut and the induction rule
$\textbf{LPV}$
are omitted and the cut and the induction rule
![]() $(\textrm{PInd}_k)$
(resp.
$(\textrm{PInd}_k)$
(resp.
![]() $(\textrm{Ind}_k)$
) are replaced by the weak cut and the weak induction rule
$(\textrm{Ind}_k)$
) are replaced by the weak cut and the weak induction rule
![]() $(\textrm{wPInd}_k)$
(resp.
$(\textrm{wPInd}_k)$
(resp.
![]() $(\textrm{wInd}_k)$
) depicted below:
$(\textrm{wInd}_k)$
) depicted below:
In the weak induction rules, we have the similar constraints as before, namely that
![]() $A \in \hat{\Pi }^b_k$
and
$A \in \hat{\Pi }^b_k$
and
![]() $z$
does not appear in the consequence of the rules. Note that the only point modified in the weak induction rules is the missing context
$z$
does not appear in the consequence of the rules. Note that the only point modified in the weak induction rules is the missing context
![]() $\Delta$
.
$\Delta$
.
The following theorem ensures that the system
![]() $\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) is complete for the sequents of
$\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) is complete for the sequents of
![]() $\hat{\Pi }^b_k$
-formulas. Notice that the lemma does not claim the full completeness as the system
$\hat{\Pi }^b_k$
-formulas. Notice that the lemma does not claim the full completeness as the system
![]() $\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) is clearly weak to introduce any unbounded quantifier.
$\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
) is clearly weak to introduce any unbounded quantifier.
Lemma 18.
For any
![]() $\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
:
$\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
:
-
• If
 $S^k_2 \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
$S^k_2 \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
 $\Gamma \Rightarrow \Delta$
has a
$\Gamma \Rightarrow \Delta$
has a
 $\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
$\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
 $\hat{\Pi }^b_k$
-formulas.
$\hat{\Pi }^b_k$
-formulas.
-
• If
 $T^k_2 \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
$T^k_2 \vdash \bigwedge \Gamma \rightarrow \bigvee \Delta$
, then
 $\Gamma \Rightarrow \Delta$
has a
$\Gamma \Rightarrow \Delta$
has a
 $\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
$\textbf{wLT}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
 $\hat{\Pi }^b_k$
-formulas.
$\hat{\Pi }^b_k$
-formulas.
Proof.
It is a well-known consequence of the cut reduction theorem for
![]() $\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) that if
$\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) that if
![]() $\bigwedge \Gamma \to \bigvee \Delta$
is provable in
$\bigwedge \Gamma \to \bigvee \Delta$
is provable in
![]() $S^k_2$
(resp.
$S^k_2$
(resp.
![]() $T^k_2$
), it has a proof in
$T^k_2$
), it has a proof in
![]() $\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
$\textbf{LS}^{\textbf{k}}_{\textbf{2}}$
(resp.
![]() $\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) only consisting of
$\textbf{LT}^{\textbf{k}}_{\textbf{2}}$
) only consisting of
![]() $\hat{\Pi }^b_k$
-formulas and only using bounded quantifier rules instead of the usual unbounded quantifier rules in
$\hat{\Pi }^b_k$
-formulas and only using bounded quantifier rules instead of the usual unbounded quantifier rules in
![]() $\textbf{LPV}$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Therefore, the only thing remained to prove is simulating the cut and the induction rules over
$\textbf{LPV}$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Therefore, the only thing remained to prove is simulating the cut and the induction rules over
![]() $\hat{\Pi }^b_k$
-formulas by their weak versions applied over the same family of formulas. This simulation is almost identical to the one presented in the proof of Lemma 8 and hence will be skipped here.
$\hat{\Pi }^b_k$
-formulas by their weak versions applied over the same family of formulas. This simulation is almost identical to the one presented in the proof of Lemma 8 and hence will be skipped here.
5.2
 $k$
-flows
$k$
-flows
In this subsection, we will first introduce a
![]() $k$
-flow as a uniform term-length sequence of
$k$
-flow as a uniform term-length sequence of
![]() $\textrm{PV}$
-provable implications between
$\textrm{PV}$
-provable implications between
![]() $\hat{\Pi }^b_k$
-formulas. Then, we will develop a high-level calculus for
$\hat{\Pi }^b_k$
-formulas. Then, we will develop a high-level calculus for
![]() $k$
-flows to witness the provability in theories
$k$
-flows to witness the provability in theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
.
$T^k_2$
.
Definition 19.
Let
![]() $A(\bar{x}), B(\bar{x}) \in \hat{\Pi }^b_k$
be two
$A(\bar{x}), B(\bar{x}) \in \hat{\Pi }^b_k$
be two
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas and
$\mathcal{L}_{\textrm{PV}}$
-formulas and
![]() $t(\bar{x})$
be an
$t(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-term. A
$\mathcal{L}_{\textrm{PV}}$
-term. A
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
with the length
$B(\bar{x})$
with the length
![]() $t(\bar{x})$
is a pair
$t(\bar{x})$
is a pair
![]() $(H(u, \bar{x}), t(\bar{x}))$
, where
$(H(u, \bar{x}), t(\bar{x}))$
, where
![]() $H(u, \bar{x}) \in \hat{\Pi }^b_k$
and:
$H(u, \bar{x}) \in \hat{\Pi }^b_k$
and:
-
•
 $\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow A(\bar{x})$
.
$\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow A(\bar{x})$
. -
•
 $\textrm{PV} \vdash H(t(\bar{x}), \bar{x}) \leftrightarrow B(\bar{x})$
.
$\textrm{PV} \vdash H(t(\bar{x}), \bar{x}) \leftrightarrow B(\bar{x})$
. -
•
 $\textrm{PV} \vdash \forall u \lt t(\bar{x}) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
$\textrm{PV} \vdash \forall u \lt t(\bar{x}) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
A
![]() $k$
-flow is called polynomial if
$k$
-flow is called polynomial if
![]() $t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
$t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
![]() $q$
, where by equality, we mean the syntactical equality between the terms. If there exists a
$q$
, where by equality, we mean the syntactical equality between the terms. If there exists a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
with the length
$B(\bar{x})$
with the length
![]() $t(\bar{x})$
, we write
$t(\bar{x})$
, we write
![]() $A(\bar{x}) \rhd ^{t(\bar{x})}_{k} B(\bar{x})$
. If we intend to emphasize on the existence of the
$A(\bar{x}) \rhd ^{t(\bar{x})}_{k} B(\bar{x})$
. If we intend to emphasize on the existence of the
![]() $k$
-flow regardless of its length, we write
$k$
-flow regardless of its length, we write
![]() $A(\bar{x}) \rhd _k B(\bar{x})$
and if the
$A(\bar{x}) \rhd _k B(\bar{x})$
and if the
![]() $k$
-flow is polynomial
$k$
-flow is polynomial
![]() $A(\bar{x}) \rhd ^p_{k} B(\bar{x})$
. Moreover, if
$A(\bar{x}) \rhd ^p_{k} B(\bar{x})$
. Moreover, if
![]() $\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
, by
$\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
, by
![]() $\Gamma \rhd _k \Delta$
(resp.
$\Gamma \rhd _k \Delta$
(resp.
![]() $\Gamma \rhd ^p_k \Delta$
), we mean
$\Gamma \rhd ^p_k \Delta$
), we mean
![]() $\bigwedge \Gamma \rhd _k \bigvee \Delta$
(resp.
$\bigwedge \Gamma \rhd _k \bigvee \Delta$
(resp.
![]() $\bigwedge \Gamma \rhd ^p_k \bigvee \Delta$
).
$\bigwedge \Gamma \rhd ^p_k \bigvee \Delta$
).
Similar to the situation with the ordinal flows, it is also reasonable to provide a high-level calculus to work with the
![]() $k$
-flows. The following series of lemmas realize this goal.
$k$
-flows. The following series of lemmas realize this goal.
Lemma 20.
(Padding) Let
![]() $A(\bar{x}), B(\bar{x}) \in \hat{\Pi }^b_k$
and
$A(\bar{x}), B(\bar{x}) \in \hat{\Pi }^b_k$
and
![]() $t(\bar{x}), s(\bar{x})$
be two
$t(\bar{x}), s(\bar{x})$
be two
![]() $\mathcal{L}_{\textrm{PV}}$
-terms such that
$\mathcal{L}_{\textrm{PV}}$
-terms such that
![]() $\textrm{PV} \vdash t(\bar{x}) \leq s(\bar{x})$
. If
$\textrm{PV} \vdash t(\bar{x}) \leq s(\bar{x})$
. If
![]() $A(\bar{x}) \rhd _k^{t(\bar{x})} B(\bar{x})$
, then
$A(\bar{x}) \rhd _k^{t(\bar{x})} B(\bar{x})$
, then
![]() $A(\bar{x}) \rhd _k^{s(\bar{x})} B(\bar{x})$
. Therefore, without loss of generality, we can always assume that the length
$A(\bar{x}) \rhd _k^{s(\bar{x})} B(\bar{x})$
. Therefore, without loss of generality, we can always assume that the length
![]() $t(\bar{x})$
of a
$t(\bar{x})$
of a
![]() $k$
-flow is
$k$
-flow is
![]() $\textrm{PV}$
-monotone, that is,
$\textrm{PV}$
-monotone, that is,
![]() $\textrm{PV} \vdash \bigwedge _{i=1}^n (x_i \leq y_i) \to t(\bar{x}) \leq t(\bar{y})$
.
$\textrm{PV} \vdash \bigwedge _{i=1}^n (x_i \leq y_i) \to t(\bar{x}) \leq t(\bar{y})$
.
Proof.
Let
![]() $(H(u, \bar{x}),t(\bar{x}))$
be a
$(H(u, \bar{x}),t(\bar{x}))$
be a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
. Then, define
$B(\bar{x})$
. Then, define
 \begin{equation*} H'(u, \bar {x})= \begin {cases} H(u, \bar {x}) & u \leq t(\bar {x})\\ B(\bar {x}) & u \gt t(\bar {x}) \end {cases} \end{equation*}
\begin{equation*} H'(u, \bar {x})= \begin {cases} H(u, \bar {x}) & u \leq t(\bar {x})\\ B(\bar {x}) & u \gt t(\bar {x}) \end {cases} \end{equation*}
Notice that
![]() $H'(u, \bar{x}) \in \hat{\Pi }^b_k$
. It is easy to prove that
$H'(u, \bar{x}) \in \hat{\Pi }^b_k$
. It is easy to prove that
![]() $(H'(u, \bar{x}), s(\bar{x}))$
is a
$(H'(u, \bar{x}), s(\bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
. The only thing worth emphasizing is the role of the assumption
$B(\bar{x})$
. The only thing worth emphasizing is the role of the assumption
![]() $\textrm{PV} \vdash t(\bar{x}) \leq s(\bar{x})$
in the proof. This assumption together with the definition of
$\textrm{PV} \vdash t(\bar{x}) \leq s(\bar{x})$
in the proof. This assumption together with the definition of
![]() $H'(u, \bar{x})$
shows
$H'(u, \bar{x})$
shows
![]() $\textrm{PV} \vdash H'(s(\bar{x}), \bar{x}) \leftrightarrow B(\bar{x})$
which is one of the conditions of being a
$\textrm{PV} \vdash H'(s(\bar{x}), \bar{x}) \leftrightarrow B(\bar{x})$
which is one of the conditions of being a
![]() $k$
-flow. This observation completes the proof of the first part of the claim. For its second part, note that for any term
$k$
-flow. This observation completes the proof of the first part of the claim. For its second part, note that for any term
![]() $t(\bar{x})$
, there exists a polynomial
$t(\bar{x})$
, there exists a polynomial
![]() $q$
such that
$q$
such that
![]() $\textrm{PV} \vdash t(\bar{x}) \leq 2^{q(|\bar{x}|)}$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). As
$\textrm{PV} \vdash t(\bar{x}) \leq 2^{q(|\bar{x}|)}$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). As
![]() $2^{q(|\bar{x}|)}$
is
$2^{q(|\bar{x}|)}$
is
![]() $\textrm{PV}$
-monotone, it is enough to use the first part to extend a
$\textrm{PV}$
-monotone, it is enough to use the first part to extend a
![]() $k$
-flow with the length
$k$
-flow with the length
![]() $t(\bar{x})$
to a
$t(\bar{x})$
to a
![]() $k$
-flow with the length
$k$
-flow with the length
![]() $2^{q(|\bar{x}|)}$
. For polynomial
$2^{q(|\bar{x}|)}$
. For polynomial
![]() $k$
-flows, as the length
$k$
-flows, as the length
![]() $t(\bar{x})$
is in the form
$t(\bar{x})$
is in the form
![]() $q(|\bar{x}|)$
, for some polynomial
$q(|\bar{x}|)$
, for some polynomial
![]() $q$
, it is already
$q$
, it is already
![]() $\textrm{PV}$
-monotone and hence there is nothing to prove.
$\textrm{PV}$
-monotone and hence there is nothing to prove.
Lemma 21.
Let
![]() $A(\bar{x}), B(\bar{x}), C(\bar{x}) \in \hat{\Pi }^b_k$
. Then:
$A(\bar{x}), B(\bar{x}), C(\bar{x}) \in \hat{\Pi }^b_k$
. Then:
-
(i) If
 $\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, then
$\textrm{PV} \vdash A(\bar{x}) \to B(\bar{x})$
, then
 $A(\bar{x}) \rhd ^p_k B(\bar{x})$
.
$A(\bar{x}) \rhd ^p_k B(\bar{x})$
. -
(ii) If
 $A(\bar{x}) \rhd _k B(\bar{x})$
, then
$A(\bar{x}) \rhd _k B(\bar{x})$
, then
 $A(\bar{x}) \circ C(\bar{x}) \rhd _k B(\bar{x}) \circ C(\bar{x})$
, for any
$A(\bar{x}) \circ C(\bar{x}) \rhd _k B(\bar{x}) \circ C(\bar{x})$
, for any
 $\circ \in \{\wedge, \vee \}$
. A similar claim also holds for
$\circ \in \{\wedge, \vee \}$
. A similar claim also holds for
 $\rhd ^p_k$
.
$\rhd ^p_k$
.
Proof. The proof is similar to that of Lemma 10.
Lemma 22.
(Bounded variables) Let
![]() $A(\bar{x}, y), B(\bar{x}, y) \in \hat{\Pi }^b_k$
be two
$A(\bar{x}, y), B(\bar{x}, y) \in \hat{\Pi }^b_k$
be two
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas and
$\mathcal{L}_{\textrm{PV}}$
-formulas and
![]() $s(\bar{x})$
be an
$s(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-term (not depending on
$\mathcal{L}_{\textrm{PV}}$
-term (not depending on
![]() $y$
). If
$y$
). If
![]() $A(\bar{x}, y) \rhd _k B(\bar{x}, y)$
, then there exists a formula
$A(\bar{x}, y) \rhd _k B(\bar{x}, y)$
, then there exists a formula
![]() $I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
and an
$I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
and an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $r(\bar{x})$
(not depending on
$r(\bar{x})$
(not depending on
![]() $y$
) such that:
$y$
) such that:
-
•
 $\textrm{PV} \vdash I(0, y, \bar{x}) \leftrightarrow A(\bar{x}, y)$
.
$\textrm{PV} \vdash I(0, y, \bar{x}) \leftrightarrow A(\bar{x}, y)$
. -
•
 $\textrm{PV} \vdash \forall y \leq s(\bar{x}) [I(r(\bar{x}), y, \bar{x}) \leftrightarrow B(\bar{x}, y)]$
.
$\textrm{PV} \vdash \forall y \leq s(\bar{x}) [I(r(\bar{x}), y, \bar{x}) \leftrightarrow B(\bar{x}, y)]$
. -
•
 $\textrm{PV} \vdash I(u, y, \bar{x}) \rightarrow I(u+1, y, \bar{x})$
.
$\textrm{PV} \vdash I(u, y, \bar{x}) \rightarrow I(u+1, y, \bar{x})$
. -
•
 $\textrm{PV} \vdash r(\bar{x}) \geq 1$
.
$\textrm{PV} \vdash r(\bar{x}) \geq 1$
.
If we also have
![]() $A(\bar{x}, y) \rhd ^p_k B(\bar{x}, y)$
, then the term
$A(\bar{x}, y) \rhd ^p_k B(\bar{x}, y)$
, then the term
![]() $r(\bar{x})$
can be chosen in the form
$r(\bar{x})$
can be chosen in the form
![]() $q(|\bar{x}|)$
, for some polynomial
$q(|\bar{x}|)$
, for some polynomial
![]() $q$
.
$q$
.
Proof.
Assume
![]() $(H(u, y, \bar{x}), t(y, \bar{x}))$
is a
$(H(u, y, \bar{x}), t(y, \bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x}, y)$
to
$A(\bar{x}, y)$
to
![]() $B(\bar{x}, y)$
. Using Lemma 20, we can assume that
$B(\bar{x}, y)$
. Using Lemma 20, we can assume that
![]() $t(y, \bar{x})$
is
$t(y, \bar{x})$
is
![]() $\textrm{PV}$
-monotone and
$\textrm{PV}$
-monotone and
![]() $\textrm{PV} \vdash t(y, \bar{x}) \geq 1$
. Define
$\textrm{PV} \vdash t(y, \bar{x}) \geq 1$
. Define
 \begin{equation*} I(u, y, \bar {x})= \begin {cases} H(u, y, \bar {x}) & u \leq t(y, \bar {x})\\ B(y, \bar {x}) & u \gt t(y,\bar {x}) \end {cases} \end{equation*}
\begin{equation*} I(u, y, \bar {x})= \begin {cases} H(u, y, \bar {x}) & u \leq t(y, \bar {x})\\ B(y, \bar {x}) & u \gt t(y,\bar {x}) \end {cases} \end{equation*}
and notice that
![]() $I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
. Recall from the basic facts in bounded arithmetic that for the term
$I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
. Recall from the basic facts in bounded arithmetic that for the term
![]() $s(\bar{x})$
, there is a polynomial
$s(\bar{x})$
, there is a polynomial
![]() $q_s$
such that
$q_s$
such that
![]() $\textrm{PV} \vdash |s(\bar{x})| \leq q_s(|\bar{x}|)$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Define
$\textrm{PV} \vdash |s(\bar{x})| \leq q_s(|\bar{x}|)$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Define
![]() $r(\bar{x})=t(2^{q_s(|\bar{x}|)}, \bar{x})$
and note that
$r(\bar{x})=t(2^{q_s(|\bar{x}|)}, \bar{x})$
and note that
![]() $\textrm{PV} \vdash y \leq s(\bar{x}) \to t(y, \bar{x}) \leq r(\bar{x})$
, as
$\textrm{PV} \vdash y \leq s(\bar{x}) \to t(y, \bar{x}) \leq r(\bar{x})$
, as
![]() $t(y, \bar{x})$
is
$t(y, \bar{x})$
is
![]() $\textrm{PV}$
-monotone and
$\textrm{PV}$
-monotone and
![]() $\textrm{PV} \vdash r(\bar{x}) \geq 1$
. We claim that
$\textrm{PV} \vdash r(\bar{x}) \geq 1$
. We claim that
![]() $I(u, y, \bar{x})$
and
$I(u, y, \bar{x})$
and
![]() $r(\bar{x})$
work. The first and the third claims in the statement of the lemma are the trivial consequences of the fact that
$r(\bar{x})$
work. The first and the third claims in the statement of the lemma are the trivial consequences of the fact that
![]() $(H(u, y, \bar{x}), t(y, \bar{x}))$
is a
$(H(u, y, \bar{x}), t(y, \bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x}, y)$
to
$A(\bar{x}, y)$
to
![]() $B(\bar{x}, y)$
. For the second, notice that as
$B(\bar{x}, y)$
. For the second, notice that as
![]() $\textrm{PV} \vdash y \leq s(\bar{x}) \to t(y, \bar{x}) \leq r(\bar{x})$
, we can use the definition of
$\textrm{PV} \vdash y \leq s(\bar{x}) \to t(y, \bar{x}) \leq r(\bar{x})$
, we can use the definition of
![]() $I(y, \bar{x})$
to see that the formula
$I(y, \bar{x})$
to see that the formula
![]() $I(r(\bar{x}), \bar{x})$
is
$I(r(\bar{x}), \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(y, \bar{x})$
.
$B(y, \bar{x})$
.
For the polynomial case, if
![]() $(H(u, y, \bar{x}), t(y, \bar{x}))$
is a polynomial
$(H(u, y, \bar{x}), t(y, \bar{x}))$
is a polynomial
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x}, y)$
to
$A(\bar{x}, y)$
to
![]() $B(\bar{x}, y)$
, then there is a polynomial
$B(\bar{x}, y)$
, then there is a polynomial
![]() $q_t$
such that
$q_t$
such that
![]() $t(y, \bar{x})=q_t(|y|, |\bar{x}|)$
. Therefore,
$t(y, \bar{x})=q_t(|y|, |\bar{x}|)$
. Therefore,
![]() $r(\bar{x})=q_t(q_s(|x|)+1, |\bar{x}|)$
which implies that
$r(\bar{x})=q_t(q_s(|x|)+1, |\bar{x}|)$
which implies that
![]() $r(\bar{x})$
is in the form
$r(\bar{x})$
is in the form
![]() $q_r(|\bar{x}|)$
, for some poynomial
$q_r(|\bar{x}|)$
, for some poynomial
![]() $q_r$
.
$q_r$
.
Lemma 23.
Let
![]() $\Gamma (\bar{x}) \cup \{A(\bar{x}), B(\bar{x}), C(\bar{x}), D(y, \bar{x})\} \subseteq \hat{\Pi }^b_k$
. Then:
$\Gamma (\bar{x}) \cup \{A(\bar{x}), B(\bar{x}), C(\bar{x}), D(y, \bar{x})\} \subseteq \hat{\Pi }^b_k$
. Then:
-
(i) (weak gluing) If
 $A(\bar{x}) \rhd _k B(\bar{x})$
and
$A(\bar{x}) \rhd _k B(\bar{x})$
and
 $ B(\bar{x}) \rhd _k C(\bar{x})$
then
$ B(\bar{x}) \rhd _k C(\bar{x})$
then
 $A(\bar{x}) \rhd _k C(\bar{x})$
. A similar claim also holds for
$A(\bar{x}) \rhd _k C(\bar{x})$
. A similar claim also holds for
 $\rhd ^p_k$
.
$\rhd ^p_k$
. -
(ii) (polynomial strong gluing) If
 $\Gamma (\bar{x}), D(\lfloor \frac{y}{2}\rfloor, \bar{x}) \rhd ^p_k D(y, \bar{x})$
, then we have
$\Gamma (\bar{x}), D(\lfloor \frac{y}{2}\rfloor, \bar{x}) \rhd ^p_k D(y, \bar{x})$
, then we have
 $\Gamma (\bar{x}), D(0, \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
, for any
$\Gamma (\bar{x}), D(0, \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
, for any
 $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
 $s(\bar{x})$
.
$s(\bar{x})$
. -
(iii) (strong gluing) If
 $ \Gamma (\bar{x}), D(y, \bar{x}) \rhd _k D(y+1, \bar{x})$
, then
$ \Gamma (\bar{x}), D(y, \bar{x}) \rhd _k D(y+1, \bar{x})$
, then
 $\Gamma (\bar{x}), D(0, \bar{x}) \rhd _k D(s(\bar{x}), \bar{x})$
, for any
$\Gamma (\bar{x}), D(0, \bar{x}) \rhd _k D(s(\bar{x}), \bar{x})$
, for any
 $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
 $s(\bar{x})$
.
$s(\bar{x})$
.
Proof.
For
![]() $(i)$
, as
$(i)$
, as
![]() $A(\bar{x}) \rhd _k B(\bar{x})$
and
$A(\bar{x}) \rhd _k B(\bar{x})$
and
![]() $ B(\bar{x}) \rhd _k C(\bar{x})$
, there exist
$ B(\bar{x}) \rhd _k C(\bar{x})$
, there exist
![]() $k$
-flows
$k$
-flows
![]() $(H(u, \bar{x}), t(\bar{x}))$
and
$(H(u, \bar{x}), t(\bar{x}))$
and
![]() $(H'(u, \bar{x}), t'(\bar{x}))$
, from
$(H'(u, \bar{x}), t'(\bar{x}))$
, from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $B(\bar{x})$
and from
$B(\bar{x})$
and from
![]() $B(\bar{x})$
to
$B(\bar{x})$
to
![]() $C(\bar{x})$
, respectively. Set
$C(\bar{x})$
, respectively. Set
![]() $t''(\bar{x})=t(\bar{x})+t'(\bar{x})+1$
and
$t''(\bar{x})=t(\bar{x})+t'(\bar{x})+1$
and
 \begin{equation*} H''(u, \bar {x})= \begin {cases} H(u, \bar {x}) & u \leq t(\bar {x})\\ H'(u \dot {-} (t(\bar {x}) + 1), \bar {x}) & u \gt t(\bar {x}) \end {cases} \end{equation*}
\begin{equation*} H''(u, \bar {x})= \begin {cases} H(u, \bar {x}) & u \leq t(\bar {x})\\ H'(u \dot {-} (t(\bar {x}) + 1), \bar {x}) & u \gt t(\bar {x}) \end {cases} \end{equation*}
Notice that
![]() $H''(u, \bar{x})$
is clearly a
$H''(u, \bar{x})$
is clearly a
![]() $\hat{\Pi }^b_k$
-formula. We claim that
$\hat{\Pi }^b_k$
-formula. We claim that
![]() $(H''(u, \bar{x}), t''(\bar{x}))$
is a
$(H''(u, \bar{x}), t''(\bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $C(\bar{x})$
as depicted in the following figure (for simplicity, in the figure, we sometimes drop the free variables
$C(\bar{x})$
as depicted in the following figure (for simplicity, in the figure, we sometimes drop the free variables
![]() $\bar{x}$
):
$\bar{x}$
):

First, it is trivial that
![]() $H''(0, \bar{x})$
is
$H''(0, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(0, \bar{x})$
which is
$H(0, \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $A(\bar{x})$
. Similarly,
$A(\bar{x})$
. Similarly,
![]() $H''(t''(\bar{x}), \bar{x})$
is
$H''(t''(\bar{x}), \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H'(t'(\bar{x}), \bar{x})$
which is
$H'(t'(\bar{x}), \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $C(\bar{x})$
. To prove
$C(\bar{x})$
. To prove
![]() $\textrm{PV} \vdash \forall u \lt t''(\bar{x}) \; [H''(u, \bar{x}) \to H''(u+1, \bar{x})]$
, the cases
$\textrm{PV} \vdash \forall u \lt t''(\bar{x}) \; [H''(u, \bar{x}) \to H''(u+1, \bar{x})]$
, the cases
![]() $u \lt t(\bar{x})$
and
$u \lt t(\bar{x})$
and
![]() $t(\bar{x}) \lt u \lt t''(\bar{x})$
are reduced to a similar claim for
$t(\bar{x}) \lt u \lt t''(\bar{x})$
are reduced to a similar claim for
![]() $H$
and
$H$
and
![]() $H'$
. For
$H'$
. For
![]() $u=t(\bar{x})$
, note that
$u=t(\bar{x})$
, note that
![]() $H''(t(\bar{x}), \bar{x})$
is
$H''(t(\bar{x}), \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H(t(\bar{x}), \bar{x})$
and
$H(t(\bar{x}), \bar{x})$
and
![]() $H''(t(\bar{x})+1, \bar{x})$
is
$H''(t(\bar{x})+1, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H'(0, \bar{x})$
. As both formulas are
$H'(0, \bar{x})$
. As both formulas are
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $B(\bar{x})$
, the proof is complete. Finally, note that if the
$B(\bar{x})$
, the proof is complete. Finally, note that if the
![]() $k$
-flows
$k$
-flows
![]() $(H(u, \bar{x}), t(\bar{x}))$
and
$(H(u, \bar{x}), t(\bar{x}))$
and
![]() $(H'(u, \bar{x}), t'(\bar{x}))$
are polynomial, there are polynomials
$(H'(u, \bar{x}), t'(\bar{x}))$
are polynomial, there are polynomials
![]() $q$
and
$q$
and
![]() $q'$
such that
$q'$
such that
![]() $t(\bar{x})=q(|\bar{x}|)$
and
$t(\bar{x})=q(|\bar{x}|)$
and
![]() $t'(\bar{x})=q'(|\bar{x}|)$
. Hence,
$t'(\bar{x})=q'(|\bar{x}|)$
. Hence,
![]() $t''(\bar{x})=q(|\bar{x}|)+q'(|\bar{x}|)+1$
. Therefore, the
$t''(\bar{x})=q(|\bar{x}|)+q'(|\bar{x}|)+1$
. Therefore, the
![]() $k$
-flow
$k$
-flow
![]() $(H''(u, \bar{x}), t''(\bar{x}))$
is also polynomial.
$(H''(u, \bar{x}), t''(\bar{x}))$
is also polynomial.
For
![]() $(ii)$
, as
$(ii)$
, as
![]() $\Gamma (\bar{x}), D(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k D(y, \bar{x})$
, by Lemma 21, we have
$\Gamma (\bar{x}), D(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k D(y, \bar{x})$
, by Lemma 21, we have
![]() $\bigwedge \Gamma (\bar{x}) \wedge D(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k \bigwedge \Gamma \wedge D(y, \bar{x})$
. For simplicity, denote
$\bigwedge \Gamma (\bar{x}) \wedge D(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k \bigwedge \Gamma \wedge D(y, \bar{x})$
. For simplicity, denote
![]() $\bigwedge \Gamma (\bar{x}) \wedge D(y, \bar{x})$
by
$\bigwedge \Gamma (\bar{x}) \wedge D(y, \bar{x})$
by
![]() $E(y, \bar{x})$
. Therefore, we have
$E(y, \bar{x})$
. Therefore, we have
![]() $E(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k E(y, \bar{x})$
. First, we want to prove
$E(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k E(y, \bar{x})$
. First, we want to prove
![]() $E(0, \bar{x}) \rhd ^p_k E(s(\bar{x}), \bar{x})$
. Roughly speaking, the idea is gluing the polynomial
$E(0, \bar{x}) \rhd ^p_k E(s(\bar{x}), \bar{x})$
. Roughly speaking, the idea is gluing the polynomial
![]() $k$
-flows from
$k$
-flows from
![]() $E(\lfloor \frac{y}{2} \rfloor, \bar{x})$
to
$E(\lfloor \frac{y}{2} \rfloor, \bar{x})$
to
![]() $E(y, \bar{x})$
, one after another, starting from
$E(y, \bar{x})$
, one after another, starting from
![]() $y=s(\bar{x})$
till reaching
$y=s(\bar{x})$
till reaching
![]() $E(0, \bar{x})$
:
$E(0, \bar{x})$
:

Notice that the result of this gluing extends the length of the
![]() $k$
-flow by
$k$
-flow by
![]() $|s(\bar{x})|$
which is bounded by a polynomial and hence acceptable. More formally, using Lemma 22 for the formulas
$|s(\bar{x})|$
which is bounded by a polynomial and hence acceptable. More formally, using Lemma 22 for the formulas
![]() $E(\lfloor \frac{y}{2} \rfloor, \bar{x})$
and
$E(\lfloor \frac{y}{2} \rfloor, \bar{x})$
and
![]() $E(y, \bar{x})$
and the term
$E(y, \bar{x})$
and the term
![]() $2s(\bar{x})$
(the choice of
$2s(\bar{x})$
(the choice of
![]() $2s(\bar{x})$
instead of
$2s(\bar{x})$
instead of
![]() $s(\bar{x})$
is rather technical) and using the fact that
$s(\bar{x})$
is rather technical) and using the fact that
![]() $E(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k E(y, \bar{x})$
, we reach a pair
$E(\lfloor \frac{y}{2} \rfloor, \bar{x}) \rhd ^p_k E(y, \bar{x})$
, we reach a pair
![]() $(H'(u, y, \bar{x}), t'(\bar{x}))$
such that:
$(H'(u, y, \bar{x}), t'(\bar{x}))$
such that:
-
(1)
 $\textrm{PV} \vdash H'(0, y, \bar{x}) \leftrightarrow E(\lfloor \frac{y}{2} \rfloor,\bar{x})$
,
$\textrm{PV} \vdash H'(0, y, \bar{x}) \leftrightarrow E(\lfloor \frac{y}{2} \rfloor,\bar{x})$
, -
(2)
 $\textrm{PV} \vdash \forall y \leq 2s(\bar{x}) [H'(t'(\bar{x}), y, \bar{x}) \leftrightarrow E(y, \bar{x})]$
,
$\textrm{PV} \vdash \forall y \leq 2s(\bar{x}) [H'(t'(\bar{x}), y, \bar{x}) \leftrightarrow E(y, \bar{x})]$
, -
(3)
 $\textrm{PV} \vdash H'(u, y, \bar{x}) \rightarrow H'(u+1, y, \bar{x})$
,
$\textrm{PV} \vdash H'(u, y, \bar{x}) \rightarrow H'(u+1, y, \bar{x})$
, -
(4)
 $\textrm{PV} \vdash t'(\bar{x}) \geq 1$
,
$\textrm{PV} \vdash t'(\bar{x}) \geq 1$
,
and
![]() $t'(\bar{x})=q_{t'}(|\bar{x}|)$
, for some polynomial
$t'(\bar{x})=q_{t'}(|\bar{x}|)$
, for some polynomial
![]() $q_{t'}$
. Define the function
$q_{t'}$
. Define the function
![]() $Y(z, \bar{x})$
as the result of
$Y(z, \bar{x})$
as the result of
![]() $|s(\bar{x})|+1\dot{-} z$
many iterations of the operation
$|s(\bar{x})|+1\dot{-} z$
many iterations of the operation
![]() $n \mapsto \lfloor \frac{n}{2}\rfloor$
on
$n \mapsto \lfloor \frac{n}{2}\rfloor$
on
![]() $2s(\bar{x})$
. Note that the function is clearly polynomial time computable. Therefore, we can define it recursively in
$2s(\bar{x})$
. Note that the function is clearly polynomial time computable. Therefore, we can define it recursively in
![]() $\textrm{PV}$
and represent it by an
$\textrm{PV}$
and represent it by an
![]() $\mathcal{L}_{\textrm{PV}}$
-term. This term is
$\mathcal{L}_{\textrm{PV}}$
-term. This term is
![]() $\textrm{PV}$
-provably bounded by
$\textrm{PV}$
-provably bounded by
![]() $2s(\bar{x})$
, that is,
$2s(\bar{x})$
, that is,
![]() $\textrm{PV} \vdash Y(z, \bar{x}) \leq 2s(\bar{x})$
and we have
$\textrm{PV} \vdash Y(z, \bar{x}) \leq 2s(\bar{x})$
and we have
![]() $Y(0, \bar{x})=0$
,
$Y(0, \bar{x})=0$
,
![]() $Y(|s(\bar{x})|, \bar{x})=s(\bar{x})$
and if
$Y(|s(\bar{x})|, \bar{x})=s(\bar{x})$
and if
![]() $z \leq |s(\bar{x})|$
, then
$z \leq |s(\bar{x})|$
, then
![]() $Y(z, \bar{x})=\lfloor \frac{Y(z+1, \bar{x})}{2} \rfloor$
, all provable in
$Y(z, \bar{x})=\lfloor \frac{Y(z+1, \bar{x})}{2} \rfloor$
, all provable in
![]() $\textrm{PV}$
. Now, define
$\textrm{PV}$
. Now, define
Note that
![]() $I(u, \bar{x})$
is well defined as
$I(u, \bar{x})$
is well defined as
![]() $t'(\bar{x})$
is greater than zero, provably in
$t'(\bar{x})$
is greater than zero, provably in
![]() $\textrm{PV}$
. It is trivial that
$\textrm{PV}$
. It is trivial that
![]() $I(u, \bar{x}) \in \hat{\Pi }^b_k$
. Set
$I(u, \bar{x}) \in \hat{\Pi }^b_k$
. Set
![]() $r(\bar{x})=t'(\bar{x})|s(\bar{x})|$
. We claim that the pair
$r(\bar{x})=t'(\bar{x})|s(\bar{x})|$
. We claim that the pair
![]() $(I(u, \bar{x}), r(\bar{x}))$
is a
$(I(u, \bar{x}), r(\bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $E(0, \bar{x})$
to
$E(0, \bar{x})$
to
![]() $E(s(\bar{x}),\bar{x})$
as depicted in the following figure. For simplicity, we drop the free variables
$E(s(\bar{x}),\bar{x})$
as depicted in the following figure. For simplicity, we drop the free variables
![]() $\bar{x}$
in the figure.
$\bar{x}$
in the figure.

To prove, we first claim that
The reason is that by definition,
![]() $I(t'(\bar{x})z, \bar{x})=H'(0,Y(z+1, \bar{x}), \bar{x})$
and the latter is
$I(t'(\bar{x})z, \bar{x})=H'(0,Y(z+1, \bar{x}), \bar{x})$
and the latter is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $E(\lfloor \frac{Y(z+1, \bar{x})}{2}\rfloor, \bar{x})$
, by the property
$E(\lfloor \frac{Y(z+1, \bar{x})}{2}\rfloor, \bar{x})$
, by the property
![]() $(1)$
above. Finally, since for any
$(1)$
above. Finally, since for any
![]() $z \leq |s(\bar{x})|$
, we have
$z \leq |s(\bar{x})|$
, we have
![]() $Y(z, \bar{x})=\lfloor \frac{Y(z+1, \bar{x})}{2} \rfloor$
provably in
$Y(z, \bar{x})=\lfloor \frac{Y(z+1, \bar{x})}{2} \rfloor$
provably in
![]() $\textrm{PV}$
, we reach the
$\textrm{PV}$
, we reach the
![]() $\textrm{PV}$
-equivalence with
$\textrm{PV}$
-equivalence with
![]() $E(Y(z, \bar{x}), \bar{x})$
.
$E(Y(z, \bar{x}), \bar{x})$
.
Now, we prove that
![]() $(I(u, \bar{x}), r(\bar{x}))$
is a
$(I(u, \bar{x}), r(\bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $E(0, \bar{x})$
to
$E(0, \bar{x})$
to
![]() $E(s(\bar{x}),\bar{x})$
. First, note that
$E(s(\bar{x}),\bar{x})$
. First, note that
![]() $I(0, \bar{x})$
is
$I(0, \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $E(0, \bar{x})$
, by substituting
$E(0, \bar{x})$
, by substituting
![]() $z=0$
in
$z=0$
in
![]() $(*)$
and using the
$(*)$
and using the
![]() $\textrm{PV}$
-provable fact that
$\textrm{PV}$
-provable fact that
![]() $Y(0, \bar{x})=0$
. Second, note that
$Y(0, \bar{x})=0$
. Second, note that
![]() $I(r(\bar{x}), \bar{x})$
is
$I(r(\bar{x}), \bar{x})$
is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $E(s(\bar{x}), \bar{x})$
, by substituting
$E(s(\bar{x}), \bar{x})$
, by substituting
![]() $z=|s(\bar{x})|$
in
$z=|s(\bar{x})|$
in
![]() $(*)$
and using the
$(*)$
and using the
![]() $\textrm{PV}$
-provable fact that
$\textrm{PV}$
-provable fact that
![]() $Y(|s(\bar{x})|, \bar{x})=s(\bar{x})$
. Third, to prove
$Y(|s(\bar{x})|, \bar{x})=s(\bar{x})$
. Third, to prove
![]() $\textrm{PV} \vdash \forall u \lt t'(\bar{x}) \; [I(u, \bar{x}) \rightarrow I(u+1, \bar{x})]$
, there are two cases to consider: Either
$\textrm{PV} \vdash \forall u \lt t'(\bar{x}) \; [I(u, \bar{x}) \rightarrow I(u+1, \bar{x})]$
, there are two cases to consider: Either
![]() $u+1$
divides
$u+1$
divides
![]() $t'(\bar{x})$
or not. In the latter case, we have
$t'(\bar{x})$
or not. In the latter case, we have
![]() $\lfloor \frac{u+1}{t'(\bar{x})} \rfloor =\lfloor \frac{u}{t'(\bar{x})} \rfloor$
. By definition
$\lfloor \frac{u+1}{t'(\bar{x})} \rfloor =\lfloor \frac{u}{t'(\bar{x})} \rfloor$
. By definition
![]() $I(u, \bar{x})$
is
$I(u, \bar{x})$
is
![]() $H'(u \dot{-} t'(\bar{x})\lfloor \frac{u}{t'(\bar{x})} \rfloor, Y(\lfloor \frac{u}{t'(\bar{x})} \rfloor +1), \bar{x})$
while
$H'(u \dot{-} t'(\bar{x})\lfloor \frac{u}{t'(\bar{x})} \rfloor, Y(\lfloor \frac{u}{t'(\bar{x})} \rfloor +1), \bar{x})$
while
![]() $I(u+1, \bar{x})$
is
$I(u+1, \bar{x})$
is
![]() $H'(u+1 \dot{-} t'(\bar{x})\lfloor \frac{u+1}{t'(\bar{x})} \rfloor, Y(\lfloor \frac{u+1}{t'(\bar{x})} \rfloor +1), \bar{x})$
. Therefore, the former proves the latter by property
$H'(u+1 \dot{-} t'(\bar{x})\lfloor \frac{u+1}{t'(\bar{x})} \rfloor, Y(\lfloor \frac{u+1}{t'(\bar{x})} \rfloor +1), \bar{x})$
. Therefore, the former proves the latter by property
![]() $(3)$
above. For the first case, if
$(3)$
above. For the first case, if
![]() $t'(\bar{x}) | u+1$
, then there exists
$t'(\bar{x}) | u+1$
, then there exists
![]() $z \leq |s(\bar{x})|$
such that
$z \leq |s(\bar{x})|$
such that
![]() $u+1=t'(\bar{x})z$
. Therefore,
$u+1=t'(\bar{x})z$
. Therefore,
![]() $I(u+1, \bar{x})$
is
$I(u+1, \bar{x})$
is
![]() $I(t'(\bar{x})z, \bar{x})$
which is
$I(t'(\bar{x})z, \bar{x})$
which is
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $E(Y(z, \bar{x}), \bar{x})$
by
$E(Y(z, \bar{x}), \bar{x})$
by
![]() $(*)$
, and hence
$(*)$
, and hence
![]() $\textrm{PV}$
-equivalent to
$\textrm{PV}$
-equivalent to
![]() $H'(t'(\bar{x}), Y(z, \bar{x}), \bar{x})$
by
$H'(t'(\bar{x}), Y(z, \bar{x}), \bar{x})$
by
![]() $(2)$
, as
$(2)$
, as
![]() $Y(z, \bar{x})$
is
$Y(z, \bar{x})$
is
![]() $\textrm{PV}$
-provably bounded by
$\textrm{PV}$
-provably bounded by
![]() $2s(\bar{x})$
. As
$2s(\bar{x})$
. As
![]() $I(u, \bar{x})$
is
$I(u, \bar{x})$
is
![]() $H'(t'(\bar{x}) \dot{-} 1, Y(z, \bar{x}), \bar{x})$
by definition, by
$H'(t'(\bar{x}) \dot{-} 1, Y(z, \bar{x}), \bar{x})$
by definition, by
![]() $(3)$
, the formula
$(3)$
, the formula
![]() $I(u, \bar{x})$
implies
$I(u, \bar{x})$
implies
![]() $I(u+1, \bar{x})$
in
$I(u+1, \bar{x})$
in
![]() $\textrm{PV}$
.
$\textrm{PV}$
.
So far, we showed that
![]() $(I(u, \bar{x}), r(\bar{x}))$
is a
$(I(u, \bar{x}), r(\bar{x}))$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $E(0, \bar{x})$
to
$E(0, \bar{x})$
to
![]() $E(s(\bar{x}),\bar{x})$
. Again, recall that for the term
$E(s(\bar{x}),\bar{x})$
. Again, recall that for the term
![]() $s(\bar{x})$
, there is a polynomial
$s(\bar{x})$
, there is a polynomial
![]() $q_s$
such that
$q_s$
such that
![]() $\textrm{PV} \vdash |s(\bar{x})| \leq q_s(|\bar{x}|)$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Hence,
$\textrm{PV} \vdash |s(\bar{x})| \leq q_s(|\bar{x}|)$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995). Hence,
![]() $\textrm{PV} \vdash r(\bar{x}) \leq q_s(|\bar{x}|)q_{t'}(|\bar{x}|)$
. Therefore, using Lemma 20, we can prove the existence of a
$\textrm{PV} \vdash r(\bar{x}) \leq q_s(|\bar{x}|)q_{t'}(|\bar{x}|)$
. Therefore, using Lemma 20, we can prove the existence of a
![]() $k$
-flow with the length
$k$
-flow with the length
![]() $q_s(|\bar{x}|)q_{t'}(|\bar{x}|)$
from
$q_s(|\bar{x}|)q_{t'}(|\bar{x}|)$
from
![]() $E(0, \bar{x})$
to
$E(0, \bar{x})$
to
![]() $E(s(\bar{x}), \bar{x})$
which implies
$E(s(\bar{x}), \bar{x})$
which implies
![]() $E(0, \bar{x}) \rhd ^p_k E(s(\bar{x}), \bar{x})$
. Now, to complete the proof of
$E(0, \bar{x}) \rhd ^p_k E(s(\bar{x}), \bar{x})$
. Now, to complete the proof of
![]() $(ii)$
, by the definition of
$(ii)$
, by the definition of
![]() $E(y, \bar{x})$
, we have
$E(y, \bar{x})$
, we have
![]() $\bigwedge \Gamma (\bar{x}) \wedge D(0, \bar{x}) \rhd ^p_k \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x})$
. As
$\bigwedge \Gamma (\bar{x}) \wedge D(0, \bar{x}) \rhd ^p_k \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x})$
. As
![]() $\textrm{PV} \vdash \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x}) \to D(s(\bar{x}), \bar{x})$
, by Lemma 21, we have
$\textrm{PV} \vdash \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x}) \to D(s(\bar{x}), \bar{x})$
, by Lemma 21, we have
![]() $ \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
. Hence, by the weak gluing, the part
$ \bigwedge \Gamma (\bar{x}) \wedge D(s(\bar{x}), \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
. Hence, by the weak gluing, the part
![]() $(i)$
in the present lemma, we reach
$(i)$
in the present lemma, we reach
![]() $\bigwedge \Gamma (\bar{x}) \wedge D(0, \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
.
$\bigwedge \Gamma (\bar{x}) \wedge D(0, \bar{x}) \rhd ^p_k D(s(\bar{x}), \bar{x})$
.
The proof of
![]() $(iii)$
is similar to that of
$(iii)$
is similar to that of
![]() $(ii)$
and even easier. In this case, one must again define
$(ii)$
and even easier. In this case, one must again define
![]() $E(y, \bar{x})$
as
$E(y, \bar{x})$
as
![]() $\bigwedge \Gamma (\bar{x}) \wedge D(y, \bar{x})$
and then glue the
$\bigwedge \Gamma (\bar{x}) \wedge D(y, \bar{x})$
and then glue the
![]() $k$
-flows from
$k$
-flows from
![]() $E(y, \bar{x})$
to
$E(y, \bar{x})$
to
![]() $E(y+1, \bar{x})$
, one after another, for all
$E(y+1, \bar{x})$
, one after another, for all
![]() $0 \leq y \lt s(\bar{x})$
.
$0 \leq y \lt s(\bar{x})$
.
Lemma 24.
(Conjunction and Disjunction Rules) Let
![]() $\Gamma \cup \Delta \cup \{A, B\} \subseteq \hat{\Pi }^b_k$
. Then:
$\Gamma \cup \Delta \cup \{A, B\} \subseteq \hat{\Pi }^b_k$
. Then:
-
(i) If
 $\Gamma, A \rhd _k \Delta$
or
$\Gamma, A \rhd _k \Delta$
or
 $\Gamma, B \rhd _k \Delta$
then
$\Gamma, B \rhd _k \Delta$
then
 $\Gamma, A \wedge B \rhd _k \Delta$
.
$\Gamma, A \wedge B \rhd _k \Delta$
. -
(ii) If
 $\Gamma \rhd _k A, \Delta$
and
$\Gamma \rhd _k A, \Delta$
and
 $\Gamma \rhd _k B, \Delta$
then
$\Gamma \rhd _k B, \Delta$
then
 $\Gamma \rhd _k A \wedge B, \Delta$
.
$\Gamma \rhd _k A \wedge B, \Delta$
. -
(iii) If
 $\Gamma \rhd _k A, \Delta$
or
$\Gamma \rhd _k A, \Delta$
or
 $\Gamma \rhd _k B, \Delta$
then
$\Gamma \rhd _k B, \Delta$
then
 $\Gamma \rhd _k A \vee B, \Delta$
.
$\Gamma \rhd _k A \vee B, \Delta$
. -
(iv) If
 $\Gamma, A \rhd _k \Delta$
and
$\Gamma, A \rhd _k \Delta$
and
 $\Gamma, B \rhd _k \Delta$
then
$\Gamma, B \rhd _k \Delta$
then
 $\Gamma, A \vee B \rhd _k \Delta$
.
$\Gamma, A \vee B \rhd _k \Delta$
.
A similar claim also holds for
![]() $\rhd ^p_k$
.
$\rhd ^p_k$
.
Proof. The argument is identical to that of Lemma 12 claiming the same fact for the ordinal flows.
Lemma 25.
(Negation Rules) If
![]() $\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
and
$\Gamma \cup \Delta \subseteq \hat{\Pi }^b_k$
and
![]() $A, \neg A \in \hat{\Pi }^b_k$
, then:
$A, \neg A \in \hat{\Pi }^b_k$
, then:
-
(i) If
 $\Gamma, A \rhd _k \Delta$
then
$\Gamma, A \rhd _k \Delta$
then
 $\Gamma \rhd _k \neg A, \Delta$
.
$\Gamma \rhd _k \neg A, \Delta$
. -
(ii) If
 $\Gamma \rhd _k A, \Delta$
then
$\Gamma \rhd _k A, \Delta$
then
 $\Gamma, \neg A \rhd _k \Delta$
.
$\Gamma, \neg A \rhd _k \Delta$
.
A similar claim also holds for
![]() $\rhd ^p_k$
.
$\rhd ^p_k$
.
Proof.
We only prove the claim for
![]() $\rhd _k$
. The case for
$\rhd _k$
. The case for
![]() $\rhd _k^p$
is identical. For
$\rhd _k^p$
is identical. For
![]() $(i)$
, assume
$(i)$
, assume
![]() $\Gamma, A \rhd _k \Delta$
which means
$\Gamma, A \rhd _k \Delta$
which means
![]() $\bigwedge \Gamma \wedge A \rhd _k \bigvee \Delta$
. As
$\bigwedge \Gamma \wedge A \rhd _k \bigvee \Delta$
. As
![]() $\neg A \in \hat{\Pi }^b_k$
, by Lemma 21, we have
$\neg A \in \hat{\Pi }^b_k$
, by Lemma 21, we have
![]() $(\bigwedge \Gamma \wedge A) \vee \neg A \rhd _k \bigvee \Delta \vee \neg A$
. Since
$(\bigwedge \Gamma \wedge A) \vee \neg A \rhd _k \bigvee \Delta \vee \neg A$
. Since
![]() $ \textrm{PV} \vdash \bigwedge \Gamma \rightarrow (\bigwedge \Gamma \wedge A) \vee \neg A$
, by Lemma 21, we have
$ \textrm{PV} \vdash \bigwedge \Gamma \rightarrow (\bigwedge \Gamma \wedge A) \vee \neg A$
, by Lemma 21, we have
![]() $\bigwedge \Gamma \rhd _k (\bigwedge \Gamma \wedge A) \vee \neg A$
. Hence, by weak gluing, Lemma 23, we have
$\bigwedge \Gamma \rhd _k (\bigwedge \Gamma \wedge A) \vee \neg A$
. Hence, by weak gluing, Lemma 23, we have
![]() $\bigwedge \Gamma \rhd _k \bigvee \Delta \vee \neg A$
. The proof for
$\bigwedge \Gamma \rhd _k \bigvee \Delta \vee \neg A$
. The proof for
![]() $(ii)$
is similar.
$(ii)$
is similar.
Lemma 26.
(Bounded Universal Quantifier) Let
![]() $A(\bar{x}), B(\bar{x}, y) \in \hat{\Pi }^b_k$
and
$A(\bar{x}), B(\bar{x}, y) \in \hat{\Pi }^b_k$
and
![]() $s(\bar{x})$
be an
$s(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-term. If
$\mathcal{L}_{\textrm{PV}}$
-term. If
![]() $A(\bar{x}), (y \leq s(\bar{x})) \rhd _k B(\bar{x}, y)$
, then
$A(\bar{x}), (y \leq s(\bar{x})) \rhd _k B(\bar{x}, y)$
, then
![]() $A(\bar{x}) \rhd _k \forall y \leq s(\bar{x}) B(y, \bar{x})$
. The same also holds for
$A(\bar{x}) \rhd _k \forall y \leq s(\bar{x}) B(y, \bar{x})$
. The same also holds for
![]() $\rhd _k^p$
.
$\rhd _k^p$
.
Proof.
Again, we only prove the claim for
![]() $\rhd _k$
. The proof for
$\rhd _k$
. The proof for
![]() $\rhd ^p_k$
is identical. Since
$\rhd ^p_k$
is identical. Since
![]() $A(\bar{x}), (y \leq s(\bar{x})) \rhd _k B(\bar{x}, y)$
and
$A(\bar{x}), (y \leq s(\bar{x})) \rhd _k B(\bar{x}, y)$
and
![]() $y \leq s(\bar{x})$
is quantifier-free, by Lemma 25, we have
$y \leq s(\bar{x})$
is quantifier-free, by Lemma 25, we have
![]() $A(\bar{x}) \rhd _k (y \leq s(\bar{x}) \to B(\bar{x}, y))$
. Note that
$A(\bar{x}) \rhd _k (y \leq s(\bar{x}) \to B(\bar{x}, y))$
. Note that
![]() $(y \leq s(\bar{x}) \to B(\bar{x}, y))$
is defined as
$(y \leq s(\bar{x}) \to B(\bar{x}, y))$
is defined as
![]() $\neg (y \leq s(\bar{x})) \vee B(\bar{x}, y)$
, as the negation is not primitive in the language. Use Lemma 22 for the formulas
$\neg (y \leq s(\bar{x})) \vee B(\bar{x}, y)$
, as the negation is not primitive in the language. Use Lemma 22 for the formulas
![]() $A(\bar{x})$
and
$A(\bar{x})$
and
![]() $(y \leq s(\bar{x}) \to B(\bar{x}, y))$
and the term
$(y \leq s(\bar{x}) \to B(\bar{x}, y))$
and the term
![]() $s(\bar{x})$
. Therefore, we have a formula
$s(\bar{x})$
. Therefore, we have a formula
![]() $I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
and a term
$I(u, y, \bar{x}) \in \hat{\Pi }^b_k$
and a term
![]() $r(\bar{x})$
such that:
$r(\bar{x})$
such that:
-
•
 $\textrm{PV} \vdash I(0, y, \bar{x}) \leftrightarrow A(\bar{x})$
.
$\textrm{PV} \vdash I(0, y, \bar{x}) \leftrightarrow A(\bar{x})$
. -
•
 $\textrm{PV} \vdash \forall y \leq s(\bar{x}) [I(r(\bar{x}), y, \bar{x}) \leftrightarrow (y \leq s(\bar{x}) \to B(\bar{x}, y))]$
.
$\textrm{PV} \vdash \forall y \leq s(\bar{x}) [I(r(\bar{x}), y, \bar{x}) \leftrightarrow (y \leq s(\bar{x}) \to B(\bar{x}, y))]$
. -
•
 $\textrm{PV} \vdash I(u, y, \bar{x}) \rightarrow I(u+1, y, \bar{x})$
.
$\textrm{PV} \vdash I(u, y, \bar{x}) \rightarrow I(u+1, y, \bar{x})$
.
It is easy to see that the pair
![]() $\big (\forall y \leq s(\bar{x}) I(u, y, \bar{x}), r(\bar{x})\big )$
is a
$\big (\forall y \leq s(\bar{x}) I(u, y, \bar{x}), r(\bar{x})\big )$
is a
![]() $k$
-flow from
$k$
-flow from
![]() $A(\bar{x})$
to
$A(\bar{x})$
to
![]() $\forall y \leq s(\bar{x}) B(\bar{x}, y)$
.
$\forall y \leq s(\bar{x}) B(\bar{x}, y)$
.
Now we are ready to use
![]() $k$
-flows to witness the provable implications between
$k$
-flows to witness the provable implications between
![]() $\hat{\Pi }^b_k$
-formulas in
$\hat{\Pi }^b_k$
-formulas in
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
.
$T^k_2$
.
Theorem.
(Soundness and Completeness) Let
![]() $\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \hat{\Pi }^b_k$
. Then:
$\Gamma (\bar{x}) \cup \Delta (\bar{x}) \subseteq \hat{\Pi }^b_k$
. Then:
-
(i)
 $S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
$S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
 $ \Gamma (\bar{x}) \rhd ^p_k \Delta (\bar{x})$
.
$ \Gamma (\bar{x}) \rhd ^p_k \Delta (\bar{x})$
. -
(ii)
 $T^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
$T^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
iff
 $ \Gamma (\bar{x}) \rhd _k \Delta (\bar{x})$
.
$ \Gamma (\bar{x}) \rhd _k \Delta (\bar{x})$
.
Proof.
We only prove
![]() $(i)$
. The proof of
$(i)$
. The proof of
![]() $(ii)$
is similar. First, we prove the easier completeness part. If
$(ii)$
is similar. First, we prove the easier completeness part. If
![]() $\Gamma (\bar{x}) \rhd ^p_{k} \Delta (\bar{x})$
, then by Definition 19, there exist a polynomial
$\Gamma (\bar{x}) \rhd ^p_{k} \Delta (\bar{x})$
, then by Definition 19, there exist a polynomial
![]() $q$
, and a formula
$q$
, and a formula
![]() $H(u, \bar{x}) \in \hat{\Pi }^b_k$
such that:
$H(u, \bar{x}) \in \hat{\Pi }^b_k$
such that:
-
•
 $\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow \bigwedge \Gamma (\bar{x})$
,
$\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow \bigwedge \Gamma (\bar{x})$
, -
•
 $\textrm{PV} \vdash H(q(|\bar{x}|), \bar{x}) \leftrightarrow \bigvee \Delta (\bar{x})$
,
$\textrm{PV} \vdash H(q(|\bar{x}|), \bar{x}) \leftrightarrow \bigvee \Delta (\bar{x})$
, -
•
 $\textrm{PV} \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
$\textrm{PV} \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
Using Lemma 20, without loss of generality, we can also assume that
![]() $\textrm{PV} \vdash q(|\bar{x}|) \geq 1$
. As
$\textrm{PV} \vdash q(|\bar{x}|) \geq 1$
. As
![]() $\textrm{PV}$
is a subtheory of
$\textrm{PV}$
is a subtheory of
![]() $S^k_2$
, we also have all the above provabilities for
$S^k_2$
, we also have all the above provabilities for
![]() $S^k_2$
. Hence,
$S^k_2$
. Hence,
![]() $ S^k_2 \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})].$
Since
$ S^k_2 \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})].$
Since
![]() $H(u, \bar{x}) \in \hat{\Pi }^k_2$
, by the
$H(u, \bar{x}) \in \hat{\Pi }^k_2$
, by the
![]() $\hat{\Pi }^b_k-\textrm{LInd}$
axiom, we have,
$\hat{\Pi }^b_k-\textrm{LInd}$
axiom, we have,
![]() $ S^k_2 \vdash H(0, \bar{x}) \rightarrow H(|2^{q(|\bar{x}|)\dot{-} 1}|, \bar{x})$
. As
$ S^k_2 \vdash H(0, \bar{x}) \rightarrow H(|2^{q(|\bar{x}|)\dot{-} 1}|, \bar{x})$
. As
![]() $\textrm{PV} \vdash q(|\bar{x}|) \geq 1$
, we have
$\textrm{PV} \vdash q(|\bar{x}|) \geq 1$
, we have
![]() $\textrm{PV} \vdash |2^{q(|\bar{x}|)\dot{-} 1}|=|q(\bar{x})|$
. Hence,
$\textrm{PV} \vdash |2^{q(|\bar{x}|)\dot{-} 1}|=|q(\bar{x})|$
. Hence,
![]() $S^k_2 \vdash H(0, \bar{x}) \rightarrow H(q(|\bar{x}|), \bar{x})$
. Therefore,
$S^k_2 \vdash H(0, \bar{x}) \rightarrow H(q(|\bar{x}|), \bar{x})$
. Therefore,
![]() $S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
.
$S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
.
For soundness, assume
![]() $S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
. By Lemma 18,
$S^k_2 \vdash \bigwedge \Gamma (\bar{x}) \rightarrow \bigvee \Delta (\bar{x})$
. By Lemma 18,
![]() $\Gamma (\bar{x}) \Rightarrow \Delta (\bar{x})$
has a
$\Gamma (\bar{x}) \Rightarrow \Delta (\bar{x})$
has a
![]() $\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
$\textbf{wLS}^{\textbf{k}}_{\textbf{2}}$
-proof only consisting of
![]() $\hat{\Pi }^b_k$
-formulas. By induction on this proof, we show that for any sequent
$\hat{\Pi }^b_k$
-formulas. By induction on this proof, we show that for any sequent
![]() $\Sigma \Rightarrow \Lambda$
in the proof, we have
$\Sigma \Rightarrow \Lambda$
in the proof, we have
![]() $\Sigma \rhd ^p_k \Lambda$
. For the axioms, as they are provable in
$\Sigma \rhd ^p_k \Lambda$
. For the axioms, as they are provable in
![]() $\textrm{PV}$
, using Lemma 21, there is nothing to prove. The case of structural rules (except for the weak cut) is easy. Weak cut and
$\textrm{PV}$
, using Lemma 21, there is nothing to prove. The case of structural rules (except for the weak cut) is easy. Weak cut and
![]() $(\textrm{wPInd}_k)$
are addressed in Lemma 23. The conjunction and disjunction rules are proved in Lemma 24 and the rule
$(\textrm{wPInd}_k)$
are addressed in Lemma 23. The conjunction and disjunction rules are proved in Lemma 24 and the rule
![]() $(R\forall ^{\leq })$
is addressed in Lemma 26. Therefore, there are only three cases to consider. If the last rule is
$(R\forall ^{\leq })$
is addressed in Lemma 26. Therefore, there are only three cases to consider. If the last rule is
by the induction hypothesis, we have
![]() $\Sigma (\bar{x}, y), B(\bar{x}, s(\bar{x}, y)) \rhd ^p_k \Lambda (\bar{x}, y)$
. Since
$\Sigma (\bar{x}, y), B(\bar{x}, s(\bar{x}, y)) \rhd ^p_k \Lambda (\bar{x}, y)$
. Since
implies
![]() $\bigwedge \Sigma (\bar{x}, y) \wedge B(\bar{x}, s(\bar{x}, y))$
in
$\bigwedge \Sigma (\bar{x}, y) \wedge B(\bar{x}, s(\bar{x}, y))$
in
![]() $\textrm{PV}$
, by Lemma 21 and weak gluing, Lemma 23, we have
$\textrm{PV}$
, by Lemma 21 and weak gluing, Lemma 23, we have
The case for the rule
![]() $R\exists ^{\leq }$
is similar to the previous case. Finally, if the last rule is
$R\exists ^{\leq }$
is similar to the previous case. Finally, if the last rule is
by the induction hypothesis, we have
![]() $\Sigma (\bar{x}), z \leq s(\bar{x}), B(\bar{x}, z) \rhd ^p_k \Lambda (\bar{x})$
. Since
$\Sigma (\bar{x}), z \leq s(\bar{x}), B(\bar{x}, z) \rhd ^p_k \Lambda (\bar{x})$
. Since
![]() $\exists y \leq s(\bar{x}) B(\bar{x}, y) \in \hat{\Pi }^b_k$
and it starts with an existential quantifier, it must belong to
$\exists y \leq s(\bar{x}) B(\bar{x}, y) \in \hat{\Pi }^b_k$
and it starts with an existential quantifier, it must belong to
![]() $\hat{\Sigma }^b_{k-1}$
. Hence, both
$\hat{\Sigma }^b_{k-1}$
. Hence, both
![]() $\neg B(\bar{x}, z)$
and
$\neg B(\bar{x}, z)$
and
![]() $\neg \exists y \leq s(\bar{x}) B(\bar{x}, y)=\forall y \leq s(\bar{x}) \neg B(\bar{x}, y)$
are in
$\neg \exists y \leq s(\bar{x}) B(\bar{x}, y)=\forall y \leq s(\bar{x}) \neg B(\bar{x}, y)$
are in
![]() $\hat{\Pi }^b_k$
. Therefore, by Lemma 25,
$\hat{\Pi }^b_k$
. Therefore, by Lemma 25,
By using the fact that the names of the parameters are not important in
![]() $k$
-flows and employing Lemma 26, we have
$k$
-flows and employing Lemma 26, we have
![]() $ \Sigma (\bar{x}) \rhd ^p_k \Lambda (\bar{x}), \forall y \leq s(\bar{x}) \; \neg B(\bar{x}, y)$
. Finally again by Lemma 25, we reach
$ \Sigma (\bar{x}) \rhd ^p_k \Lambda (\bar{x}), \forall y \leq s(\bar{x}) \; \neg B(\bar{x}, y)$
. Finally again by Lemma 25, we reach
![]() $ \Sigma (\bar{x}), \exists y \leq s(\bar{x}) B(\bar{x}, y) \rhd ^p_k \Lambda (\bar{x})$
.
$ \Sigma (\bar{x}), \exists y \leq s(\bar{x}) B(\bar{x}, y) \rhd ^p_k \Lambda (\bar{x})$
.
5.3 Reductions and
 $\textrm{PLS}_{(k, l)}$
-programs
$\textrm{PLS}_{(k, l)}$
-programs
In Subsection 5.2, we transformed the
![]() $S^k_2$
-provable (resp.
$S^k_2$
-provable (resp.
![]() $T^k_2$
-provable) implications between
$T^k_2$
-provable) implications between
![]() $\hat{\Pi }^b_k$
-formulas into exponentially (resp., polynomially) long uniform sequences of
$\hat{\Pi }^b_k$
-formulas into exponentially (resp., polynomially) long uniform sequences of
![]() $\textrm{PV}$
-provable implications between
$\textrm{PV}$
-provable implications between
![]() $\hat{\Pi }^b_k$
-formulas. Having that characterization at hand, one can use the universality of
$\hat{\Pi }^b_k$
-formulas. Having that characterization at hand, one can use the universality of
![]() $\textrm{PV}$
to employ generalized Herbrand’s theorem and push the characterization of Theorem 6 even further to witness all essentially existential quantifiers in the
$\textrm{PV}$
to employ generalized Herbrand’s theorem and push the characterization of Theorem 6 even further to witness all essentially existential quantifiers in the
![]() $\textrm{PV}$
-provable implications by polynomial-time computable functions. Instead of following this rather absolute approach, in this subsection, we will employ a relative approach to witness all the essentially existential quantifiers up to a given level
$\textrm{PV}$
-provable implications by polynomial-time computable functions. Instead of following this rather absolute approach, in this subsection, we will employ a relative approach to witness all the essentially existential quantifiers up to a given level
![]() $l \leq k$
. The idea is simple. First, by moving the
$l \leq k$
. The idea is simple. First, by moving the
![]() $\textrm{PV}$
-provable implications from
$\textrm{PV}$
-provable implications from
![]() $\textrm{PV}$
to
$\textrm{PV}$
to
![]() $\textrm{PV}_{k-l+1}$
, we will pretend that all the
$\textrm{PV}_{k-l+1}$
, we will pretend that all the
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas in
$\mathcal{L}_{\textrm{PV}}$
-formulas in
![]() $\hat{\Pi }^b_{k-l} \cup \hat{\Sigma }^b_{k-l}$
are quantifier-free in
$\hat{\Pi }^b_{k-l} \cup \hat{\Sigma }^b_{k-l}$
are quantifier-free in
![]() $\mathcal{L}_{\textrm{PV}_{k-l+1}}$
. Therefore, only
$\mathcal{L}_{\textrm{PV}_{k-l+1}}$
. Therefore, only
![]() $l$
many alternating quantifiers are left to peel off for which we use the generalized Herbrand’s theorem. In choosing the right value for
$l$
many alternating quantifiers are left to peel off for which we use the generalized Herbrand’s theorem. In choosing the right value for
![]() $l$
, there is a clear trade-off between the complexity of the witnessing functions on the one hand and the complexity of the witnessing more alternating quantifiers, on the other. For the smaller values of
$l$
, there is a clear trade-off between the complexity of the witnessing functions on the one hand and the complexity of the witnessing more alternating quantifiers, on the other. For the smaller values of
![]() $l$
, the latter would be quite easy as evidenced by Theorem 2. However, the cost to pay is the higher complexity of the witnessing functions that now live in the higher level of the polynomial hierarchy, that is, in the class
$l$
, the latter would be quite easy as evidenced by Theorem 2. However, the cost to pay is the higher complexity of the witnessing functions that now live in the higher level of the polynomial hierarchy, that is, in the class
![]() $\square ^p_{k-l+1}$
. For the higher values of
$\square ^p_{k-l+1}$
. For the higher values of
![]() $l$
, the situation is reverse. For instance, if
$l$
, the situation is reverse. For instance, if
![]() $l=k$
, then all the witnessing functions are polynomial time as they live in
$l=k$
, then all the witnessing functions are polynomial time as they live in
![]() $\textrm{PV}_{k-k+1}=\textrm{PV}$
. However, the generalized Herbrand’s theorem must witness
$\textrm{PV}_{k-k+1}=\textrm{PV}$
. However, the generalized Herbrand’s theorem must witness
![]() $k$
many quantifier alternations that is combinatorially too complex to deal with. In the present subsection, we will lean toward the lower values for
$k$
many quantifier alternations that is combinatorially too complex to deal with. In the present subsection, we will lean toward the lower values for
![]() $l$
and will only apply the relative approach to two instances of
$l$
and will only apply the relative approach to two instances of
![]() $l=1$
and
$l=1$
and
![]() $l=2$
to avoid the high witnessing complexity. However, it is worth emphasizing that the main base, that is, Theorem 6 is there and one can use it for any value of
$l=2$
to avoid the high witnessing complexity. However, it is worth emphasizing that the main base, that is, Theorem 6 is there and one can use it for any value of
![]() $l$
by employing the right instance of Herbrand’s theorem. We only cover these two cases to show that how interesting the concrete consequences can be. For
$l$
by employing the right instance of Herbrand’s theorem. We only cover these two cases to show that how interesting the concrete consequences can be. For
![]() $l=1$
, we will show that some well-known witnessing theorems in bounded arithmetic are just special cases of our witnessing theorem. For
$l=1$
, we will show that some well-known witnessing theorems in bounded arithmetic are just special cases of our witnessing theorem. For
![]() $l=2$
, the witnessing results are all new.
$l=2$
, the witnessing results are all new.
5.3.1 The game interpretation
Let
![]() $k \geq l \geq 1$
be two numbers,
$k \geq l \geq 1$
be two numbers,
![]() $G(\bar{x}, y_1, y_2, \ldots, y_l)$
be a quantifier-free
$G(\bar{x}, y_1, y_2, \ldots, y_l)$
be a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula and
$\mathcal{L}_{\textrm{PV}_k}$
-formula and
![]() $t(\bar{x})$
be an
$t(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term. We call the pair
$\mathcal{L}_{\textrm{PV}_k}$
-term. We call the pair
![]() $(G(\bar{x}, y_1, y_2, \ldots, y_l), t(\bar{x}))$
a
$(G(\bar{x}, y_1, y_2, \ldots, y_l), t(\bar{x}))$
a
![]() $(k, l)$
-game (a game, for short), and we interpret it as a uniform family of
$(k, l)$
-game (a game, for short), and we interpret it as a uniform family of
![]() $l$
-turn games between two players parameterized by the variables
$l$
-turn games between two players parameterized by the variables
![]() $\bar{x}$
. To emphasize this parameter role, we sometimes write
$\bar{x}$
. To emphasize this parameter role, we sometimes write
![]() $G_{\bar{x}}(y_1, y_2, \ldots, y_l)$
for
$G_{\bar{x}}(y_1, y_2, \ldots, y_l)$
for
![]() $G(\bar{x}, y_1, y_2, \ldots, y_l)$
and if the variables are clear from the context, we use the shorthand
$G(\bar{x}, y_1, y_2, \ldots, y_l)$
and if the variables are clear from the context, we use the shorthand
![]() $(G_{\bar{x}}, t(\bar{x}))$
for an instance of the game and
$(G_{\bar{x}}, t(\bar{x}))$
for an instance of the game and
![]() $(G, t)$
for the uniform family itself. Given the value
$(G, t)$
for the uniform family itself. Given the value
![]() $\bar{a}$
for
$\bar{a}$
for
![]() $\bar{x}$
, the game
$\bar{x}$
, the game
![]() $G_{\bar{a}}$
starts with the first player, denoted by I, playing the number
$G_{\bar{a}}$
starts with the first player, denoted by I, playing the number
![]() $b_1 \leq t(\bar{a})$
for
$b_1 \leq t(\bar{a})$
for
![]() $y_1$
. Then, the second player, denoted by II, plays
$y_1$
. Then, the second player, denoted by II, plays
![]() $b_2 \leq t(\bar{a})$
for
$b_2 \leq t(\bar{a})$
for
![]() $y_2$
and so on. The resulting tuple
$y_2$
and so on. The resulting tuple
![]() $(b_1, b_2, \ldots, b_l)$
is called a play of the game. For a play,
$(b_1, b_2, \ldots, b_l)$
is called a play of the game. For a play,
![]() $(b_1, b_2, \ldots, b_l)$
, if
$(b_1, b_2, \ldots, b_l)$
, if
![]() $G(\bar{a}, b_1, b_2, \ldots, b_l)$
holds, the first player wins the game and otherwise, the second player is the winner. A play
$G(\bar{a}, b_1, b_2, \ldots, b_l)$
holds, the first player wins the game and otherwise, the second player is the winner. A play
![]() $(b_1, \ldots, b_l)$
is called a winning play for the first (second) player, if it makes the first (second) player wins. It is an easy and well-known fact that the first player has a winning strategy in
$(b_1, \ldots, b_l)$
is called a winning play for the first (second) player, if it makes the first (second) player wins. It is an easy and well-known fact that the first player has a winning strategy in
![]() $G_{\bar{a}}$
iff
$G_{\bar{a}}$
iff
![]() $\exists y_1 \leq t(\bar{a}) \forall y_2 \leq t(\bar{a}) \exists y_3 \leq t(\bar{a}) \ldots G(\bar{a}, y_1, \ldots, y_l)$
holds. As we are always interested in the first player in this subsection, by a winning play and a winning strategy, we always mean them for the first player. Having two
$\exists y_1 \leq t(\bar{a}) \forall y_2 \leq t(\bar{a}) \exists y_3 \leq t(\bar{a}) \ldots G(\bar{a}, y_1, \ldots, y_l)$
holds. As we are always interested in the first player in this subsection, by a winning play and a winning strategy, we always mean them for the first player. Having two
![]() $(k, l)$
-games
$(k, l)$
-games
![]() $(G(\bar{x}, y_1, y_2, \ldots, y_l), t(\bar{x}))$
and
$(G(\bar{x}, y_1, y_2, \ldots, y_l), t(\bar{x}))$
and
![]() $(H(\bar{x}, z_1, z_2, \ldots, z_l), s(\bar{x}))$
, a natural question to ask is the following. Let the existence of a winning strategy in
$(H(\bar{x}, z_1, z_2, \ldots, z_l), s(\bar{x}))$
, a natural question to ask is the following. Let the existence of a winning strategy in
![]() $(G_{\bar{x}}, t(\bar{x}))$
implies the existence of a winning strategy in
$(G_{\bar{x}}, t(\bar{x}))$
implies the existence of a winning strategy in
![]() $(H_{\bar{x}}, s(\bar{x}))$
, for any
$(H_{\bar{x}}, s(\bar{x}))$
, for any
![]() $\bar{x}$
, that is, the implication
$\bar{x}$
, that is, the implication
hold. Then, does it mean that we can find an explicit way to use a winning strategy for
![]() $(G_{\bar{x}}, t(\bar{x}))$
to design a winning strategy for
$(G_{\bar{x}}, t(\bar{x}))$
to design a winning strategy for
![]() $(H_{\bar{x}}, s(\bar{x}))$
? One can even sharpen the question by asking if having a proof of the implication
$(H_{\bar{x}}, s(\bar{x}))$
? One can even sharpen the question by asking if having a proof of the implication
![]() $(\dagger )$
in the theory
$(\dagger )$
in the theory
![]() $\textrm{PV}_k$
helps to provide an explicit and relatively simple transformation between the winning strategies. Fortunately, as
$\textrm{PV}_k$
helps to provide an explicit and relatively simple transformation between the winning strategies. Fortunately, as
![]() $\textrm{PV}_k$
is a universal theory, the extraction of the explicit transformation between the winning strategies is possible, and it is simply the content of Herbrand’s theorem, Theorem 2 (up to some small modifications). We will explain the details for the two case
$\textrm{PV}_k$
is a universal theory, the extraction of the explicit transformation between the winning strategies is possible, and it is simply the content of Herbrand’s theorem, Theorem 2 (up to some small modifications). We will explain the details for the two case
![]() $l=1$
and
$l=1$
and
![]() $l=2$
, below.
$l=2$
, below.
5.3.2 The case
 $l=1$
$l=1$
Let
![]() $(G(\bar{x}, y), t(\bar{x}))$
and
$(G(\bar{x}, y), t(\bar{x}))$
and
![]() $(H(\bar{x}, z), s(\bar{x}))$
be two
$(H(\bar{x}, z), s(\bar{x}))$
be two
![]() $(k, 1)$
-games. The most trivial way to reduce the winning strategy of the latter to that of the former is via a function
$(k, 1)$
-games. The most trivial way to reduce the winning strategy of the latter to that of the former is via a function
![]() $f(\bar{x}, y)$
that maps any move
$f(\bar{x}, y)$
that maps any move
![]() $y \leq t(\bar{x})$
in
$y \leq t(\bar{x})$
in
![]() $(G, t)$
to a move
$(G, t)$
to a move
![]() $z \leq s(\bar{x})$
in
$z \leq s(\bar{x})$
in
![]() $(H, s)$
such that if the play
$(H, s)$
such that if the play
![]() $y$
is a winning play in
$y$
is a winning play in
![]() $(G, t)$
, then the play
$(G, t)$
, then the play
![]() $z=f(\bar{x}, y)$
is a winning play in
$z=f(\bar{x}, y)$
is a winning play in
![]() $(H, s)$
. Moreover, as we expect the reduction to be simple and verifiable, we expect that everything happens inside a base theory, in our case
$(H, s)$
. Moreover, as we expect the reduction to be simple and verifiable, we expect that everything happens inside a base theory, in our case
![]() $\textrm{PV}_k$
. More formally:
$\textrm{PV}_k$
. More formally:
Definition 27.
Let
![]() $(G(\bar{x}, y), t(\bar{x}))$
and
$(G(\bar{x}, y), t(\bar{x}))$
and
![]() $(H(\bar{x}, z), s(\bar{x}))$
be two
$(H(\bar{x}, z), s(\bar{x}))$
be two
![]() $(k, 1)$
-games. A
$(k, 1)$
-games. A
![]() $(k, 1)$
-reduction from
$(k, 1)$
-reduction from
![]() $(H(\bar{x}, z), s(\bar{x}))$
to
$(H(\bar{x}, z), s(\bar{x}))$
to
![]() $(G(\bar{x}, y), t(\bar{x}))$
is an
$(G(\bar{x}, y), t(\bar{x}))$
is an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $f(\bar{x}, y)$
such that:
$f(\bar{x}, y)$
such that:
-
•
 $\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
,
$\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
, -
•
 $\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [G(\bar{x}, y) \to H(\bar{x}, f(\bar{x}, y))]$
.
$\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [G(\bar{x}, y) \to H(\bar{x}, f(\bar{x}, y))]$
.
Naturally, we expect a connection between the provability of
in
![]() $\textrm{PV}_k$
and the existence of a
$\textrm{PV}_k$
and the existence of a
![]() $(k, 1)$
-reduction. This is the content of the following modification of Herbrand’s theorem.
$(k, 1)$
-reduction. This is the content of the following modification of Herbrand’s theorem.
Theorem.
For any two
![]() $(k, 1)$
-games
$(k, 1)$
-games
![]() $(G(\bar{x}, y), t(\bar{x}))$
and
$(G(\bar{x}, y), t(\bar{x}))$
and
![]() $(H(\bar{x}, z), s(\bar{x}))$
, the following are equivalent:
$(H(\bar{x}, z), s(\bar{x}))$
, the following are equivalent:
-
•
 $\textrm{PV}_k \vdash \exists y \leq t(\bar{x}) G(\bar{x}, y) \to \exists z \leq s(\bar{x}) H(\bar{x}, z)$
$\textrm{PV}_k \vdash \exists y \leq t(\bar{x}) G(\bar{x}, y) \to \exists z \leq s(\bar{x}) H(\bar{x}, z)$
-
• There is a
 $(k, 1)$
-reduction from
$(k, 1)$
-reduction from
 $(H(\bar{x}, z), s(\bar{x}))$
to
$(H(\bar{x}, z), s(\bar{x}))$
to
 $(G(\bar{x}, y), t(\bar{x}))$
.
$(G(\bar{x}, y), t(\bar{x}))$
.
Proof. One direction is trivial. For the other, assume
Therefore,
![]() $\textrm{PV}_k \vdash \forall y \exists z\, [(y \leq t(\bar{x}) \wedge G(\bar{x}, y)) \to (z \leq s(\bar{x}) \wedge H(\bar{x}, z))]$
. By Herbrand’s theorem, Theorem 2, there exists an
$\textrm{PV}_k \vdash \forall y \exists z\, [(y \leq t(\bar{x}) \wedge G(\bar{x}, y)) \to (z \leq s(\bar{x}) \wedge H(\bar{x}, z))]$
. By Herbrand’s theorem, Theorem 2, there exists an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $g(\bar{x}, y)$
such that
$g(\bar{x}, y)$
such that
Define
 \begin{equation*} f(\bar {x}, y)= \begin {cases} g(\bar {x}, y) & g(\bar {x}, y) \leq s(\bar {x})\\ 0 & g(\bar {x}, y) \gt s(\bar {x}) \end {cases} \end{equation*}
\begin{equation*} f(\bar {x}, y)= \begin {cases} g(\bar {x}, y) & g(\bar {x}, y) \leq s(\bar {x})\\ 0 & g(\bar {x}, y) \gt s(\bar {x}) \end {cases} \end{equation*}
It is easy to represent
![]() $f(\bar{x}, y)$
as an
$f(\bar{x}, y)$
as an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term. By definition, it is clear that
$\mathcal{L}_{\textrm{PV}_k}$
-term. By definition, it is clear that
![]() $\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
. Moreover, it is easy to see that
$\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
. Moreover, it is easy to see that
![]() $\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [G(\bar{x}, y) \to H(\bar{x}, f(\bar{x}, y))]$
.
$\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [G(\bar{x}, y) \to H(\bar{x}, f(\bar{x}, y))]$
.
As explained in the opening of this subsection, for
![]() $l=1$
, the combination of witnessing by
$l=1$
, the combination of witnessing by
![]() $k$
-flows, moving from
$k$
-flows, moving from
![]() $\textrm{PV}$
to
$\textrm{PV}$
to
![]() $\textrm{PV}_k$
and using Theorem 7 provides an explicit witnessing theorem for theories
$\textrm{PV}_k$
and using Theorem 7 provides an explicit witnessing theorem for theories
![]() $S^k_2$
and
$S^k_2$
and
![]() $T^k_2$
. This is what we will come back to in Corollary 30. However, as the combination has a natural form itself, it is worth defining it directly.
$T^k_2$
. This is what we will come back to in Corollary 30. However, as the combination has a natural form itself, it is worth defining it directly.
Definition 28.
Let
![]() $A(\bar{x}, y) \in \hat{\Pi }^b_{k-1}$
be an
$A(\bar{x}, y) \in \hat{\Pi }^b_{k-1}$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-formula and
$\mathcal{L}_{\textrm{PV}}$
-formula and
![]() $t(\bar{x})$
and
$t(\bar{x})$
and
![]() $r(\bar{x})$
be two
$r(\bar{x})$
be two
![]() $\mathcal{L}_{\textrm{PV}}$
-terms. By a
$\mathcal{L}_{\textrm{PV}}$
-terms. By a
![]() $\textrm{PLS}_{(k, 1)}$
-program for
$\textrm{PLS}_{(k, 1)}$
-program for
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $t(\bar{x})$
, we mean the following data: an initial
$t(\bar{x})$
, we mean the following data: an initial
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $i(\bar{x})$
, a quantifier-free
$i(\bar{x})$
, a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula
$\mathcal{L}_{\textrm{PV}_k}$
-formula
![]() $G(\bar{x}, u, z)$
, an
$G(\bar{x}, u, z)$
, an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $N(\bar{x}, u, z)$
, and an
$N(\bar{x}, u, z)$
, and an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $p(\bar{x}, z)$
, such that:
$p(\bar{x}, z)$
, such that:
-
•
 $\textrm{PV}_k \vdash i(\bar{x}) \leq s(\bar{x})$
,
$\textrm{PV}_k \vdash i(\bar{x}) \leq s(\bar{x})$
, -
•
 $\textrm{PV}_k \vdash G(\bar{x}, 0, i(\bar{x}))$
,
$\textrm{PV}_k \vdash G(\bar{x}, 0, i(\bar{x}))$
, -
•
 $\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [N(\bar{x}, u, z) \leq s(\bar{x})]$
,
$\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [N(\bar{x}, u, z) \leq s(\bar{x})]$
, -
•
 $\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) \, [G(\bar{x}, u, z) \to G(\bar{x}, u+1, N(\bar{x}, u, z))]$
,
$\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) \, [G(\bar{x}, u, z) \to G(\bar{x}, u+1, N(\bar{x}, u, z))]$
, -
•
 $\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [p(\bar{x}, z) \leq r(\bar{x})]$
,
$\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [p(\bar{x}, z) \leq r(\bar{x})]$
, -
•
 $\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [G(\bar{x}, t(\bar{x}), z) \to A(\bar{x}, p(\bar{x}, z))]$
.
$\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) [G(\bar{x}, t(\bar{x}), z) \to A(\bar{x}, p(\bar{x}, z))]$
.
By
![]() $\textrm{PLS}_{(k, 1)}$
, we mean the class of all the pairs
$\textrm{PLS}_{(k, 1)}$
, we mean the class of all the pairs
![]() $(A(\bar{x}, y), r(\bar{x}))$
for which there exists a
$(A(\bar{x}, y), r(\bar{x}))$
for which there exists a
![]() $\textrm{PLS}_{(k, 1)}$
-program. By
$\textrm{PLS}_{(k, 1)}$
-program. By
![]() $\textrm{PLS}_{(k, 1)}^p$
, we mean the class of all the pairs
$\textrm{PLS}_{(k, 1)}^p$
, we mean the class of all the pairs
![]() $(A(\bar{x}, y), r(\bar{x}))$
for which there exists a
$(A(\bar{x}, y), r(\bar{x}))$
for which there exists a
![]() $\textrm{PLS}_{(k, 1)}$
-program with a polynomial length, that is,
$\textrm{PLS}_{(k, 1)}$
-program with a polynomial length, that is,
![]() $t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
$t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
![]() $q$
.
$q$
.
It is easy to see that if
![]() $(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}_{(k, 1)}$
then
$(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}_{(k, 1)}$
then
![]() $\forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
holds and the
$\forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
holds and the
![]() $\textrm{PLS}_{(k, 1)}$
-program actually provides an algorithm to compute
$\textrm{PLS}_{(k, 1)}$
-program actually provides an algorithm to compute
![]() $y \leq r(\bar{x})$
from
$y \leq r(\bar{x})$
from
![]() $\bar{x}$
. Denoting
$\bar{x}$
. Denoting
![]() $G(\bar{x}, u, z)$
by
$G(\bar{x}, u, z)$
by
![]() $G^u$
, the algorithm starts at the zeroth level with an initial value
$G^u$
, the algorithm starts at the zeroth level with an initial value
![]() $i(\bar{x})$
bounded by
$i(\bar{x})$
bounded by
![]() $s(\bar{x})$
satisfying the property
$s(\bar{x})$
satisfying the property
![]() $G^0$
. Then, using the modification
$G^0$
. Then, using the modification
![]() $N$
, it goes from one level to the next updating any value
$N$
, it goes from one level to the next updating any value
![]() $z \leq s(\bar{x})$
with the property
$z \leq s(\bar{x})$
with the property
![]() $G^u$
to a value satisfying the property
$G^u$
to a value satisfying the property
![]() $G^{u+1}$
. Note that the modification always respects the bound
$G^{u+1}$
. Note that the modification always respects the bound
![]() $s(\bar{x})$
. Finally, reaching the level
$s(\bar{x})$
. Finally, reaching the level
![]() $t(\bar{x})$
, the algorithm uses
$t(\bar{x})$
, the algorithm uses
![]() $p$
to compute
$p$
to compute
![]() $y \leq r(\bar{x})$
satisfying
$y \leq r(\bar{x})$
satisfying
![]() $A$
from any value
$A$
from any value
![]() $z \leq s(\bar{x})$
with the property
$z \leq s(\bar{x})$
with the property
![]() $G^{t(\bar{x})}$
.
$G^{t(\bar{x})}$
.
There are two points to emphasize here. First, the case
![]() $k=1$
, where the predicate
$k=1$
, where the predicate
![]() $G(\bar{x}, y, z)$
and all the functions
$G(\bar{x}, y, z)$
and all the functions
![]() $i(\bar{x})$
,
$i(\bar{x})$
,
![]() $N(\bar{x}, u, z)$
, and
$N(\bar{x}, u, z)$
, and
![]() $p(\bar{x}, z)$
are polynomial time computable is just another presentation of the well-known polynomial local search problems, (
$p(\bar{x}, z)$
are polynomial time computable is just another presentation of the well-known polynomial local search problems, (
![]() $\textrm{PLS}$
for short), see Buss and Krajíček (Reference Buss1994); Krajíček (Reference Krajíček1995). Therefore, one can simply read
$\textrm{PLS}$
for short), see Buss and Krajíček (Reference Buss1994); Krajíček (Reference Krajíček1995). Therefore, one can simply read
![]() $\textrm{PLS}_{(k, 1)}$
-programs as a generalization of
$\textrm{PLS}_{(k, 1)}$
-programs as a generalization of
![]() $\textrm{PLS}$
from polynomial time to the
$\textrm{PLS}$
from polynomial time to the
![]() $k$
th level of the polynomial hierarchy, where the predicate
$k$
th level of the polynomial hierarchy, where the predicate
![]() $G(\bar{x}, u, z)$
and the functions
$G(\bar{x}, u, z)$
and the functions
![]() $i(\bar{x})$
,
$i(\bar{x})$
,
![]() $N(\bar{x}, u, z)$
, and
$N(\bar{x}, u, z)$
, and
![]() $p(\bar{x}, z)$
are all allowed to be on the
$p(\bar{x}, z)$
are all allowed to be on the
![]() $k$
-th level of the hierarchy. It is also worth mentioning that our
$k$
-th level of the hierarchy. It is also worth mentioning that our
![]() $\textrm{PLS}_{(k, 1)}$
-programs are similar to but weaker than
$\textrm{PLS}_{(k, 1)}$
-programs are similar to but weaker than
![]() $\Pi ^b_k-\textrm{PLS}$
problems with
$\Pi ^b_k-\textrm{PLS}$
problems with
![]() $\Pi ^b_l$
-goals defined in Beckmann and Buss (Reference Beckmann and Buss2009), where the functions
$\Pi ^b_l$
-goals defined in Beckmann and Buss (Reference Beckmann and Buss2009), where the functions
![]() $i(\bar{x})$
,
$i(\bar{x})$
,
![]() $N(\bar{x}, u, z)$
, and
$N(\bar{x}, u, z)$
, and
![]() $p(\bar{x}, z)$
(and not the predicate
$p(\bar{x}, z)$
(and not the predicate
![]() $G(\bar{x}, u, z)$
) must be polynomial-time computable and everything must be provable in
$G(\bar{x}, u, z)$
) must be polynomial-time computable and everything must be provable in
![]() $S^1_2$
rather than in
$S^1_2$
rather than in
![]() $\textrm{PV}_k$
. The second point is about the
$\textrm{PV}_k$
. The second point is about the
![]() $\textrm{PLS}^p_{(k, 1)}$
-programs with a polynomial length. For these programs, the algorithm we just provided can efficiently (relative to the level of the polynomial hierarchy, of course) compute the value of
$\textrm{PLS}^p_{(k, 1)}$
-programs with a polynomial length. For these programs, the algorithm we just provided can efficiently (relative to the level of the polynomial hierarchy, of course) compute the value of
![]() $y$
as it only needs to iterate the modification function
$y$
as it only needs to iterate the modification function
![]() $N$
for polynomially many times. In other words, we can pack the whole algorithm in one single
$N$
for polynomially many times. In other words, we can pack the whole algorithm in one single
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term as a formalized version of a
$\mathcal{L}_{\textrm{PV}_k}$
-term as a formalized version of a
![]() $\square ^p_k$
-function that computes
$\square ^p_k$
-function that computes
![]() $y$
. We will come back to this observation in Corollary 31, where we reprove a well-known witnessing theorem for
$y$
. We will come back to this observation in Corollary 31, where we reprove a well-known witnessing theorem for
![]() $S^k_2$
, characterizing the
$S^k_2$
, characterizing the
![]() $\hat{\Sigma }^b_k$
-definable functions of
$\hat{\Sigma }^b_k$
-definable functions of
![]() $S^k_2$
as the ones in the
$S^k_2$
as the ones in the
![]() $k$
th level of the polynomial hierarchy.
$k$
th level of the polynomial hierarchy.
Remark 29. Employing the game interpretation we explained before, a
![]() $\textrm{PLS}_{(k, 1)}$
program for
$\textrm{PLS}_{(k, 1)}$
program for
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $t(\bar{x})$
is nothing but the following three
$t(\bar{x})$
is nothing but the following three
![]() $(k, 1)$
-reductions:
$(k, 1)$
-reductions:
-
•
 $i(\bar{x})$
as a
$i(\bar{x})$
as a
 $(k, 1)$
-reduction from
$(k, 1)$
-reduction from
 $(G(\bar{x}, 0, z), s(\bar{x}))$
to
$(G(\bar{x}, 0, z), s(\bar{x}))$
to
 $(\top, s(\bar{x}))$
.
$(\top, s(\bar{x}))$
. -
•
 $N(\bar{x}, u, z)$
as a
$N(\bar{x}, u, z)$
as a
 $(k, 1)$
-reduction from the game
$(k, 1)$
-reduction from the game
 $(G(\bar{x}, u+1, z), s(\bar{x}))$
to the game
$(G(\bar{x}, u+1, z), s(\bar{x}))$
to the game
 $(G(\bar{x}, u, z), s(\bar{x}))$
. Notice that
$(G(\bar{x}, u, z), s(\bar{x}))$
. Notice that
 $u$
is also a parameter here.
$u$
is also a parameter here. -
•
 $p(\bar{x}, z)$
as a
$p(\bar{x}, z)$
as a
 $(k, 1)$
-reduction from the game
$(k, 1)$
-reduction from the game
 $(A(\bar{x}, y), r(\bar{x}))$
to the game
$(A(\bar{x}, y), r(\bar{x}))$
to the game
 $(G(\bar{x}, t(\bar{x}), z), s(\bar{x}))$
.
$(G(\bar{x}, t(\bar{x}), z), s(\bar{x}))$
.
Notice that the formula
![]() $A(\bar{x}, y)$
is not quantifier-free in
$A(\bar{x}, y)$
is not quantifier-free in
![]() $\mathcal{L}_{\textrm{PV}_k}$
and hence we cannot read the pair
$\mathcal{L}_{\textrm{PV}_k}$
and hence we cannot read the pair
![]() $(A(\bar{x}, y), r(\bar{x}))$
as a
$(A(\bar{x}, y), r(\bar{x}))$
as a
![]() $(k, 1)$
-game. However, as
$(k, 1)$
-game. However, as
![]() $A(\bar{x}, y)$
is in
$A(\bar{x}, y)$
is in
![]() $\hat{\Pi }^b_{k-1}$
, it is
$\hat{\Pi }^b_{k-1}$
, it is
![]() $\textrm{PV}_k$
-equivalent to a quantifier-free formula and hence we can pretend that it is quantifier-free. Having that observation, we can use Theorem 7 to see that there is a
$\textrm{PV}_k$
-equivalent to a quantifier-free formula and hence we can pretend that it is quantifier-free. Having that observation, we can use Theorem 7 to see that there is a
![]() $\textrm{PLS}_{(k, 1)}$
program for
$\textrm{PLS}_{(k, 1)}$
program for
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $t(\bar{x})$
iff there exist a quantifier-free
$t(\bar{x})$
iff there exist a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula
$\mathcal{L}_{\textrm{PV}_k}$
-formula
![]() $G(\bar{x}, u, z)$
and an
$G(\bar{x}, u, z)$
and an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $s(\bar{x})$
such that:
$s(\bar{x})$
such that:
-
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, t(\bar{x}), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, t(\bar{x}), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
.
The next Corollary uses
![]() $\textrm{PLS}_{(k, 1)}$
-programs (resp.
$\textrm{PLS}_{(k, 1)}$
-programs (resp.
![]() $\textrm{PLS}^p_{(k, 1)}$
-programs) to witness the theorems of
$\textrm{PLS}^p_{(k, 1)}$
-programs) to witness the theorems of
![]() $S^k_2$
(resp.
$S^k_2$
(resp.
![]() $T^k_2$
) as promised before.
$T^k_2$
) as promised before.
Corollary 30.
Let
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $A(\bar{x}, y) \in \hat{\Pi }^b_{k-1}$
and
$A(\bar{x}, y) \in \hat{\Pi }^b_{k-1}$
and
![]() $r(\bar{x})$
be an
$r(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-term:
$\mathcal{L}_{\textrm{PV}}$
-term:
-
(i)
 $S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
iff
$S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
iff
 $(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}^p_{(k, 1)}$
.
$(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}^p_{(k, 1)}$
. -
(ii)
 $T^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
iff
$T^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
iff
 $(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}_{(k, 1)}$
.
$(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}_{(k, 1)}$
.
Proof.
We only prove
![]() $(i)$
. The proof of
$(i)$
. The proof of
![]() $(ii)$
is similar. For the right to left direction, if there exists a
$(ii)$
is similar. For the right to left direction, if there exists a
![]() $\textrm{PLS}_{(k, 1)}$
-program for
$\textrm{PLS}_{(k, 1)}$
-program for
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $q(|\bar{x}|)$
, for some polynomial
$q(|\bar{x}|)$
, for some polynomial
![]() $q$
, using Remark 29, there are quantifier-free
$q$
, using Remark 29, there are quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula
$\mathcal{L}_{\textrm{PV}_k}$
-formula
![]() $G(\bar{x}, u, z)$
and an
$G(\bar{x}, u, z)$
and an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $s(\bar{x})$
such that:
$s(\bar{x})$
such that:
-
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
.
Since
![]() $\textrm{PV}_k$
is interpretable in
$\textrm{PV}_k$
is interpretable in
![]() $S^k_2$
, mapping all quantifier-free
$S^k_2$
, mapping all quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formulas to
$\mathcal{L}_{\textrm{PV}_k}$
-formulas to
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas in
$\mathcal{L}_{\textrm{PV}}$
-formulas in
![]() $\hat{\Sigma }^b_k$
, we can pretend that
$\hat{\Sigma }^b_k$
, we can pretend that
![]() $G(\bar{x}, u, z) \in \hat{\Sigma }^b_k$
and all the above formulas are also provable in
$G(\bar{x}, u, z) \in \hat{\Sigma }^b_k$
and all the above formulas are also provable in
![]() $S^k_2$
. Finally, since the theory
$S^k_2$
. Finally, since the theory
![]() $S^k_2$
has the axiom
$S^k_2$
has the axiom
![]() $\hat{\Sigma }^b_k-\textrm{LInd}$
and
$\hat{\Sigma }^b_k-\textrm{LInd}$
and
![]() $\exists z \leq s(\bar{x}) G(\bar{x}, u, z) \in \hat{\Sigma }^b_k$
, we have
$\exists z \leq s(\bar{x}) G(\bar{x}, u, z) \in \hat{\Sigma }^b_k$
, we have
![]() $S^k_2 \vdash \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. For the other direction, assume
$S^k_2 \vdash \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. For the other direction, assume
![]() $S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. Hence,
$S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. Hence,
![]() $S^{k}_2 \vdash \forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y) \rightarrow \bot$
. By Theorem 6,
$S^{k}_2 \vdash \forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y) \rightarrow \bot$
. By Theorem 6,
![]() $\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y) \rhd ^p_k \bot$
. Therefore, there exist a polynomial
$\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y) \rhd ^p_k \bot$
. Therefore, there exist a polynomial
![]() $q$
and a formula
$q$
and a formula
![]() $H(u, \bar{x}) \in \hat{\Pi }^b_{k}$
such that:
$H(u, \bar{x}) \in \hat{\Pi }^b_{k}$
such that:
-
•
 $\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, \bar{y})]$
.
$\textrm{PV} \vdash H(0, \bar{x}) \leftrightarrow [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, \bar{y})]$
. -
•
 $\textrm{PV} \vdash H(q(|\bar{x}|), \bar{x}) \leftrightarrow \bot$
.
$\textrm{PV} \vdash H(q(|\bar{x}|), \bar{x}) \leftrightarrow \bot$
. -
•
 $\textrm{PV} \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
$\textrm{PV} \vdash \forall u \lt q(|\bar{x}|) \; [H(u, \bar{x}) \rightarrow H(u+1, \bar{x})]$
.
Define
![]() $H'(u, \bar{x})$
as
$H'(u, \bar{x})$
as
![]() $[(u \leq q(|\bar{x}|)) \to H(u, \bar{x})]$
. It is easy to see that
$[(u \leq q(|\bar{x}|)) \to H(u, \bar{x})]$
. It is easy to see that
-
•
 $\textrm{PV} \vdash [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, \bar{y})] \to H'(0, \bar{x})$
.
$\textrm{PV} \vdash [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, \bar{y})] \to H'(0, \bar{x})$
. -
•
 $\textrm{PV} \vdash H'(q(|\bar{x}|), \bar{x}) \to \bot$
.
$\textrm{PV} \vdash H'(q(|\bar{x}|), \bar{x}) \to \bot$
. -
•
 $\textrm{PV} \vdash H'(u, \bar{x}) \rightarrow H'(u+1, \bar{x})$
.
$\textrm{PV} \vdash H'(u, \bar{x}) \rightarrow H'(u+1, \bar{x})$
.
As
![]() $\textrm{PV}$
has the pairing function, it can encode finite many bounded variables as one bounded variable. Hence, without loss of generality, we can assume that
$\textrm{PV}$
has the pairing function, it can encode finite many bounded variables as one bounded variable. Hence, without loss of generality, we can assume that
![]() $H'$
is in the prenex bounded form starting with one universal quantifier on
$H'$
is in the prenex bounded form starting with one universal quantifier on
![]() $z$
, that is,
$z$
, that is,
![]() $H'(u, \bar{x})=\forall z \leq s'(\bar{x}, u) \; I(\bar{x}, u, z)$
, where
$H'(u, \bar{x})=\forall z \leq s'(\bar{x}, u) \; I(\bar{x}, u, z)$
, where
![]() $s'$
is
$s'$
is
![]() $\textrm{PV}$
-monotone and
$\textrm{PV}$
-monotone and
![]() $I \in \hat{\Sigma }^b_{k-1}$
. Define
$I \in \hat{\Sigma }^b_{k-1}$
. Define
![]() $s(\bar{x})$
as
$s(\bar{x})$
as
![]() $s'(q(|\bar{x}|), \bar{x})$
. Then, it is easy to see that
$s'(q(|\bar{x}|), \bar{x})$
. Then, it is easy to see that
Hence, without loss of generality, we can assume that
![]() $H'$
is in the form
$H'$
is in the form
![]() $\forall z \leq s(\bar{x}) J(\bar{x}, u, z)$
, where
$\forall z \leq s(\bar{x}) J(\bar{x}, u, z)$
, where
![]() $J$
is in
$J$
is in
![]() $\hat{\Sigma }^b_{k-1}$
. Since
$\hat{\Sigma }^b_{k-1}$
. Since
![]() $\textrm{PV}$
is a subtheory of
$\textrm{PV}$
is a subtheory of
![]() $\textrm{PV}_{k}$
and in
$\textrm{PV}_{k}$
and in
![]() $\textrm{PV}_{k}$
any formula in
$\textrm{PV}_{k}$
any formula in
![]() $\hat{\Sigma }^b_{k-1}$
is equivalent to a quantifier-free formula, we can assume that
$\hat{\Sigma }^b_{k-1}$
is equivalent to a quantifier-free formula, we can assume that
![]() $J$
is quantifier-free in the language of
$J$
is quantifier-free in the language of
![]() $\textrm{PV}_{k}$
and we have
$\textrm{PV}_{k}$
and we have
-
•
 $\textrm{PV}_{k} \vdash [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y)] \to \forall z \leq s(\bar{x}) J(\bar{x}, 0, z)$
.
$\textrm{PV}_{k} \vdash [\forall y \leq r(\bar{x}) \; \neg A(\bar{x}, y)] \to \forall z \leq s(\bar{x}) J(\bar{x}, 0, z)$
. -
•
 $\textrm{PV}_{k} \vdash \forall z \leq s(\bar{x}) J(\bar{x}, q(|\bar{x}|), z) \to \bot$
.
$\textrm{PV}_{k} \vdash \forall z \leq s(\bar{x}) J(\bar{x}, q(|\bar{x}|), z) \to \bot$
. -
•
 $\textrm{PV}_{k} \vdash \forall z \leq s(\bar{x}) J(\bar{x}, u, z) \rightarrow \forall z \leq s(\bar{x}) J(\bar{x}, u+1, z)$
.
$\textrm{PV}_{k} \vdash \forall z \leq s(\bar{x}) J(\bar{x}, u, z) \rightarrow \forall z \leq s(\bar{x}) J(\bar{x}, u+1, z)$
.
Define
![]() $G(\bar{x}, u, z)$
as
$G(\bar{x}, u, z)$
as
![]() $\neg J(\bar{x}, q(|\bar{x}|) \dot{-} u, z)$
and note that it is a quantifier-free
$\neg J(\bar{x}, q(|\bar{x}|) \dot{-} u, z)$
and note that it is a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula. Therefore, we have
$\mathcal{L}_{\textrm{PV}_k}$
-formula. Therefore, we have
-
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), z) \to \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, 0, z)$
. -
•
 $\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
.
$\textrm{PV}_{k} \vdash \exists z \leq s(\bar{x}) G(\bar{x}, u, z) \rightarrow \exists z \leq s(\bar{x}) G(\bar{x}, u+1, z)$
.
Finally, it is enough to use Remark 29 to get a
![]() $\textrm{PLS}_{(k, 1)}$
-program for the pair
$\textrm{PLS}_{(k, 1)}$
-program for the pair
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $q(|\bar{x}|)$
. Hence,
$q(|\bar{x}|)$
. Hence,
![]() $(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}^p_{(k, 1)}$
.
$(A(\bar{x}, y), r(\bar{x})) \in \textrm{PLS}^p_{(k, 1)}$
.
Note that the second part in Corollary 30, when applied on
![]() $k=1$
, reproves the well-known characterization of the
$k=1$
, reproves the well-known characterization of the
![]() $T^1_2$
-provable formulas of the form
$T^1_2$
-provable formulas of the form
![]() $\forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
, where
$\forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
, where
![]() $A(\bar{x}, y) \in \hat{\Pi }^b_0$
, in terms of the usual
$A(\bar{x}, y) \in \hat{\Pi }^b_0$
, in terms of the usual
![]() $\textrm{PLS}$
problems (Buss and Krajíček Reference Buss and Krajíček1994; Krajíček Reference Krajíček1995). Our result, however, seems a bit weaker than the one proved in Buss and Krajíček (Reference Buss and Krajíček1994), Krajíček (Reference Krajíček1995), as in the latter
$\textrm{PLS}$
problems (Buss and Krajíček Reference Buss and Krajíček1994; Krajíček Reference Krajíček1995). Our result, however, seems a bit weaker than the one proved in Buss and Krajíček (Reference Buss and Krajíček1994), Krajíček (Reference Krajíček1995), as in the latter
![]() $y$
is not assumed to be bounded and
$y$
is not assumed to be bounded and
![]() $A(\bar{x}, y)$
can be in
$A(\bar{x}, y)$
can be in
![]() $\hat{\Sigma }^b_1$
rather than in our lower class of
$\hat{\Sigma }^b_1$
rather than in our lower class of
![]() $\hat{\Pi }^b_0$
. However, proving the stronger form from the one we provided is just a standard technique. First, notice that the presence of
$\hat{\Pi }^b_0$
. However, proving the stronger form from the one we provided is just a standard technique. First, notice that the presence of
![]() $r(\bar{x})$
is no restriction, thanks to Parikh theorem. Second, to reduce the complexity of
$r(\bar{x})$
is no restriction, thanks to Parikh theorem. Second, to reduce the complexity of
![]() $A(\bar{x}, y)$
, it is enough to write
$A(\bar{x}, y)$
, it is enough to write
![]() $A(\bar{x}, y)$
in the form
$A(\bar{x}, y)$
in the form
![]() $\exists \bar{z} \leq \bar{x}(\bar{x}) B(\bar{x}, y, \bar{z})$
, where
$\exists \bar{z} \leq \bar{x}(\bar{x}) B(\bar{x}, y, \bar{z})$
, where
![]() $B(\bar{x}, y, \bar{z}) \in \hat{\Pi }^b_0$
. Then, using the pairing function available in
$B(\bar{x}, y, \bar{z}) \in \hat{\Pi }^b_0$
. Then, using the pairing function available in
![]() $\textrm{PV}$
, we can make
$\textrm{PV}$
, we can make
![]() $y$
and all the variables
$y$
and all the variables
![]() $\bar{z}$
into one bounded variable
$\bar{z}$
into one bounded variable
![]() $w \leq t(\bar{x})$
. Now, we can apply Corollary 30 to compute
$w \leq t(\bar{x})$
. Now, we can apply Corollary 30 to compute
![]() $w$
by a
$w$
by a
![]() $\textrm{PLS}_{(k, 1)}$
-program. With this technique, the
$\textrm{PLS}_{(k, 1)}$
-program. With this technique, the
![]() $\textrm{PLS}_{(k, 1)}$
-program not only computes the intended variable
$\textrm{PLS}_{(k, 1)}$
-program not only computes the intended variable
![]() $y$
but it also finds a value for the variables
$y$
but it also finds a value for the variables
![]() $\bar{z}$
. To retrieve our formula
$\bar{z}$
. To retrieve our formula
![]() $A(\bar{x}, y)$
, we can simply keep the computation for
$A(\bar{x}, y)$
, we can simply keep the computation for
![]() $y$
and forget the other values for
$y$
and forget the other values for
![]() $\bar{z}$
by reintroducing their existential quantifiers. Having this observation about the usual
$\bar{z}$
by reintroducing their existential quantifiers. Having this observation about the usual
![]() $\textrm{PLS}$
, one can read Corollary 30 as a generalization of the mentioned characterization for
$\textrm{PLS}$
, one can read Corollary 30 as a generalization of the mentioned characterization for
![]() $T^1_2$
to cover both
$T^1_2$
to cover both
![]() $T^k_2$
and
$T^k_2$
and
![]() $S^k_2$
, for any
$S^k_2$
, for any
![]() $k \geq 1$
. However, the latter case can be strengthened even further as the polynomial
$k \geq 1$
. However, the latter case can be strengthened even further as the polynomial
![]() $\textrm{PLS}_{(k, 1)}$
-program provided in Corollary 30 can be simplified to one single
$\textrm{PLS}_{(k, 1)}$
-program provided in Corollary 30 can be simplified to one single
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term. This reproves the following well-known witnessing theorem for
$\mathcal{L}_{\textrm{PV}_k}$
-term. This reproves the following well-known witnessing theorem for
![]() $S^k_2$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995).
$S^k_2$
(Buss Reference Buss1986; Krajíček Reference Krajíček1995).
Corollary 31.
The provably
![]() $\hat{\Sigma }^b_k$
-definable functions of
$\hat{\Sigma }^b_k$
-definable functions of
![]() $S_2^k$
are in
$S_2^k$
are in
![]() $\square _{k}^p$
. Even better, if
$\square _{k}^p$
. Even better, if
![]() $S^k_2 \vdash \forall \bar{x} \exists y A(\bar{x}, y)$
, where
$S^k_2 \vdash \forall \bar{x} \exists y A(\bar{x}, y)$
, where
![]() $A(\bar{x}, y) \in \hat{\Sigma }^b_k$
, then there exists a function
$A(\bar{x}, y) \in \hat{\Sigma }^b_k$
, then there exists a function
![]() $f \in \square _k^p$
represented as an
$f \in \square _k^p$
represented as an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term such that
$\mathcal{L}_{\textrm{PV}_k}$
-term such that
![]() $\textrm{PV}_k \vdash \forall \bar{x} \, A(\bar{x}, f(\bar{x}))$
.
$\textrm{PV}_k \vdash \forall \bar{x} \, A(\bar{x}, f(\bar{x}))$
.
Proof.
Following the technique we just described, without loss of generality, we can assume that
![]() $A(\bar{x}, y)$
has no existential quantifier in its front and hence it is actually in
$A(\bar{x}, y)$
has no existential quantifier in its front and hence it is actually in
![]() $\hat{\Pi }^{b}_{k-1}$
. By Parikh theorem, there exists an
$\hat{\Pi }^{b}_{k-1}$
. By Parikh theorem, there exists an
![]() $\mathcal{L}_{\textrm{PV}}$
-term
$\mathcal{L}_{\textrm{PV}}$
-term
![]() $r(\bar{x})$
such that
$r(\bar{x})$
such that
![]() $S^k_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. By Corollary 30, there exists a
$S^k_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) A(\bar{x}, y)$
. By Corollary 30, there exists a
![]() $\textrm{PLS}_{(k, 1)}$
-program for
$\textrm{PLS}_{(k, 1)}$
-program for
![]() $(A(\bar{x}, y), r(\bar{x}))$
with the length
$(A(\bar{x}, y), r(\bar{x}))$
with the length
![]() $q(|\bar{x}|)$
, for a polynomial
$q(|\bar{x}|)$
, for a polynomial
![]() $q$
. Let
$q$
. Let
![]() $G(\bar{x}, u, z)$
,
$G(\bar{x}, u, z)$
,
![]() $i(\bar{x})$
,
$i(\bar{x})$
,
![]() $N(\bar{x}, u, z)$
, and
$N(\bar{x}, u, z)$
, and
![]() $p(\bar{x}, z)$
be the data of the
$p(\bar{x}, z)$
be the data of the
![]() $\textrm{PLS}_{(k, 1)}$
-program. By recursion on notation on
$\textrm{PLS}_{(k, 1)}$
-program. By recursion on notation on
![]() $w$
, define the function
$w$
, define the function
![]() $M(w, \bar{x})$
as
$M(w, \bar{x})$
as
 \begin{equation*} \begin {cases} M(0, \bar {x})=i(\bar {x}) & \\ M(w, \bar {x})=N(\bar {x}, |w| \dot {-} 1, M(\lfloor \frac {w}{2} \rfloor, \bar {x})) & w \gt 0\\ \end {cases} \end{equation*}
\begin{equation*} \begin {cases} M(0, \bar {x})=i(\bar {x}) & \\ M(w, \bar {x})=N(\bar {x}, |w| \dot {-} 1, M(\lfloor \frac {w}{2} \rfloor, \bar {x})) & w \gt 0\\ \end {cases} \end{equation*}
Recall that the
![]() $\mathcal{L}_{\textrm{PV}_k}$
-terms are closed under bounded recursion on notation. As both
$\mathcal{L}_{\textrm{PV}_k}$
-terms are closed under bounded recursion on notation. As both
![]() $i$
and
$i$
and
![]() $N$
are
$N$
are
![]() $\mathcal{L}_{\textrm{PV}_k}$
-terms and
$\mathcal{L}_{\textrm{PV}_k}$
-terms and
![]() $i(\bar{x})$
is bounded by
$i(\bar{x})$
is bounded by
![]() $s(\bar{x})$
and
$s(\bar{x})$
and
![]() $N(\bar{x}, u, z)$
maps any
$N(\bar{x}, u, z)$
maps any
![]() $z \leq s(\bar{x})$
to something below
$z \leq s(\bar{x})$
to something below
![]() $s(\bar{x})$
, we can make sure that the function
$s(\bar{x})$
, we can make sure that the function
![]() $M(w, \bar{x})$
is also representable as an
$M(w, \bar{x})$
is also representable as an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term. Now, define
$\mathcal{L}_{\textrm{PV}_k}$
-term. Now, define
![]() $I(\bar{x}, w, z)$
as
$I(\bar{x}, w, z)$
as
![]() $G(\bar{x}, |w|, z)$
. Using the properties of the
$G(\bar{x}, |w|, z)$
. Using the properties of the
![]() $\textrm{PLS}_{(k, 1)}$
-program, it is clear that
$\textrm{PLS}_{(k, 1)}$
-program, it is clear that
-
•
 $\textrm{PV}_k \vdash I(\bar{x}, 0, i(\bar{x}))$
,
$\textrm{PV}_k \vdash I(\bar{x}, 0, i(\bar{x}))$
, -
•
 $\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) \forall w \gt 0 \, [I(\bar{x}, \lfloor \frac{w}{2} \rfloor, z) \to I(\bar{x}, w, N(\bar{x}, |w| \dot{-} 1, z))]$
.
$\textrm{PV}_k \vdash \forall z \leq s(\bar{x}) \forall w \gt 0 \, [I(\bar{x}, \lfloor \frac{w}{2} \rfloor, z) \to I(\bar{x}, w, N(\bar{x}, |w| \dot{-} 1, z))]$
.
Therefore, as
![]() $\textrm{PV}_k \vdash M(w, \bar{x}) \leq s(\bar{x})$
, by using the axiom
$\textrm{PV}_k \vdash M(w, \bar{x}) \leq s(\bar{x})$
, by using the axiom
![]() $\textrm{PInd}$
on the quantifier-free formula
$\textrm{PInd}$
on the quantifier-free formula
![]() $I(\bar{x}, w, M(w, \bar{x}))$
, we can prove
$I(\bar{x}, w, M(w, \bar{x}))$
, we can prove
![]() $\textrm{PV}_k \vdash I(\bar{x}, w, M(w, \bar{x}))$
. Substituting
$\textrm{PV}_k \vdash I(\bar{x}, w, M(w, \bar{x}))$
. Substituting
![]() $w=\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor$
, we reach
$w=\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor$
, we reach
Using the fact that
![]() $\textrm{PV}_k \vdash |\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor |=q(|\bar{x}|)$
, we have
$\textrm{PV}_k \vdash |\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor |=q(|\bar{x}|)$
, we have
Therefore, as
![]() $p(\bar{x}, z)$
is an
$p(\bar{x}, z)$
is an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term and it has the property
$\mathcal{L}_{\textrm{PV}_k}$
-term and it has the property
we can define
![]() $f(\bar{x})=p(\bar{x}, M(\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor, \bar{x}))$
as an
$f(\bar{x})=p(\bar{x}, M(\lfloor \frac{2^{q(|\bar{x}|)}}{2} \rfloor, \bar{x}))$
as an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term. Therefore,
$\mathcal{L}_{\textrm{PV}_k}$
-term. Therefore,
![]() $\textrm{PV}_k \vdash \forall \bar{x} A(\bar{x}, f(\bar{x}))$
.
$\textrm{PV}_k \vdash \forall \bar{x} A(\bar{x}, f(\bar{x}))$
.
5.3.3 The case
 $l=2$
$l=2$
Let
![]() $(G(\bar{x}, y, z), t(\bar{x}))$
and
$(G(\bar{x}, y, z), t(\bar{x}))$
and
![]() $(H(\bar{x}, v, w), s(\bar{x}))$
be two
$(H(\bar{x}, v, w), s(\bar{x}))$
be two
![]() $(k, 2)$
-games. To use a winning strategy for
$(k, 2)$
-games. To use a winning strategy for
![]() $(G(\bar{x}, y, z), t(\bar{x}))$
to design one for
$(G(\bar{x}, y, z), t(\bar{x}))$
to design one for
![]() $(H(\bar{x}, v, w), s(\bar{x}))$
, the most trivial way is using two functions
$(H(\bar{x}, v, w), s(\bar{x}))$
, the most trivial way is using two functions
![]() $f(\bar{x}, y)$
and
$f(\bar{x}, y)$
and
![]() $g(\bar{x}, y, w)$
, where
$g(\bar{x}, y, w)$
, where
![]() $f(\bar{x}, y)$
reads the first move
$f(\bar{x}, y)$
reads the first move
![]() $y \leq t(\bar{x})$
in
$y \leq t(\bar{x})$
in
![]() $(G, t)$
and computes a first move
$(G, t)$
and computes a first move
![]() $v \leq s(\bar{x})$
in
$v \leq s(\bar{x})$
in
![]() $(H, s)$
. Then,
$(H, s)$
. Then,
![]() $g(\bar{x}, y, w)$
reads the second move
$g(\bar{x}, y, w)$
reads the second move
![]() $w \leq s(\bar{x})$
in
$w \leq s(\bar{x})$
in
![]() $(H, s)$
and computes a second move
$(H, s)$
and computes a second move
![]() $z \leq t(\bar{x})$
in
$z \leq t(\bar{x})$
in
![]() $(G, t)$
. These computations must be in a way that if the play
$(G, t)$
. These computations must be in a way that if the play
![]() $(y, z)$
is winning in
$(y, z)$
is winning in
![]() $(G, t)$
, the play
$(G, t)$
, the play
![]() $(v, w)$
is winning in
$(v, w)$
is winning in
![]() $(H, t)$
. Expecting the whole reduction process to be simple relative to
$(H, t)$
. Expecting the whole reduction process to be simple relative to
![]() $\textrm{PV}_k$
, we have:
$\textrm{PV}_k$
, we have:
Definition 32.
Let
![]() $(G(\bar{x}, y, z), t(\bar{x}))$
and
$(G(\bar{x}, y, z), t(\bar{x}))$
and
![]() $(H(\bar{x}, v, w), s(\bar{x}))$
be two
$(H(\bar{x}, v, w), s(\bar{x}))$
be two
![]() $(k, 2)$
-games. By a deterministic
$(k, 2)$
-games. By a deterministic
![]() $(k, 2)$
-reduction from
$(k, 2)$
-reduction from
![]() $(H, s)$
to
$(H, s)$
to
![]() $(G, t)$
, we mean two
$(G, t)$
, we mean two
![]() $\mathcal{L}_{\textrm{PV}_k}$
-terms
$\mathcal{L}_{\textrm{PV}_k}$
-terms
![]() $f(\bar{x}, y)$
and
$f(\bar{x}, y)$
and
![]() $g(\bar{x}, y, w)$
such that:
$g(\bar{x}, y, w)$
such that:
-
•
 $\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
.
$\textrm{PV}_k \vdash \forall y \leq t(\bar{x}) [f(\bar{x}, y) \leq s(\bar{x})]$
. -
•
 $\textrm{PV}_k \vdash \forall w \leq s(\bar{x}) \forall y \leq t(\bar{x}) [g(\bar{x}, y, w) \leq t(\bar{x})]$
.
$\textrm{PV}_k \vdash \forall w \leq s(\bar{x}) \forall y \leq t(\bar{x}) [g(\bar{x}, y, w) \leq t(\bar{x})]$
. -
•
 $\textrm{PV}_k \vdash \forall w \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w)) \to H(\bar{x}, f(\bar{x}, y), w)]$
.
$\textrm{PV}_k \vdash \forall w \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w)) \to H(\bar{x}, f(\bar{x}, y), w)]$
.
In a similar fashion to what we had n the previous subsubsection, we expect an equivalence between the provability of
in
![]() $\textrm{PV}_k$
and the existence of a deterministic
$\textrm{PV}_k$
and the existence of a deterministic
![]() $(k, 2)$
-reduction from
$(k, 2)$
-reduction from
![]() $(H, s)$
to
$(H, s)$
to
![]() $(G, t)$
. Unfortunately, this expected equivalence does not exist, unless a hardness conjecture in complexity theory fails. Let us first explain this conjecture.
$(G, t)$
. Unfortunately, this expected equivalence does not exist, unless a hardness conjecture in complexity theory fails. Let us first explain this conjecture.
Let
![]() $U, V \subseteq \mathbb{N}$
be two disjoint
$U, V \subseteq \mathbb{N}$
be two disjoint
![]() $\textbf{NP}$
-sets. We call a polynomial time computable
$\textbf{NP}$
-sets. We call a polynomial time computable
![]() $S \subseteq \mathbb{N}$
a separator for
$S \subseteq \mathbb{N}$
a separator for
![]() $U$
and
$U$
and
![]() $V$
, if
$V$
, if
![]() $U \subseteq S$
and
$U \subseteq S$
and
![]() $S \cap V=\varnothing$
. The hardness conjecture we want to use states that there are two disjoint
$S \cap V=\varnothing$
. The hardness conjecture we want to use states that there are two disjoint
![]() $\textbf{NP}$
-sets
$\textbf{NP}$
-sets
![]() $U$
and
$U$
and
![]() $V$
that have no separator.
$V$
that have no separator.
Example 33.
Let
![]() $U$
and
$U$
and
![]() $V$
be two disjoint
$V$
be two disjoint
![]() $\textbf{NP}$
-sets that have no separator and represent them by the
$\textbf{NP}$
-sets that have no separator and represent them by the
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas
$\mathcal{L}_{\textrm{PV}}$
-formulas
![]() $\exists y \leq s_B(x) B(x, y)$
and
$\exists y \leq s_B(x) B(x, y)$
and
![]() $\exists y \leq s_C(x) C(x, y)$
, respectively, where
$\exists y \leq s_C(x) C(x, y)$
, respectively, where
![]() $B(x, y)$
and
$B(x, y)$
and
![]() $C(x, z)$
are two quantifier-free
$C(x, z)$
are two quantifier-free
![]() $\mathcal{L}_{\textrm{PV}}$
-formulas and
$\mathcal{L}_{\textrm{PV}}$
-formulas and
![]() $s_B(x)$
and
$s_B(x)$
and
![]() $s_C(x)$
are two
$s_C(x)$
are two
![]() $\mathcal{L}_{\textrm{PV}}$
-terms. First, notice that without loss of generality, we can always assume that
$\mathcal{L}_{\textrm{PV}}$
-terms. First, notice that without loss of generality, we can always assume that
![]() $s_B(x)=s_C(x)$
and
$s_B(x)=s_C(x)$
and
![]() $\forall x (s_B(x) \gt 0)$
holds in the standard model. The reason is that we can replace
$\forall x (s_B(x) \gt 0)$
holds in the standard model. The reason is that we can replace
![]() $\exists y \leq s_B(x) B(x, y)$
by
$\exists y \leq s_B(x) B(x, y)$
by
and similarly for
![]() $\exists z \leq s_C(x) C(x, z)$
. From now on, denote both
$\exists z \leq s_C(x) C(x, z)$
. From now on, denote both
![]() $s_B(x)$
and
$s_B(x)$
and
![]() $s_C(x)$
, by the common name
$s_C(x)$
, by the common name
![]() $s(x)$
. Moreover, notice that as
$s(x)$
. Moreover, notice that as
![]() $U \cap V=\varnothing$
, the formula
$U \cap V=\varnothing$
, the formula
![]() $\forall y \leq s(x) \neg B(x, y) \vee \forall z \leq s(x) \neg C(x, z)$
is true, for any value for
$\forall y \leq s(x) \neg B(x, y) \vee \forall z \leq s(x) \neg C(x, z)$
is true, for any value for
![]() $x$
. Now, let
$x$
. Now, let
It is clear that the formula
logically implies
![]() $ \exists w \leq s(x) \forall yz \leq s(x) \; A(x, w, y, z)$
and hence the implication is provable in
$ \exists w \leq s(x) \forall yz \leq s(x) \; A(x, w, y, z)$
and hence the implication is provable in
![]() $\textrm{PV}$
. Unfortunately, in both formulas, some of the quantifier blocks have more than one bounded quantifiers, and hence, the formulas cannot be read as
$\textrm{PV}$
. Unfortunately, in both formulas, some of the quantifier blocks have more than one bounded quantifiers, and hence, the formulas cannot be read as
![]() $(k, 2)$
-games. However, using the pairing function and its projections available in
$(k, 2)$
-games. However, using the pairing function and its projections available in
![]() $\textrm{PV}$
, it is not hard to change the formulas to
$\textrm{PV}$
, it is not hard to change the formulas to
![]() $\textrm{PV}$
-equivalent formulas in the right form. We will avoid applying this change here as it makes everything unnecessarily complicated. Instead, we keep working with the original formulas as the one and the only exception in this paper. However, let us emphasize that whatever we claim in this example can be rewritten in a precise way using the mentioned encoding. Having said that, in the rest of this example, we pretend that we are working with the two
$\textrm{PV}$
-equivalent formulas in the right form. We will avoid applying this change here as it makes everything unnecessarily complicated. Instead, we keep working with the original formulas as the one and the only exception in this paper. However, let us emphasize that whatever we claim in this example can be rewritten in a precise way using the mentioned encoding. Having said that, in the rest of this example, we pretend that we are working with the two
![]() $(k, 2)$
-games
$(k, 2)$
-games
![]() $(A(x, w, y, z), s(x))$
and
$(A(x, w, y, z), s(x))$
and
![]() $(A(x, w_0, y_0, z_0) \vee A(x, w_1, y_1, z_1), s(x))$
and we show that there is no deterministic
$(A(x, w_0, y_0, z_0) \vee A(x, w_1, y_1, z_1), s(x))$
and we show that there is no deterministic
![]() $(k, 2)$
-reduction from the
$(k, 2)$
-reduction from the
![]() $(k, 2)$
-game
$(k, 2)$
-game
![]() $(A(x, w, y, z), s(x))$
to the
$(A(x, w, y, z), s(x))$
to the
![]() $(k, 2)$
-game
$(k, 2)$
-game
![]() $(A(x, w_0, y_0, z_0) \vee A(x, w_1, y_1, z_1), s(x))$
. For the sake of contradiction, assume that there are polynomial time computable functions
$(A(x, w_0, y_0, z_0) \vee A(x, w_1, y_1, z_1), s(x))$
. For the sake of contradiction, assume that there are polynomial time computable functions
![]() $f(x, w_0, w_1)$
,
$f(x, w_0, w_1)$
,
![]() $g_0(x, w_0, w_1, y, z)$
,
$g_0(x, w_0, w_1, y, z)$
,
![]() $g_1(x, w_0, w_1, y, z)$
,
$g_1(x, w_0, w_1, y, z)$
,
![]() $h_0(x, w_0, w_1, y, z)$
, and finally
$h_0(x, w_0, w_1, y, z)$
, and finally
![]() $h_1(x, w_0, w_1, y, z)$
, all represented as
$h_1(x, w_0, w_1, y, z)$
, all represented as
![]() $\mathcal{L}_{\textrm{PV}}$
-terms such that they read
$\mathcal{L}_{\textrm{PV}}$
-terms such that they read
![]() $w_0$
,
$w_0$
,
![]() $w_1$
,
$w_1$
,
![]() $y$
, and
$y$
, and
![]() $z$
below
$z$
below
![]() $s(x)$
and compute
$s(x)$
and compute
![]() $w$
,
$w$
,
![]() $y_0$
,
$y_0$
,
![]() $y_1$
,
$y_1$
,
![]() $z_0$
, and
$z_0$
, and
![]() $z_1$
all below
$z_1$
all below
![]() $s(x)$
, respectively, satisfying the property
$s(x)$
, respectively, satisfying the property
(The arguments of the functions are omitted, for simplicity). Therefore, the formula
is true in the standard model. Substitute
![]() $w_0=0$
and
$w_0=0$
and
![]() $w_1=1$
and notice that the condition
$w_1=1$
and notice that the condition
![]() $s(x) \geq 1$
allows such a substitution. We see that
$s(x) \geq 1$
allows such a substitution. We see that
![]() $A(x, 0, g_0, h_0)$
is equivalent to
$A(x, 0, g_0, h_0)$
is equivalent to
![]() $\neg B(x, g_0)$
and
$\neg B(x, g_0)$
and
![]() $A(x, 1, g_1, h_1)$
is equivalent to
$A(x, 1, g_1, h_1)$
is equivalent to
![]() $\neg C(x, h_1)$
. Therefore, the following formula is true:
$\neg C(x, h_1)$
. Therefore, the following formula is true:
Therefore, we have
Recall that as
![]() $U \cap V=\varnothing$
, we know
$U \cap V=\varnothing$
, we know
![]() $\forall y \leq s(x) \neg B(x, y) \vee \forall z \leq s(x) \neg C(x, z)$
is true. Therefore, we reach
$\forall y \leq s(x) \neg B(x, y) \vee \forall z \leq s(x) \neg C(x, z)$
is true. Therefore, we reach
![]() $\forall yz \leq s(x) A(x, f, y, z)$
. Now, note that if
$\forall yz \leq s(x) A(x, f, y, z)$
. Now, note that if
![]() $f(x, 0, 1)=0$
, the formula
$f(x, 0, 1)=0$
, the formula
![]() $A(x, f, y, z)$
is equivalent to
$A(x, f, y, z)$
is equivalent to
![]() $\neg B(x, y)$
and if
$\neg B(x, y)$
and if
![]() $f(x, 0, 1) \neq 0$
, it is equivalent to
$f(x, 0, 1) \neq 0$
, it is equivalent to
![]() $\neg C(x, z)$
. Therefore, if
$\neg C(x, z)$
. Therefore, if
![]() $f(x, 0, 1)=0$
, we have
$f(x, 0, 1)=0$
, we have
![]() $\forall y \leq s(x) \neg B(x, y)$
and if
$\forall y \leq s(x) \neg B(x, y)$
and if
![]() $f(x, 0, 1) \neq 0$
, we have
$f(x, 0, 1) \neq 0$
, we have
![]() $\forall z \leq s(x) \neg C(x, z)$
. We claim that the set
$\forall z \leq s(x) \neg C(x, z)$
. We claim that the set
![]() $S=\{x \in \mathbb{N} \mid f(x) \neq 0\}$
is a separator. First, note that
$S=\{x \in \mathbb{N} \mid f(x) \neq 0\}$
is a separator. First, note that
![]() $S$
is polynomial computable as
$S$
is polynomial computable as
![]() $f(x, w_0, w_1)$
is a polynomial-time computable function. Second, it is clear that
$f(x, w_0, w_1)$
is a polynomial-time computable function. Second, it is clear that
![]() $S$
is disjoint from
$S$
is disjoint from
![]() $V$
. To show that it includes
$V$
. To show that it includes
![]() $U$
, assume
$U$
, assume
![]() $x \in U$
and
$x \in U$
and
![]() $f(x, 0, 1)=0$
. Then,
$f(x, 0, 1)=0$
. Then,
![]() $\forall y \leq s(x) \neg B(x, y)$
which means that
$\forall y \leq s(x) \neg B(x, y)$
which means that
![]() $x \notin U$
. Therefore, we found a separator which is impossible. Hence, the claimed deterministic
$x \notin U$
. Therefore, we found a separator which is impossible. Hence, the claimed deterministic
![]() $(k, 2)$
-reduction does not exist.
$(k, 2)$
-reduction does not exist.
As we observed in Example 33, deterministic
![]() $(k, 2)$
-reductions are not even powerful enough to capture the pure logical implications between the existence of the winning strategies. To solve the problem, in the following, we strengthen the notion by relaxing the determinism in the definition.
$(k, 2)$
-reductions are not even powerful enough to capture the pure logical implications between the existence of the winning strategies. To solve the problem, in the following, we strengthen the notion by relaxing the determinism in the definition.
Definition 34.
Let
![]() $(G(\bar{x}, y, z), t(\bar{x}))$
and
$(G(\bar{x}, y, z), t(\bar{x}))$
and
![]() $(H(\bar{x}, v, w), s(\bar{x}))$
be two
$(H(\bar{x}, v, w), s(\bar{x}))$
be two
![]() $(k, 2)$
-games. By a
$(k, 2)$
-games. By a
![]() $(k, 2)$
-reduction from
$(k, 2)$
-reduction from
![]() $(H, s)$
to
$(H, s)$
to
![]() $(G, t)$
, we mean a finite sequence of
$(G, t)$
, we mean a finite sequence of
![]() $\mathcal{L}_{\textrm{PV}_k}$
-terms
$\mathcal{L}_{\textrm{PV}_k}$
-terms
![]() $f_0(\bar{x}, y)$
,
$f_0(\bar{x}, y)$
,
![]() $f_1(\bar{x}, y, w_0)$
, …,
$f_1(\bar{x}, y, w_0)$
, …,
![]() $f_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
together with an
$f_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
together with an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-term
$\mathcal{L}_{\textrm{PV}_k}$
-term
![]() $g(\bar{x}, y, w_0, \ldots, w_{m})$
such that all the following are provable in
$g(\bar{x}, y, w_0, \ldots, w_{m})$
such that all the following are provable in
![]() $\textrm{PV}_k$
:
$\textrm{PV}_k$
:
-
•
 $\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [f_i(\bar{x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar{x})]$
, for any
$\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [f_i(\bar{x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar{x})]$
, for any
 $0 \leq i \leq m$
.
$0 \leq i \leq m$
. -
•
 $\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [g(\bar{x}, y, w_0, \ldots, w_{m}) \leq t(\bar{x})]$
.
$\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [g(\bar{x}, y, w_0, \ldots, w_{m}) \leq t(\bar{x})]$
. -
•
 $ \forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w_0, \ldots, w_{m})) \to \bar{H}(\bar{x}, y, w_0, \ldots, w_m)]$
, where the formula
$ \forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w_0, \ldots, w_{m})) \to \bar{H}(\bar{x}, y, w_0, \ldots, w_m)]$
, where the formula
 $\bar{H}(\bar{x}, y, w_0, \ldots, w_m)$
is
$\bar{H}(\bar{x}, y, w_0, \ldots, w_m)$
is
 $\bigvee _{i=0}^m H(\bar{x}, f_i(\bar{x}, y, w_0, \ldots, w_{i-1}), w_i)$
.
$\bigvee _{i=0}^m H(\bar{x}, f_i(\bar{x}, y, w_0, \ldots, w_{i-1}), w_i)$
.
Remark 35. Here is a computational interpretation of a
![]() $(k, 2)$
-reduction as a nondeterministic version of the deterministic
$(k, 2)$
-reduction as a nondeterministic version of the deterministic
![]() $(k,2)$
-reductions we had before. A
$(k,2)$
-reductions we had before. A
![]() $(k, 2)$
-reduction starts with reading the first move
$(k, 2)$
-reduction starts with reading the first move
![]() $y \leq t(\bar{x})$
in
$y \leq t(\bar{x})$
in
![]() $(G, t)$
and uses
$(G, t)$
and uses
![]() $f_0$
to transform it to a first move
$f_0$
to transform it to a first move
![]() $v_0 \leq s(\bar{x})$
in
$v_0 \leq s(\bar{x})$
in
![]() $(H, s)$
. Then, as before it reads the second move
$(H, s)$
. Then, as before it reads the second move
![]() $w_0 \leq s(\bar{x})$
in
$w_0 \leq s(\bar{x})$
in
![]() $(H, s)$
. However, instead of using it to find a second move in
$(H, s)$
. However, instead of using it to find a second move in
![]() $(G, t)$
, it uses
$(G, t)$
, it uses
![]() $f_1$
to come up with another possible first move
$f_1$
to come up with another possible first move
![]() $v_1 \leq s(\bar{x})$
in
$v_1 \leq s(\bar{x})$
in
![]() $(H, s)$
and asks about its second move
$(H, s)$
and asks about its second move
![]() $w_1$
. It keeps repeating this procedure to finally after
$w_1$
. It keeps repeating this procedure to finally after
![]() $m+1$
many enquiries, it uses
$m+1$
many enquiries, it uses
![]() $g$
to compute the second move in
$g$
to compute the second move in
![]() $(G, t)$
. These computations are in a way that if the produced play for
$(G, t)$
. These computations are in a way that if the produced play for
![]() $(G, t)$
is winning, then one of the produced plays for
$(G, t)$
is winning, then one of the produced plays for
![]() $(H, s)$
is winning.
$(H, s)$
is winning.
The following theorem slightly modifies Herbrand’s theorem, Theorem 2, to connect the
![]() $\textrm{PV}_k$
-provability of the implication between the existence of the strategies and the existence of
$\textrm{PV}_k$
-provability of the implication between the existence of the strategies and the existence of
![]() $(k, 2)$
-reductions.
$(k, 2)$
-reductions.
Theorem.
Let
![]() $(G(\bar{x}, y, z), t(\bar{x}))$
and
$(G(\bar{x}, y, z), t(\bar{x}))$
and
![]() $(H(\bar{x}, v, w), s(\bar{x}))$
be two
$(H(\bar{x}, v, w), s(\bar{x}))$
be two
![]() $(k, 2)$
-games. Then
$(k, 2)$
-games. Then
iff there exists a
![]() $(k, 2)$
-reduction from
$(k, 2)$
-reduction from
![]() $(H, s)$
to
$(H, s)$
to
![]() $(G, t)$
.
$(G, t)$
.
Proof. One direction is clear. For the other, assume
Define
![]() $\tilde{G}(\bar{x}, y, z)$
as
$\tilde{G}(\bar{x}, y, z)$
as
![]() $[y \leq t(\bar{x}) \wedge (z \leq t(\bar{x}) \to G(\bar{x}, y, z))]$
and
$[y \leq t(\bar{x}) \wedge (z \leq t(\bar{x}) \to G(\bar{x}, y, z))]$
and
![]() $\tilde{H}(\bar{x}, v, w)$
as
$\tilde{H}(\bar{x}, v, w)$
as
![]() $[v \leq s(\bar{x}) \wedge (w \leq s(\bar{x}) \to H(\bar{x}, v, w))]$
. Now, by moving the quantifiers, we have
$[v \leq s(\bar{x}) \wedge (w \leq s(\bar{x}) \to H(\bar{x}, v, w))]$
. Now, by moving the quantifiers, we have
Using the pairing function available in
![]() $\textrm{PV}$
, we can make two variables
$\textrm{PV}$
, we can make two variables
![]() $v$
and
$v$
and
![]() $z$
into one variable, apply Herbrand’s theorem, Theorem 2 and then retrieve
$z$
into one variable, apply Herbrand’s theorem, Theorem 2 and then retrieve
![]() $y$
and
$y$
and
![]() $z$
again, by projections. Therefore, there are
$z$
again, by projections. Therefore, there are
![]() $\mathcal{L}_{\textrm{PV}_k}$
-terms
$\mathcal{L}_{\textrm{PV}_k}$
-terms
![]() $g_0(\bar{x}, y)$
,
$g_0(\bar{x}, y)$
,
![]() $h_0(\bar{x}, y)$
,
$h_0(\bar{x}, y)$
,
![]() $g_1(\bar{x}, y, w_0)$
,
$g_1(\bar{x}, y, w_0)$
,
![]() $h_1(\bar{x}, y, w_0)$
, …,
$h_1(\bar{x}, y, w_0)$
, …,
![]() $g_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
and
$g_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
and
![]() $h_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
such that
$h_m(\bar{x}, y, w_0, \ldots, w_{m-1})$
such that
Define
![]() $g'(\bar{x}, y, w_0, \ldots, w_{m})$
by cases: if
$g'(\bar{x}, y, w_0, \ldots, w_{m})$
by cases: if
![]() $\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
is false, define
$\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
is false, define
![]() $g'$
as
$g'$
as
![]() $g_0(\bar{x}, y)$
; if
$g_0(\bar{x}, y)$
; if
![]() $\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
is true but
$\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
is true but
![]() $\tilde{G}(\bar{x}, y, g_1(\bar{x}, y, w_0))$
is false, define
$\tilde{G}(\bar{x}, y, g_1(\bar{x}, y, w_0))$
is false, define
![]() $g'$
as
$g'$
as
![]() $g_1(\bar{x}, y, w_0)$
; if both
$g_1(\bar{x}, y, w_0)$
; if both
![]() $\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
and
$\tilde{G}(\bar{x}, y, g_0(\bar{x}, y))$
and
![]() $\tilde{G}(\bar{x}, y, g_1(\bar{x}, y, w_0))$
are true but
$\tilde{G}(\bar{x}, y, g_1(\bar{x}, y, w_0))$
are true but
![]() $\tilde{G}(\bar{x}, y, g_2(\bar{x}, y, w_0, w_1))$
is false, define
$\tilde{G}(\bar{x}, y, g_2(\bar{x}, y, w_0, w_1))$
is false, define
![]() $g'$
as
$g'$
as
![]() $g_2(\bar{x}, y, w_0, w_1)$
and so on. Finally, if all of
$g_2(\bar{x}, y, w_0, w_1)$
and so on. Finally, if all of
![]() $G(\bar{x}, y, g_i(\bar{x}, y, w_0, \ldots, w_{i-1}))$
’s are true, define
$G(\bar{x}, y, g_i(\bar{x}, y, w_0, \ldots, w_{i-1}))$
’s are true, define
![]() $g'$
as
$g'$
as
![]() $0$
:
$0$
:
 \begin{equation*} g'(\bar {x}, y, w_0, \ldots, w_{m})= \begin {cases} g_0(\bar {x}, y) & \neg \tilde {G}(\bar {x}, y, g_0(\bar {x}, y))\\ g_1(\bar {x}, y, w_0) & \tilde {G}(\bar {x}, y, g_0(\bar {x}, y)), \neg \tilde {G}(\bar {x}, y, g_1(\bar {x}, y, w_0))\\ $\ldots $ & $\ldots $\\ 0 & o.w. \end {cases} \end{equation*}
\begin{equation*} g'(\bar {x}, y, w_0, \ldots, w_{m})= \begin {cases} g_0(\bar {x}, y) & \neg \tilde {G}(\bar {x}, y, g_0(\bar {x}, y))\\ g_1(\bar {x}, y, w_0) & \tilde {G}(\bar {x}, y, g_0(\bar {x}, y)), \neg \tilde {G}(\bar {x}, y, g_1(\bar {x}, y, w_0))\\ $\ldots $ & $\ldots $\\ 0 & o.w. \end {cases} \end{equation*}
Note that
![]() $g'$
is defined in a way that unless
$g'$
is defined in a way that unless
![]() $\bigwedge _{i=0}^{m} \tilde{G}(\bar{x}, y, g_i(\bar{x}, y, w_0, \ldots, w_{i-1}))$
is true, we always have
$\bigwedge _{i=0}^{m} \tilde{G}(\bar{x}, y, g_i(\bar{x}, y, w_0, \ldots, w_{i-1}))$
is true, we always have
![]() $\neg \tilde{G}(\bar{x}, y, g'(\bar{x}, y, w_0, \ldots, w_{m}))$
. Therefore, it is easy to see that
$\neg \tilde{G}(\bar{x}, y, g'(\bar{x}, y, w_0, \ldots, w_{m}))$
. Therefore, it is easy to see that
and hence
Define
 \begin{equation*} f_i(\bar {x}, y, w_0, \ldots, w_{i-1})= \begin {cases} h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) & h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar {x})\\ 0 & h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) \gt s(\bar {x}) \end {cases} \end{equation*}
\begin{equation*} f_i(\bar {x}, y, w_0, \ldots, w_{i-1})= \begin {cases} h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) & h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar {x})\\ 0 & h_i(\bar {x}, y, w_0, \ldots, w_{i-1}) \gt s(\bar {x}) \end {cases} \end{equation*}
for any
![]() $0 \leq i \leq m$
and set
$0 \leq i \leq m$
and set
 \begin{equation*} g(\bar {x}, y, w_0, \ldots, w_{m})= \begin {cases} g'(\bar {x}, y, w_0, \ldots, w_{m}) & g'(\bar {x}, y, w_0, \ldots, w_{m}) \leq t(\bar {x})\\ 0 & g'(\bar {x}, y, w_0, \ldots, w_{m}) \gt t(\bar {x}) \end {cases} \end{equation*}
\begin{equation*} g(\bar {x}, y, w_0, \ldots, w_{m})= \begin {cases} g'(\bar {x}, y, w_0, \ldots, w_{m}) & g'(\bar {x}, y, w_0, \ldots, w_{m}) \leq t(\bar {x})\\ 0 & g'(\bar {x}, y, w_0, \ldots, w_{m}) \gt t(\bar {x}) \end {cases} \end{equation*}
It is clear that
![]() $\textrm{PV}_k \vdash f_i(\bar{x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar{x})$
, for any
$\textrm{PV}_k \vdash f_i(\bar{x}, y, w_0, \ldots, w_{i-1}) \leq s(\bar{x})$
, for any
![]() $0 \leq i \leq m$
and
$0 \leq i \leq m$
and
![]() $\textrm{PV}_k \vdash g(\bar{x}, y, w_0, \ldots, w_{m}) \leq t(\bar{x})$
. It is also clear that
$\textrm{PV}_k \vdash g(\bar{x}, y, w_0, \ldots, w_{m}) \leq t(\bar{x})$
. It is also clear that
and
are provable in
![]() $\textrm{PV}_k$
. Therefore, we reach the implication
$\textrm{PV}_k$
. Therefore, we reach the implication
![]() $\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w_0, \ldots, w_{m})) \to \bigvee _{i=0}^m H(\bar{x}, f_i(\bar{x}, y, w_0, \ldots, w_{i-1}), w_i)]$
in
$\forall \bar{w} \leq s(\bar{x}) \forall y \leq t(\bar{x}) [G(\bar{x}, y, g(\bar{x}, y, w_0, \ldots, w_{m})) \to \bigvee _{i=0}^m H(\bar{x}, f_i(\bar{x}, y, w_0, \ldots, w_{i-1}), w_i)]$
in
![]() $\textrm{PV}_k$
.
$\textrm{PV}_k$
.
Definition 36.
Let
![]() $k \geq 2$
be a natural number,
$k \geq 2$
be a natural number,
![]() $A(\bar{x}, y, z) \in \hat{\Sigma }^b_{k-1}$
be an
$A(\bar{x}, y, z) \in \hat{\Sigma }^b_{k-1}$
be an
![]() $\mathcal{L}_{\textrm{PV}_k}$
-formula and
$\mathcal{L}_{\textrm{PV}_k}$
-formula and
![]() $t(\bar{x})$
and
$t(\bar{x})$
and
![]() $r(\bar{x})$
be two
$r(\bar{x})$
be two
![]() $\mathcal{L}_{\textrm{PV}}$
-terms. By a
$\mathcal{L}_{\textrm{PV}}$
-terms. By a
![]() $\textrm{PLS}_{(k,2)}$
-program for the pair
$\textrm{PLS}_{(k,2)}$
-program for the pair
![]() $(A(\bar{x}, y, z), r(\bar{x}))$
, we mean a
$(A(\bar{x}, y, z), r(\bar{x}))$
, we mean a
![]() $(k, 2)$
-game
$(k, 2)$
-game
![]() $(G(\bar{x}, u, v, w), s(\bar{x}))$
(read
$(G(\bar{x}, u, v, w), s(\bar{x}))$
(read
![]() $u$
as a parameter) and
$u$
as a parameter) and
-
• an initial sequence
 $i(\bar{x}, w)$
of
$i(\bar{x}, w)$
of
 $\mathcal{L}_{\textrm{PV}_k}$
-terms as a
$\mathcal{L}_{\textrm{PV}_k}$
-terms as a
 $(k, 2)$
-reduction from the game
$(k, 2)$
-reduction from the game
 $(G(\bar{x}, 0, v, w), s(\bar{x}))$
to
$(G(\bar{x}, 0, v, w), s(\bar{x}))$
to
 $(\top, s(\bar{x}))$
,
$(\top, s(\bar{x}))$
, -
• a sequence
 $N(\bar{x}, u, v, w)$
of
$N(\bar{x}, u, v, w)$
of
 $\mathcal{L}_{\textrm{PV}_k}$
-terms as a
$\mathcal{L}_{\textrm{PV}_k}$
-terms as a
 $(k, 2)$
-reduction from the game
$(k, 2)$
-reduction from the game
 $(G(\bar{x}, u+1, v, w), s(\bar{x}))$
to
$(G(\bar{x}, u+1, v, w), s(\bar{x}))$
to
 $(G(\bar{x}, u, v, w), s(\bar{x}))$
,
$(G(\bar{x}, u, v, w), s(\bar{x}))$
, -
• a sequence
 $p(\bar{x}, v, z)$
of
$p(\bar{x}, v, z)$
of
 $\mathcal{L}_{\textrm{PV}_k}$
-terms as a
$\mathcal{L}_{\textrm{PV}_k}$
-terms as a
 $(k, 2)$
-reduction from the game
$(k, 2)$
-reduction from the game
 $(A(\bar{x}, y, z), r(\bar{x}))$
to
$(A(\bar{x}, y, z), r(\bar{x}))$
to
 $(G(\bar{x}, t(\bar{x}), v, w), s(\bar{x}))$
. Here, we pretend that
$(G(\bar{x}, t(\bar{x}), v, w), s(\bar{x}))$
. Here, we pretend that
 $A(\bar{x}, y, z)$
is a quantifier-free
$A(\bar{x}, y, z)$
is a quantifier-free
 $\mathcal{L}_{\textrm{PV}_k}$
-formula.
$\mathcal{L}_{\textrm{PV}_k}$
-formula.
By
![]() $\textrm{PLS}_{(k, 2)}$
, we mean the class of all the pairs
$\textrm{PLS}_{(k, 2)}$
, we mean the class of all the pairs
![]() $(A(\bar{x}, y, z), r(\bar{x}))$
for which there exists a
$(A(\bar{x}, y, z), r(\bar{x}))$
for which there exists a
![]() $\textrm{PLS}_{(k, 2)}$
-program. By
$\textrm{PLS}_{(k, 2)}$
-program. By
![]() $\textrm{PLS}_{(k, 2)}^p$
, we mean the class of all the pairs
$\textrm{PLS}_{(k, 2)}^p$
, we mean the class of all the pairs
![]() $(A(\bar{x}, y, z), r(\bar{x}))$
for which there exists a
$(A(\bar{x}, y, z), r(\bar{x}))$
for which there exists a
![]() $\textrm{PLS}_{(k, 2)}$
-program with polynomial length, that is,
$\textrm{PLS}_{(k, 2)}$
-program with polynomial length, that is,
![]() $t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
$t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
![]() $q$
.
$q$
.
One can read a (polynomial)
![]() $\textrm{PLS}_{(k, 2)}$
-program as (a polynomially) an exponentially long sequence of reductions between
$\textrm{PLS}_{(k, 2)}$
-program as (a polynomially) an exponentially long sequence of reductions between
![]() $2$
-turn games, starting with an explicit winning strategy for the first game, where all the functions and predicates live in the
$2$
-turn games, starting with an explicit winning strategy for the first game, where all the functions and predicates live in the
![]() $k$
-th level of the polynomial hierarchy verified in
$k$
-th level of the polynomial hierarchy verified in
![]() $\textrm{PV}_k$
.
$\textrm{PV}_k$
.
Similar to what we had in the last subsubsection, we can finally witness provability in
![]() $T^k_2$
(resp.
$T^k_2$
(resp.
![]() $S^k_2$
) by (resp. polynomial)
$S^k_2$
) by (resp. polynomial)
![]() $\textrm{PLS}_{(k, 2)}$
-programs.
$\textrm{PLS}_{(k, 2)}$
-programs.
Corollary 37.
Let
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $A(\bar{x}, y, z) \in \hat{\Sigma }^b_{k-2}$
and
$A(\bar{x}, y, z) \in \hat{\Sigma }^b_{k-2}$
and
![]() $r(\bar{x})$
be an
$r(\bar{x})$
be an
![]() $\mathcal{L}_{\textrm{PV}}$
-term:
$\mathcal{L}_{\textrm{PV}}$
-term:
-
(i)
 $S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(x) A(\bar{x}, y, z)$
iff
$S^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(x) A(\bar{x}, y, z)$
iff
 $(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}^p_{(k-1, 2)}$
.
$(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}^p_{(k-1, 2)}$
. -
(ii)
 $T^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
iff
$T^{k}_2 \vdash \forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
iff
 $(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}_{(k-1,2)}$
.
$(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}_{(k-1,2)}$
.
Proof.
The proof is similar to that of Corollary 30. Therefore, we only explain the main ingredients for
![]() $(i)$
. For the right to left, assume that there is a
$(i)$
. For the right to left, assume that there is a
![]() $\textrm{PLS}_{(k, 2)}$
-program for
$\textrm{PLS}_{(k, 2)}$
-program for
![]() $(A(\bar{x}, y, z), r(\bar{x}))$
with the length
$(A(\bar{x}, y, z), r(\bar{x}))$
with the length
![]() $q(|\bar{x}|)$
, for some polynomial
$q(|\bar{x}|)$
, for some polynomial
![]() $q$
. We use Theorem 8 to transform the existence of the reductions in the
$q$
. We use Theorem 8 to transform the existence of the reductions in the
![]() $\textrm{PLS}_{(k, 2)}$
-program to the following provable implications:
$\textrm{PLS}_{(k, 2)}$
-program to the following provable implications:
-
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, 0, v, w)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, 0, v, w)$
. -
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \rightarrow \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u+1, v, w)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \rightarrow \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u+1, v, w)$
. -
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), v, w) \to \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), v, w) \to \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
.
As any quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_{k-1}}$
-formula can be interpreted as an
$\mathcal{L}_{\textrm{PV}_{k-1}}$
-formula can be interpreted as an
![]() $\mathcal{L}_{\textrm{PV}}$
-formula in
$\mathcal{L}_{\textrm{PV}}$
-formula in
![]() $\hat{\Pi }^b_{k-1}$
and
$\hat{\Pi }^b_{k-1}$
and
![]() $\textrm{PV}_{k-1}$
can be interpreted in
$\textrm{PV}_{k-1}$
can be interpreted in
![]() $S^{k-1}_2$
, we can pretend that all the above implications are provable in
$S^{k-1}_2$
, we can pretend that all the above implications are provable in
![]() $S^k_2$
and
$S^k_2$
and
![]() $G \in \hat{\Pi }^b_{k-1}$
. Therefore, we can assume that
$G \in \hat{\Pi }^b_{k-1}$
. Therefore, we can assume that
![]() $\exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \in \hat{\Sigma }^b_k$
. Using
$\exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \in \hat{\Sigma }^b_k$
. Using
![]() $\textrm{LInd}$
in
$\textrm{LInd}$
in
![]() $S^k_2$
on the formula
$S^k_2$
on the formula
![]() $\exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w)$
, we reach
$\exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w)$
, we reach
![]() $S^k_2 \vdash \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
. Conversely, we assume that
$S^k_2 \vdash \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
. Conversely, we assume that
![]() $S^k_2 \vdash \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
. Hence,
$S^k_2 \vdash \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
. Hence,
![]() $\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z) \to \bot$
is provable in
$\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z) \to \bot$
is provable in
![]() $S^k_2$
. Since
$S^k_2$
. Since
![]() $A \in \hat{\Sigma }^b_{k-2}$
, the formula
$A \in \hat{\Sigma }^b_{k-2}$
, the formula
![]() $\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z)$
is in
$\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z)$
is in
![]() $\hat{\Pi }^b_{k}$
. Hence, by Theorem 6, we have
$\hat{\Pi }^b_{k}$
. Hence, by Theorem 6, we have
![]() $\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z) \rhd ^p_k \bot$
. Call the
$\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \neg A(\bar{x}, y, z) \rhd ^p_k \bot$
. Call the
![]() $k$
-flow
$k$
-flow
![]() $(H(u, \bar{x}), t(\bar{x}))$
, where
$(H(u, \bar{x}), t(\bar{x}))$
, where
![]() $t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
$t(\bar{x})=q(|\bar{x}|)$
, for some polynomial
![]() $q$
. Without loss of generality, write
$q$
. Without loss of generality, write
![]() $H(u, \bar{x})$
in the form
$H(u, \bar{x})$
in the form
![]() $\forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u, v, w)$
, where
$\forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u, v, w)$
, where
![]() $J \in \hat{\Pi }^b_{k-2}$
. As
$J \in \hat{\Pi }^b_{k-2}$
. As
![]() $k \geq 2$
, the theory
$k \geq 2$
, the theory
![]() $\textrm{PV}$
is a subtheory of
$\textrm{PV}$
is a subtheory of
![]() $\textrm{PV}_{k-1}$
. Therefore, moving the implications in the definition of the
$\textrm{PV}_{k-1}$
. Therefore, moving the implications in the definition of the
![]() $k$
-flow from
$k$
-flow from
![]() $\textrm{PV}$
to
$\textrm{PV}$
to
![]() $\textrm{PV}_{k-1}$
, we have:
$\textrm{PV}_{k-1}$
, we have:
-
•
 $\textrm{PV}_{k-1} \vdash [\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \; \neg A(\bar{x}, y, z)] \to \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, 0, v, w)$
.
$\textrm{PV}_{k-1} \vdash [\forall y \leq r(\bar{x}) \exists z \leq r(\bar{x}) \; \neg A(\bar{x}, y, z)] \to \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, 0, v, w)$
. -
•
 $\textrm{PV}_{k-1} \vdash \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, q(|\bar{x}|), v, w) \to \bot$
.
$\textrm{PV}_{k-1} \vdash \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, q(|\bar{x}|), v, w) \to \bot$
. -
•
 $\textrm{PV}_{k-1} \vdash \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u, v, w) \rightarrow \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u+1, v, w)$
.
$\textrm{PV}_{k-1} \vdash \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u, v, w) \rightarrow \forall v \leq s(\bar{x}) \exists w \leq s(\bar{x}) J(\bar{x}, u+1, v, w)$
.
As
![]() $J \in \hat{\Pi }^b_{k-2}$
, in
$J \in \hat{\Pi }^b_{k-2}$
, in
![]() $\textrm{PV}_{k-1}$
, we can pretend that
$\textrm{PV}_{k-1}$
, we can pretend that
![]() $J$
is a quantifier-free
$J$
is a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}_{k-1}}$
-formula. Define
$\mathcal{L}_{\textrm{PV}_{k-1}}$
-formula. Define
![]() $G(\bar{x}, u, v, w)$
as
$G(\bar{x}, u, v, w)$
as
![]() $\neg J(\bar{x}, q(|\bar{x}|) \dot{-} u, v, w)$
. Therefore, we have:
$\neg J(\bar{x}, q(|\bar{x}|) \dot{-} u, v, w)$
. Therefore, we have:
-
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), v, w) \to \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, q(|\bar{x}|), v, w) \to \exists y \leq r(\bar{x}) \forall z \leq r(\bar{x}) A(\bar{x}, y, z)$
. -
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, 0, v, w)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, 0, v, w)$
. -
•
 $\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \rightarrow \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u+1, v, w)$
.
$\textrm{PV}_{k-1} \vdash \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u, v, w) \rightarrow \exists v \leq s(\bar{x}) \forall w \leq s(\bar{x}) G(\bar{x}, u+1, v, w)$
.
Finally, it is enough to use Theorem 8 to get a
![]() $\textrm{PLS}_{(k-1, 2)}$
-program for the pair
$\textrm{PLS}_{(k-1, 2)}$
-program for the pair
![]() $(A(\bar{x}, y, z), r(\bar{x}))$
with the length
$(A(\bar{x}, y, z), r(\bar{x}))$
with the length
![]() $q(|\bar{x}|)$
. Hence,
$q(|\bar{x}|)$
. Hence,
![]() $(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}^p_{(k-1, 2)}$
.
$(A(\bar{x}, y, z), r(\bar{x})) \in \textrm{PLS}^p_{(k-1, 2)}$
.
It is worth putting Corollary 37 for the concrete case
![]() $k=2$
into plain words. Here, the corollary characterizes the
$k=2$
into plain words. Here, the corollary characterizes the
![]() $T^2_2$
-provability (resp.
$T^2_2$
-provability (resp.
![]() $S^2_2$
-provability) of a formula in the form
$S^2_2$
-provability) of a formula in the form
![]() $\forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(x) A(\bar{x}, y, z)$
, where
$\forall \bar{x} \exists y \leq r(\bar{x}) \forall z \leq r(x) A(\bar{x}, y, z)$
, where
![]() $A$
is a polynomial time computable predicate represented as a quantifier-free
$A$
is a polynomial time computable predicate represented as a quantifier-free
![]() $\mathcal{L}_{\textrm{PV}}$
-formula by the existence of an exponentially (resp. polynomially) long sequence of polynomial time reductions between polynomial time games starting on an explicit polynomial time winning strategy in the first game.
$\mathcal{L}_{\textrm{PV}}$
-formula by the existence of an exponentially (resp. polynomially) long sequence of polynomial time reductions between polynomial time games starting on an explicit polynomial time winning strategy in the first game.
Acknowledgements
We are grateful to Pavel Pudlák and Neil Thapen for the fruitful discussions we had and for bringing the connection between the total search problems and the theories of arithmetic into our attention. We are also thankful to the anonymous referees whose suggestions improved the paper’s presentation. The support by the FWF project P 33548 and the Czech Academy of Sciences (RVO 67985840) is also gratefully acknowledged.