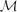Contents
Introduction
Introduction: special issue ICICTA 2012
-
- Published online by Cambridge University Press:
- 04 September 2014, e240501
-
- Article
- Export citation
Editorial Preface
Preface to the special issue on developments of the concepts of randomness, statistics and probability
-
- Published online by Cambridge University Press:
- 28 March 2014, e240301
-
- Article
-
- You have access
- Export citation
Foreword
Foreword: special issue on structure transformation
-
- Published online by Cambridge University Press:
- 26 June 2014, 240401
-
- Article
-
- You have access
- Export citation
Paper
An operational domain-theoretic treatment of recursive types†
-
- Published online by Cambridge University Press:
- 19 March 2013, e240101
-
- Article
- Export citation
Interactive Realizability for second-order Heyting arithmetic with EM1 and SK1
-
- Published online by Cambridge University Press:
- 25 October 2013, e240601
-
- Article
- Export citation
Computability structures, simulations and realizability
-
- Published online by Cambridge University Press:
- 05 June 2013, e240201
-
- Article
- Export citation
Fixed points of contractive maps on dcpo's
-
- Published online by Cambridge University Press:
- 13 May 2013, e240102
-
- Article
- Export citation
Processes and unfoldings: concurrent computations in adhesive categories
-
- Published online by Cambridge University Press:
- 26 June 2014, 240402
-
- Article
- Export citation
Trace spaces of directed tori with rectangular holes
-
- Published online by Cambridge University Press:
- 17 June 2013, e240202
-
- Article
- Export citation
Kolmogorov on the role of randomness in probability theory
-
- Published online by Cambridge University Press:
- 28 March 2014, e240302
-
- Article
- Export citation
Database queries and constraints via lifting problems
-
- Published online by Cambridge University Press:
- 11 October 2013, e240602
-
- Article
- Export citation
A cooperative co-evolutionary particle swarm optimiser based on a niche sharing scheme for the flow shop scheduling problem under uncertainty
-
- Published online by Cambridge University Press:
- 04 September 2014, e240502
-
- Article
- Export citation
Equivalence relations for modular performance evaluation in dtsPBC
-
- Published online by Cambridge University Press:
- 14 May 2013, e240103
-
- Article
- Export citation
Finitary
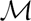 $\mathcal{M}$-adhesive categories
$\mathcal{M}$-adhesive categories
-
- Published online by Cambridge University Press:
- 26 June 2014, 240403
-
- Article
- Export citation
Higher-order psi-calculi†
-
- Published online by Cambridge University Press:
- 24 June 2013, e240203
-
- Article
- Export citation
A quantum random number generator certified by value indefiniteness
-
- Published online by Cambridge University Press:
- 28 March 2014, e240303
-
- Article
- Export citation
A hybrid WT-FBPNN optimisation algorithm to identify the investment risk of wind power projects†
-
- Published online by Cambridge University Press:
- 04 September 2014, e240503
-
- Article
- Export citation
Realizability interpretation of PA by iterated limiting PCA
-
- Published online by Cambridge University Press:
- 11 March 2014, e240603
-
- Article
- Export citation
Event Identifier Logic†
-
- Published online by Cambridge University Press:
- 27 September 2013, e240204
-
- Article
- Export citation
A linear category of polynomial diagrams
-
- Published online by Cambridge University Press:
- 17 May 2013, e240104
-
- Article
- Export citation