If E1 and E2 are subsets of ℝn and a- is an isometry or similarity transformation, it is useful to be able to estimate the Hausdorff dimension of E1 ∩ σ(E2) in terms of the dimensions of E1 and E2. If E1 and E2 are compact, then, as σvaries, dim (El ∩ σ(E2)) is “in general” at most max (dim E1 + dim E2 − n, 0) and “often” at least this value (see Mattila [9] and Kahane [7] for more precise statements of these ideas). However, as we shall see, it is possible to construct non-compact sets E of any given dimension that are “sufficiently dense” in ℝn to ensure that dim (E ∩ σ(E)) = dim E for all similarities σ More generally, we shall show that for each s there are large classes of sets & of dimensions between s and n, closed under reasonable transformations including similarities, such that the intersection of any countable collection of sets in & has dimension at least s. Such collections of sets are required, for example, in the constructions of subsets of ℝn with certain dimensional properties given by Davies [1] and Falconer [5].

If E is a subset of ℝn (n ≥ 1) we define the distance set of E as

The best known result on distance sets is due to Steinhaus [11], namely, that, if E ⊂ ℝn is measurable with positive n-dimensional Lebesgue measure, then D(E) contains an interval [0, ε) for some ε > 0. A number of variations of this have been examined, see Falconer [6, p. 108] and the references cited therein.

Let A and B be Borel (or more generally Suslin) sets in ℝn whose Hausdorff dimensions satisfy

Le point de départ de ce travail est le résultat suivant.

THÉORÈME (I. Namioka). Soient X et Y deux espaces compacts et

Si f est continue quand on munit(Y) de la topologie de convergence simple alors X contient un Gδ dense en tout point duquel f reste continue quand on munit(Y) de la topologie de la convergence uniform.

In [8,9] Jayne and Rogers studied piece-wise closed maps and ℱσ maps between metric spaces. A map f of a metric space X into a metric space Y is said to be an ℱσ map if: (a) f maps ℱσ-sets in X to ℱσ-sets in Y; and (b) f1 maps ℱσ-sets in Y back to ℱσ-sets in X. A map fof a metric space X into a metric space Y is said to be piece-wise closed if:it is possible to find a sequence X1, X2,… of closed sets in X, with with each setf(Xi), i ≥ 1, closed in Y, and with the restriction offto each Xi, a closed map (i.e., a continuous map that maps closed sets to closed sets).

Let be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point z0 in Δ we can evaluate all matrix entries of at z0, to obtain a subgroup {z0} of SL (2, ℂ) and a surjective representation → {z0}. If this representation is not faithful, then contains a nontrivial element W such that W evaluated; at z0 is trivial. But W can evaluate to the identity only on a countable subset) of Δ, and there are only countably many choices for W in Consequently there are at most countably many points zk in Δ such that {zk} is not isomorphic to Δ. Our main result can now be stated as follows.

We use the Buchstab-Rosser sieve to derive an asymptotic formula for the distribution of those integers n for which the r numbers n + l1, n + l2,…, n + lr are all square-free. Our error estimate sharpens a similar result of Hall and is uniform in both r and maxl 1≤i≤r|li|.

The work to be described here, with the fruit of previous investigations in [1] and [2], yields the following general theorem.

We consider two additive cubic equations

in p-adic fields. Davenport and Lewis showed that the equations have a non-trivial solution in every p-adic field, if n ≥ 16, and need not have a solution in the 7-adic field, if n = 15. Here we prove that if p ≠ 7 the equations have a non-trivial solution in p-adic fields if n ≥ 13. When n = 12 such a result fails for every prime p ≡ 1 (mod 3).

Suppose that θ is a positive irrational number and α is an arbitrary real number. Then Kronecker's Theorem in diophantine approximation (Theorem 440 of [7[) can be stated as follows.

In 1959 C. A. Rogers gave the following estimate for the density ϑ(k) of lattice-coverings of euclidean d-space Ed with convex bodies 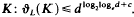. Here, c is a suitable constant which does not depend on d and K. Moreover, Rogers proved that for the unit ball Bd the upper bound can be replaced by 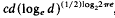, which is, of course a major improvement. In the present paper we show that such an improvement can be obtained for a larger class of convex bodies. In particular, we prove the following theorem. Let K be a convex body in Ed, and let k be an integer satisfying k > log2 loge d + 4. If there exist at least k hyperplanes H1,…, Hk with normals mutually perpendicular and an affine transformation A such that A(K) is symmetrical with respect to Hl,…,Hk, respectively, then 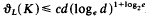. Actually, for a bound of this type we do not even need any symmetry assumption. In fact, some weaker properties concerning shadow boundaries will suffice.

For d, n positive integers, let α(d, n) be the statement “For every abelian variety A bounded by d there exists a point P of order n”. Let l1, l2, l3, … be the sequence of prime numbers and let α be

This paper considers the flow of a dissipative fluid in a radial bearing. By looking at the equations in the thermal boundary layer it is shown that, if a certain parameter m is less than unity, then the temperature in the boundary layer is bounded for all time.

In our paper [12[ we made extensive use of the details of the proofs given in our earlier paper [11], and, in particular, we claimed that Lemma 3 of [11] holds, not just when Y is a metric space, but also when Y is a Hausdorff space, provided X × Y is a Fréchet space. In a corrigendum to [11], we give a corrected version of this Lemma 3, but it seems to depend, in an essential way, on the assumption that Y is a metric space, or at least a perfectly normal space. In this note we show that a modified version of this Lemma 3 enables us to justify all the theorems in [12] by use of a modified method of selection.