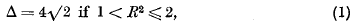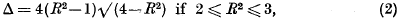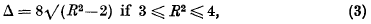Contents
Research Article
The stability of a rigidly rotating column of liquid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
On infinitesimal triangles
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-14
-
- Article
- Export citation
The discriminants of relative extensions and the existence of integral bases
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-22
-
- Article
- Export citation
Symmetrically loaded shallow shells of revolution
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-35
-
- Article
- Export citation
Distinct small values of quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-40
-
- Article
- Export citation
Incidence matrices
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-49
-
- Article
- Export citation
A combinatorial problem of T. G. Room
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-55
-
- Article
- Export citation
A mixed packing problem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-63
-
- Article
- Export citation
The flow of a conducting fluid past a magnetized cylinder
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-77
-
- Article
- Export citation
On Stokes flow about a torus
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-92
-
- Article
- Export citation
Front matter
MTK volume 7 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
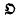 . We shall be concerned here with the structure of such rings
. We shall be concerned here with the structure of such rings