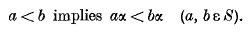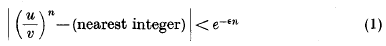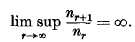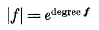Contents
Research Article
A note on coverings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
-
- Article
- Export citation
Cubic forms over algebraic number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-101
-
- Article
- Export citation
Homogeneous forms of odd degree in a large number of variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-105
-
- Article
- Export citation
Multiple covering of the plane by circles
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-16
-
- Article
- Export citation
Bounded representations of integers by quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
-
- Article
- Export citation
The distribution of quadratic residues and non-residues
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
-
- Article
- Export citation
A note on summability factors
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-40
-
- Article
- Export citation
On a method for the determination of class number factors in number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-121
-
- Article
- Export citation
Groups of order automorphisms of ordered sets
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-50
-
- Article
- Export citation
On the fractional parts of the powers of a rational number (II)
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
-
- Article
- Export citation
Rational approximations to algebraic numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-131
-
- Article
- Export citation
A note on form rings and ideals
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-60
-
- Article
- Export citation
The product of n linear forms in a field of series
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 132-137
-
- Article
- Export citation
The Green's function of an elliptic plate
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-69
-
- Article
- Export citation
Note on two theorems about function algebras
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-139
-
- Article
- Export citation
Uniqueness theorems for thin clamped anisotropic plates
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 70-75
-
- Article
- Export citation
On the expansion of functions satisfying four boundary conditions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-145
-
- Article
- Export citation
Stress distribution in a notched plate
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-96
-
- Article
- Export citation
An inversion formula for a generalized transform
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 146-155
-
- Article
- Export citation
Front matter
MTK volume 4 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
-
- Article
-
- You have access
- Export citation
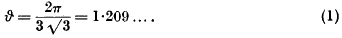

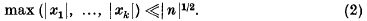
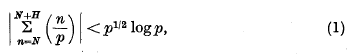
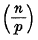 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.