Contents
Research Article
Equicontinuity on Harmonic Spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-6
-
- Article
-
- You have access
- Export citation
Some Results and Problems Concerning Chordal Principal Cluster Sets*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 7-18
-
- Article
-
- You have access
- Export citation
On a Theorem of Schwarz Type for Quasiconformal Mappings in Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 19-30
-
- Article
-
- You have access
- Export citation
On the Class Number of a Relatively Cyclic Number Field
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 31-44
-
- Article
-
- You have access
- Export citation
Note on the Uniqueness Proprety of Weak Solutions of Parabolic Equations
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 45-49
-
- Article
-
- You have access
- Export citation
Perfect Picard Set of Positive Capacity
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 51-56
-
- Article
-
- You have access
- Export citation
A Property of Weak Solutions for Some Parabolic Equations of Higher Order
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 57-60
-
- Article
-
- You have access
- Export citation
Sur les Fonctions Méromorphes aux Limites Fines
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-68
-
- Article
-
- You have access
- Export citation
PL-Submanifolds and Homology Classes of a PL-Manifold*)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 69-74
-
- Article
-
- You have access
- Export citation
Generalization of Levi-Oka’s Theorem Concerning Meromorphic Functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 75-84
-
- Article
-
- You have access
- Export citation
A Theorem on Valuation Rings and its Applications
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 85-91
-
- Article
-
- You have access
- Export citation
Sario’s Potentials and Analytic Mappings*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 93-101
-
- Article
-
- You have access
- Export citation
The Theorem of Identity for Coherent Analytic Modules
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 103-120
-
- Article
-
- You have access
- Export citation
On q-th Derivative of Vector Bundles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 121-126
-
- Article
-
- You have access
- Export citation
Finite Dimensional Approximations to Some Flows on the Projective Limit Space of Spheres II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 127-135
-
- Article
-
- You have access
- Export citation
Border Reduction in Existence Problems of Harmonic Forms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 137-143
-
- Article
-
- You have access
- Export citation
Singular Sets of Some Kleinian Groups (II)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-162
-
- Article
-
- You have access
- Export citation
Hyperbolic Motions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 163-166
-
- Article
-
- You have access
- Export citation
On the Zeros of Power Series with Hadamard Gaps
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 167-174
-
- Article
-
- You have access
- Export citation
Definitions for a Class of Plane Quasiconformal Mappings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 175-184
-
- Article
-
- You have access
- Export citation
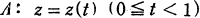 such that |
such that |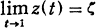 . A terminal subarc of an arc
. A terminal subarc of an arc 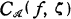 is the outer angular cluster set of
is the outer angular cluster set of 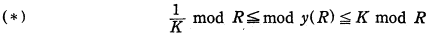
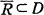 , where
, where 
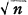 and
and 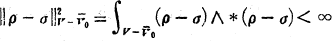 was given a complete solution in [2]. The corresponding problem for harmonic forms
was given a complete solution in [2]. The corresponding problem for harmonic forms 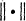 by the point norm [3].
by the point norm [3].
