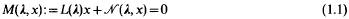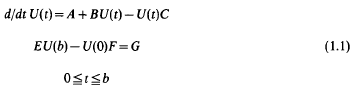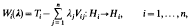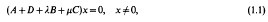Contents
Research Article
Unstable invariant distributions for a class of stochastic delay equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-23
-
- Article
-
- You have access
- Export citation
Microlocal regularity on step two nilpotent Lie groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 25-39
-
- Article
-
- You have access
- Export citation
Cohomology of induced modules in rings of differential operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-47
-
- Article
-
- You have access
- Export citation
Multiparameter spectral theory of singular differential operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-66
-
- Article
-
- You have access
- Export citation
A nonabelian Frobenius–Wielandt complement
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 67-69
-
- Article
-
- You have access
- Export citation
On the automorphisms of the group ring of a finitely generated free abelian group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 71-75
-
- Article
-
- You have access
- Export citation
Simple eigenvalues and bifurcation for a multiparameter problem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 77-88
-
- Article
-
- You have access
- Export citation
Hyperbolic travelling fronts
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 89-97
-
- Article
-
- You have access
- Export citation
An algorithm for solving generalized algebraic Lyapunov equations in Hilbert space, applications to boundary value problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 99-105
-
- Article
-
- You have access
- Export citation
Boundary value problem for a singularly perturbed system of linear differential equations with impulses
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-126
-
- Article
-
- You have access
- Export citation
Multiparameter spectral theory and Taylor's joint spectrum in Hilbert space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 127-144
-
- Article
-
- You have access
- Export citation
Covering lemmas revisited
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 145-150
-
- Article
-
- You have access
- Export citation
Inverse multiparameter eigenvalue problems for matrices III
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-155
-
- Article
-
- You have access
- Export citation
Asymptotic equivalence of a linear and nonlinear system with impulse effect
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 157-163
-
- Article
-
- You have access
- Export citation
Book Reviews
M. Aschbacher, Finite group theory (Cambridge studies in advanced mathematics 10, Cambridge University Press, 1986), ix + 274 pp., £22.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 165-166
-
- Article
-
- You have access
- Export citation
J. B. Conway, A course in functional analysis (Graduate Texts in Mathematics 96, Springer-Verlag, 1985), xiv + 404 pp. DM 118.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 166
-
- Article
-
- You have access
- Export citation
D. J. H. Garling, A course in Galois theory (Cambridge University Press, 1986), pp. 167, cloth £22.50, paper £8.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 166-167
-
- Article
-
- You have access
- Export citation
Hideyuki Matsumura, Commutative ring theory (Cambridge studies in advanced mathematics 8, Cambridge University Press, 1986), pp. 320, £30.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 167-168
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 31 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 31 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, p. b1
-
- Article
-
- You have access
- Export citation
 :
: