A mixed-order system of singular partial differential equations occurring in the study of rotating stars is considered. It is shown that the associated operator L0 is closable and that the essential spectrum of its closure L coincides with the essential spectrum of a bounded operator. Finally, some parts of the essential spectrum of L are determined explicitly.

We consider the Sturm–Liouville equationwith the initial conditionand suppose that Weyl's limit-point case holds at infinity. Let ρα(μ) be the corresponding spectral function and its symmetric derivative. We show that for almost all μ ∈ R, if exists and is positive for some α ∈ [0, π), then (i) exists and is positive for all β ∈ [0, π), and (ii) for all α1, α2 ∈ (0, π) \ {½ π},

We study the singularly perturbed problem —εαΔuε + uε = f (α > 0) with the Dirichlet boundary condition in a perforated domain, in which the holes are distributed periodically with period 2ε throughout a fixed domain Ω. The asymptotic behaviour of uε when ε → 0, together with corrector results and error estimates in L2(Ω), are deduced for all sizes of holes. The behaviour of uε in is obtained for the cases where the size of holes is of order ε or is of a sufficiently smaller order. When the holes' size is of a sufficiently small order, as expected, uε has similar behaviour to that in the case of a non-varying domain.

We show by elementary methods that there are symplectic embeddings from standard (R2n, ω0) into (Σ x R2n−2, ω ⊕ ω0) and (T2n−2k x R2k, ω ⊕ ω0), where (Σ, ω) is a closed two-dimensional symplectic manifold, and (T2n−2k, ω) is the torus with a constant symplectic form ω. Some estimates of Gromov's symplectic capacity are given for bounded domains in these manifolds.

In a previous paper, I investigated the use (for the inverse scattering problem) of the resonant frequencies and the associated eigen far-fields. I showed that the shape of a sound soft obstacle is uniquely determined by a knowledge of one resonant frequency and one associated eigen far-field. Inverse obstacle scattering problems are ill-posed in the sense that a small error in the measurement may imply a large error in the reconstruction. This is contrary to the idea of continuity. I proved that, by adding some a priori information, the reconstruction becomes continuous. More precisely, continuity holds if we assume that the obstacle lies a fixed and known compact set.

The goal of this paper is to extend these results to the case of absorbing obstacles.

We consider the following elliptic equation:where m > 0, f(x, u)/u tends to a positive constant as u → + ∞. Here, the nonlinear term f(x, u) does not satisfy the usual condition, that is, for some θ > 0,which is important in using the mountain pass theorem. The aim of this paper is to discuss how to use the mountain pass theorem to show the existence of a positive solution to the present problem when we lose the above condition. Furthermore, if f(x, u) ≡ f(u), we also prove that the above problem has a ground state by using the artificial constraint method.

The Stokes problem on a domain with edge singularities is considered. The decomposition of the solution into a regular part and blocks of singular functions is established. This, together with the tangential regularity of the solution, leads to a global regularity result in suitable weighted Sobolev spaces, the properties of which are investigated. The global regularity is exploited to generate an optimally convergent semi-discrete mesh refinement mixed finite-element method. In the particular case of a prismatic domain, the Fourier finite-element method, which is a fully discrete scheme, is implemented.

We are concerned with positive solutions decaying at infinity for a class of semilinear elliptic equations in all of RN having superlinear subcritical nonlinearity. The corresponding variational problem lacks compactness because of the unboundedness of the domain and, in particular, it cannot be solved by minimization methods. However, we prove the existence of a positive solution, corresponding to a higher critical value of the related functional, under a suitable fast decay condition on the coefficient of the linear term. Moreover, we analyse the behaviour of the solution as this coefficient goes to infinity and show that the solution tends to split as the sum of two positive functions sliding to infinity in opposite directions. Finally, we use this property to prove the existence of at least 2k − 1 distinct positive solutions, when this coefficient splits as the sum of k bumps sufficiently far apart.

In this paper, we study the non-existence of solutions for the following (model) problem in a bounded open subset Ω of RN: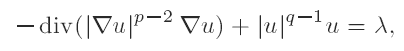with Dirichlet boundary conditions, where p > 1, q > 1 and μ is a bounded Radon measure. We prove that if λ is a measure which is concentrated on a set of zero r capacity (p < r ≤ N), and if q > r (p − 1)/(r − p), then there is no solution to the above problem, in the sense that if one approximates the measure λ with a sequence of regular functions fn, and if un is the sequence of solutions of the corresponding problems, then un converges to zero.

We also study the non-existence of solutions for the bilateral obstacle problem with datum a measure λ concentrated on a set of zero p capacity,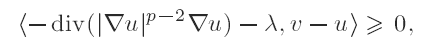with u in for every υ in K, finding again that the only solution obtained by approximation is u = 0.

We study some global geometric properties of a static Lorentzian manifold Λ embedded in a differentiable manifold M, with possibly non-smooth boundary ∂Λ. We prove a variational principle for geodesics in static manifolds, and using this principle we establish the existence of geodesics that do not touch ∂Λ and that join two fixed points of Λ. The results are obtained under a suitable completeness assumption for Λ that generalizes the property of global hyperbolicity, and a weak convexity assumption on ∂Λ. Moreover, under a non-triviality assumption on the topology of Λ, we also get a multiplicity result for geodesics in Λ joining two fixed points.

Given a bounded smooth domain Ω ⊂ Rn, n ≥ 2, and a second-order elliptic self-adjoint operator A on Ω, the set of points (α, β) ∈ R2 for which the problem Au = αu+ − βu- in Ω, u = 0 on ∂Ω (where u± = max{±u, 0}), has a non-trivial solution is called the Fucik spectrum of A. In this note we extend some recent results of Pistoia on the structure of this set for generic operators A (the genericity is with respect to the domain Ω or the coefficients of A).