In this paper I extend the analysis of regular problems containing the eigenvalue parameter in the boundary conditions given by Walter (1973) and myself (1977) to singular problems which involve the eigenvalue parameter linearly in a regular or a limit-circle boundary condition at the left endpoint. The formulation of the limit-circle boundary conditions follows that given in another paper by the present author in 1977, and has the advantage that a λ-dependent boundary condition at a regular endpoint becomes a special case of a λ-dependent boundary condition at a limit-circle endpoint. The simplicity of the spectrum is also built into the formulation given, and the spectral function is shown to have bounded total variation over (−∞, ∞) which is known in terms of the parameters of the λ-dependent boundary condition independently of the limit-circle/limit-point classification at the right endpoint. The theory is applied to the constant coefficient equation in [0, ∞) and the Bessel equation of order zero in (0, ∞), explicit formulae for the spectral function being obtained in each case. Finally, the question is posed as to whether the classical Weyl theory for problems not involving λ in the boundary conditions can also be formulated so as to involve spectral functions having bounded total variation.

We investigate the existence, uniqueness and regularity of solutions to the linear differential equation Lu = f under nonlinear mixed boundary conditions on domains with singular boundary points.

A new method is developed for obtaining the asymptotic form of solutions of the fourth-order differential equation

where m, n are integers and 1 ≦ m, n ≦ 2. The method gives new, shorter proofs of the well-known results of Walker in deficiency index theory and covers the cases not considered by Walker.

The nonlinear operator equation (N), , describes both semilinear elliptic boundary value problems (P) and their natural discretisations (Ph). (Here is a positive compact linear operator and [t]+ ≡ (t + |t|)/2 for all t ∊ ℝ.) It is proved that, for q ≧ 0 (q ≢ 0), in a Banach lattice E the equation (N) has an unbounded continuum ℱ of nontrivial solutions (λ, ψ) ∊ ℝ × E bifurcating from infinity at (λ1, ∞) (here is the first (positive) eigenvalue of ). All nontrivial solutions (λ, ψ) have λ ≧ λ1, and if maps a smaller cone Ks, into itself then there is a ℱs ⊂ℝ×Ks with similar properties to ℱ. The existence theory for (N) is applied to problems (P) and (Ph) which are defined on the simply-connected domain Ω. It is shown that the projection of ℱ on the λ-axis is either unbounded if the continuous function q > 0 except on a set of measure zero in Ω, or is bounded if q ≡ 0 on a subdomain of Ω. If is the second eigenvalue for in (Ph) then there is at most one nontrivial solution for each λ satisfying λ1 < λ < λ2; in the corresponding uniqueness result for (P) q is restricted to being strictly positive somewhere on ∂Ω Additional properties for the solutions of (P) and (Ph) are also proved.

This paper continues the study of the boundary value problem, for (λ, ψ)

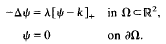
Here δ denotes the Laplacian, k is a given positive constant, and λ1 will denote the first eigenvalue for the Dirichlet problem for −δ on Ω. For λ ≦ λ1, the only solutions are those with ψ = 0. Throughout we will be interested in solutions (λ, ψ) with λ > λ1 and with ψ > 0 in Ω.

In the special case Ω = B(0, R) there is a branch ℱe, of explicit exact solutions which bifurcate from infinity at λ = λ1 and for which the following conclusions are valid, (a) The set Aψ,

is simply-connected, (b) Along ℱe, ψm → k, ‖ψ‖1 → 0 and the diameter of Aψ tends to zero as λ → ∞, where

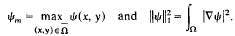
Here it is shown that the above conclusions hold for other choices of Ω, and in particular, for Ω = (−a, a)×(−b, b). (Existence is settled in Part I, and elsewhere.)

The results of numerical and asymptotic calculations when Ω = (−a, a)×(−b, b) are given to illustrate both the above, and some limitations in the conclusions of our analysis.

If ℍ is a rational indefinite quaternion algebra and T is an order of ℍ, let G+(T) denote the subgroup of units u ∊ T with norm n(u) = + 1. For a certain class of orders, Eichler has determined the measure μ(G+(T)) of G+(T), viewed as a Fuchsian group. This is extended to arbitrary orders by methods depending only upon classical number-theory and group theory. As an application, an estimate of the magnitude of a small non-trivial solution of the diophantine Pellian equation

is supplied and the restrictions on the integers D and P associated with previous work on this question are eliminated.

The solutions of stochastic differential equations are used to construct Markov processes on the Banach manifold C(S, M) of continuous maps from a compact metric space S into a smooth complete finite dimensional Riemannian manifold M. In the special case where S is a single point the construction gives a large class of diffusion processes on the manifold M, including (under certain curvature conditions) the Brownian motion process.

It is shown that the elements of the closed operator algebra generated by one-dimensional singular integral operators with piecewise continuous coefficients with a fixed finite set of points of discontinuity can be written as the sum of a singular integral operator, a compact operator, and generalized Mellin convolutions. Their Gohberg-Krupnik symbol is given in terms of the Mellin transform. This gives an explicit construction of an operator with prescribed Gohberg—Krupnik symbol.