Mathematical models of phase transitions in solids lead to the variational problem, minimize ∫Ω W (Du) dx, where W has a multi-well structure, i.e. W = 0 on a multi-well set K and W > 0 otherwise. We study this problem in two dimensions in the case of equal determinant, i.e. for K = SO(2)U1 ∪ … ∪SO(2)Uk or K = O(2)U1 ∪ … ∪ O(2)Uk for U1, … , Uk ∈ M2×2 with det Ui = δ in three dimensions when the matrices Ui are essentially two-dimensional and also for K = SO(3)Û1 ∪ … ∪ SO(3)Ûk for U1, … , Uk ∈ M3×3 with , which arises in the study of thin films. Here, Ûi denotes the (3×2) matrix formed with the first two columns of Ui. We characterize generalized convex hulls, including the quasiconvex hull, of these sets, prove existence of minimizers and identify conditions for the uniqueness of the minimizing Young measure. Finally, we use the characterization of the quasiconvex hull to propose ‘approximate relaxed energies’, quasiconvex functions which vanish on the quasiconvex hull of K and grow quadratically away from it.

We approximate functionals depending on the gradient of u and on the behaviour of u near the discontinuity points by families of non-local functionals where the gradient is replaced by finite differences. We prove pointwise convergence, Γ-convergence and a compactness result, which implies, in particular, the convergence of minima and minimizers.

We study the asymptotic properties of blow-up solutions u = u(x, t) ≥ 0 of the quasilinear heat equation 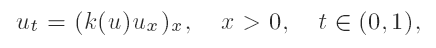, where k(u) is a smooth non-negative function, with a given blowing up regime on the boundary u(0, t) = ψ(t) > 0 for t ∈ (0, 1), where ψ(t) → ∞ as t → 1−, and bounded initial data u(x, 0) ≥ 0. We classify the asymptotic properties of the solutions near the blow-up time, t → 1−, in terms of the heat conductivity coefficient k(u) and of boundary data ψ(t); both are assumed to be monotone. We describe a domain, denoted by , of minimal asymptotics corresponding to the data ψ(t) with a slow growth as t → 1− and a class of nonlinear coefficients k(u).

We prove that for any problem in S11−, such a blow-up singularity is asymptotically structurally equivalent to a singularity of the heat equation ut = uxx described by its self-similar solution of the form u*(x, t) = −ln(1 − t) + g(ξ), ξ = x/(1 − t)1/2, where g solves a linear ordinary differential equation. This particular self-similar solution is structurally stable upon perturbations of the boundary function and also upon nonlinear perturbations of the heat equation with the basin of attraction .

In this paper, we construct three types of symmetric peaked solutions for a Neumann problem involving critical Sobolev exponent: the interior peaked solution, the boundary peaked solution and the interior-boundary peaked solution.

Let f(·, λ) : R→R be given so that f(0, λ) = 0 and f(x, λ) = (1 + λ)x + ax2 + bx3 + o(x3) as x → 0. We characterize those small values of ε > 0 and λ ∈ R for which there are periodic solutions of periods approximately 1/k with k ∈ N of the delay equations When a = 0, these periodic solutions approach square waves if b < 0 or pulses if b > 0 as ε → 0. These results are similar to those obtained by Chow et al. and Hale and Huang, where the case of f(x, λ) = −(1 + λ)x + ax2 + bx3 + o(x3) as x → 0 is considered. However, when a ≠ 0, all these periodic solutions approach pulses as ε → 0; an interesting phenomenon that cannot happen in the case considered by Chow et al. and Hale and Huang.

The creation and propagation of oscillations in a model for the dynamics of fine structure under viscoelastic damping is studied. It is shown that oscillations in the velocity ut are lost immediately as time evolves, while oscillations in the initial strain ux cannot be created, and they persist for all time if initially present. Uniqueness of generalized solutions (Young measures) is obtained, and a characterization of these Young measures is provided in the case of periodic modulated initial data.

We consider a phase-field model for diffusion-induced grain boundary motion. The model couples a parabolic variational inequality to a degenerate diffusion equation. Using a regularization technique, we prove an existence theorem for the resulting system. We also obtain a uniqueness result, provided the solution has some additional regularity.

We develop a spectral theory for the equation (∇ + ieA) × u = ±mu on Minkowski 3-space (one time variable and two space variables); here, A is a real vector potential and the vector product is defined with respect to the Minkowski metric. This equation was formulated by Elton and Vassiliev, who conjectured that it should have properties similar to those of the two-dimensional Dirac equation. Our equation contains a large parameter c (speed of light), and this motivates the study of the asymptotic behaviour of its spectrum as c → +∞. We show that the essential spectrum of our equation is the same as that of Dirac (theorem 3.1), whereas the discrete spectrum agrees with Dirac to a relative accuracy δλ/mc2 ~ O(c−4) (theorem 3.3). In other words, we show that our equation has the same accuracy as the two-dimensional Pauli equation, its advantage over Pauli being relativistic invariance.

This paper contains a rigorous existence theory for three-dimensional steady gravity-capillary finite-depth water waves which are uniformly translating in one horizontal spatial direction x and periodic in the transverse direction z. Physically motivated arguments are used to find a formulation of the problem as an infinite-dimensional Hamiltonian system in which x is the time-like variable, and a centre-manifold reduction technique is applied to demonstrate that the problem is locally equivalent to a finite-dimensional Hamiltonian system. General statements concerning the existence of waves which are periodic or quasiperiodic in x (and periodic in z) are made by applying standard tools in Hamiltonian-systems theory to the reduced equations.

A critical curve in Bond number–Froude number parameter space is identified which is associated with bifurcations of generalized solitary waves. These waves are three dimensional but decay to two-dimensional periodic waves (small-amplitude Stokes waves) far upstream and downstream. Their existence as solutions of the water-wave problem confirms previous predictions made on the basis of model equations.

The functional F(u) = ∫Bf(x, Du) is considered, where B is the unit ball in R2, u varies in the set of the locally Lipschitz functions on R2 and f belongs to a family containing, as model case, the following integrand:

The computation of the relaxed functional F̄ is provided yielding an explicit representation formula.

This formula nevertheless is not integral, because F̄ is not a measure and does not coincide with the obvious extension of F over all W1,p(B).

This phenomenon is essentially due to the non-standard growth behaviour of f(x, z) in the variable z.

We study a predator–prey system with Holling–Tanner interaction terms. We show that if the saturation rate m is large, spatially inhomogeneous steady-state solutions arise, contrasting sharply with the small-m case, where no such solution could exist. Furthermore, for large m, we give sharp estimates on the ranges of other parameters where spatially inhomogeneous solutions can exist. We also determine the asymptotic behaviour of the spatially inhomogeneous solutions as m → ∞, and an interesting relation between this population model and free boundary problems is revealed.

In this paper, we study the asymptotic decay properties in both spatial and temporal variables for a class of weak and strong solutions, by constructing the weak and strong solutions in corresponding weighted spaces. It is shown that, for the strong solution, the rate of temporal decay depends on the rate of spatial decay of the initial data. Such rates of decay are optimal.

We examine the singularly perturbed variational problem in the plane. As ε → 0, this functional favours |∇ψ| = 1 and penalizes singularities where |∇∇ψ| concentrates. Our main result is a compactness theorem: if {Eε(ψε)}ε↓0 is uniformly bounded, then {∇ψε}ε↓0 is compact in L2. Thus, in the limit ε → 0, ψ solves the eikonal equation |∇ψ| = 1 almost everywhere. Our analysis uses ‘entropy relations’ and the ‘div-curl lemma,’ adopting Tartar's approach to the interaction of linear differential equations and nonlinear algebraic relations.

In this paper, we consider non-negative solutions of , We prove that if pq ≤ 1, every solution is global while if pq > 1, all solutions blow up in finite time. We also show that if p, q ≥ 1, then blow-up can occur only on the boundary.

In this paper we consider quasilinear hemivariational inequalities at resonance. We obtain existence theorems using Landesman-Lazer-type conditions and multiplicity theorems for problems with strong resonance at infinity. Our method of proof is based on the non-smooth critical point theory for locally Lipschitz functions and on a generalized version of the Ekeland variational principle.

We prove that, contrary to the L1-Nash inequality, there exists a second best constant for the L2-Nash inequality on any smooth compact Riemannian manif

Keller's phase-interchange relation, which computes the overall conductivity of a two-dimensional checkerboard with alternating conductivity, is revisited in the context of nonlinear incompressible elasticity. A general phase-interchange relation is obtained in a monotone setting through H-convergence and in a convex setting through variational methods. Several Keller-like applications are presented.

Lower semicontinuity and relaxation results in BV are obtained for multiple integrals where the energy density f satisfies lower semicontinuity conditions with respect to (x, u) and is not subjected to coercivity hypotheses. These results call for methods recently developed in the calculus of variations.

We extend and clarify some of observations due to Barron and Jensen concerning the relation between subdifferentials and superdifferentials of a function and extend the comparison principle for semicontinuous solutions of Hamilton–Jacobi equations with convex Hamiltonians to that in infinite-dimensional Hilbert spaces.

Let Ω ⊂ Rn be a bounded domain and let f : Ω × RN × RN×n → R. Consider the functional over the class of Sobolev functions W1,q(Ω;RN) (1 ≤ q ≤ ∞) for which the integral on the right is well defined. In this paper we establish sufficient conditions on a given function u0 and f to ensure that u0 provides an Lr local minimizer for I where 1 ≤ r ≤ ∞. The case r = ∞ is somewhat known and there is a considerable literature on the subject treating the case min(n, N) = 1, mostly based on the field theory of the calculus of variations. The main contribution here is to present a set of sufficient conditions for the case 1 ≤ r < ∞. Our proof is based on an indirect approach and is largely motivated by an argument of Hestenes relying on the concept of ‘directional convergence’.