We review recent theoretical progress in the physical understanding of far-from-equilibrium phenomena seen experimentally in epitaxial growth and erosion on crystal surfaces. The formation and dynamics of various interface structures (pyramids, ripples, etc.), and also kinetic phase transitions observed between these structures, can all be understood within a simple continuum model based on the mass conservation law and respecting the symmetries of the growing crystal surface. In particular, theoretical predictions and experimental results are compared for (001), (110) and (111) crystal surfaces.

The theory of reproducing kernel Hilbert spaces is applied to a minimization problem with prescribed nodes. We re-prove and generalize some results previously obtained by Gunawan et al. [2,3], and also discuss the Hölder continuity of the solution to the problem.

A two-server service network has been studied from the principal-agent perspective. In the model, services are rendered by two independent facilities coordinated by an agency, which seeks to devise a strategy to suitably allocate customers to the facilities and to simultaneously determine compensation levels. Two possible allocation schemes were compared — viz. the common queue and separate queue schemes. The separate queue allocation scheme was shown to give more competition incentives to the independent facilities and to also induce higher service capacity. In this paper, we investigate the general case of a multiple-server queueing model, and again find that the separate queue allocation scheme creates more competition incentives for servers and induces higher service capacities. In particular, if there are no severe diseconomies associated with increasing service capacity, it gives a lower expected sojourn time in equilibrium when the compensation level is sufficiently high.

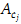The stability of the Nyström method for the Sherman-Lauricella equation on contours with corner points cj, j = 0, 1, …, m relies on the invertibility of certain operators belonging to an algebra of Toeplitz operators. The operators do not depend on the shape of the contour, but on the opening angle θj of the corresponding corner cj and on parameters of the approximation method mentioned. They have a complicated structure and there is no analytic tool to verify their invertibility. To study this problem, the original Nyström method is applied to the Sherman-Lauricella equation on a special model contour that has only one corner point with varying opening angle In the interval (0.1π, 1.9π), it is found that there are 8 values of θj where the invertibility of the operator may fail, so the corresponding original Nyström method on any contour with corner points of such magnitude cannot be stable and requires modification.