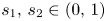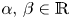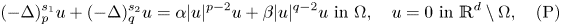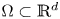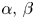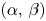1. Introduction and main results
In this paper, we are concerned with the existence and non-existence of positive solutions to the following nonlinear eigenvalue problem involving the fractional $(p,\,q)$![]() -Laplace operator with zero Dirichlet boundary condition:
-Laplace operator with zero Dirichlet boundary condition:
where $0 < s_2 < s_1 < 1 < q < p < \infty$![]() , $\alpha,\, \beta \in \mathbb {R}$
, $\alpha,\, \beta \in \mathbb {R}$![]() are two parameters and $\Omega \subset \mathbb {R}^d$
are two parameters and $\Omega \subset \mathbb {R}^d$![]() is a bounded open set. In general, the fractional $r$
is a bounded open set. In general, the fractional $r$![]() -Laplacian $(-\Delta )^{s}_r$
-Laplacian $(-\Delta )^{s}_r$![]() ($s \in (0,\,1)$
($s \in (0,\,1)$![]() and $r \in (1,\, \infty )$
and $r \in (1,\, \infty )$![]() ) is defined as
) is defined as
where P.V. stands for the principle value.
The local counterpart of (EV; α, β) is the following Dirichlet eigenvalue problem for the $(p,\,q)$![]() -Laplace operator:
-Laplace operator:
The study of $(p,\,q)$![]() -Laplace operators are well known for their applications in physics, chemical reactions, reaction-diffusion equations e.t.c. for details, see [Reference Cherfils and Il'yasov15, Reference Derrick18, Reference Fife20] and the references therein. Some authors considered the eigenvalue problems for the $(p,\,q)$
-Laplace operators are well known for their applications in physics, chemical reactions, reaction-diffusion equations e.t.c. for details, see [Reference Cherfils and Il'yasov15, Reference Derrick18, Reference Fife20] and the references therein. Some authors considered the eigenvalue problems for the $(p,\,q)$![]() -Laplace operator. In this direction, for $\alpha =\beta$
-Laplace operator. In this direction, for $\alpha =\beta$![]() , Motreanu–Tanaka in [Reference Motreanu and Tanaka29] obtained the existence and non-existence of positive solutions of (1.1). For $\alpha \neq \beta$
, Motreanu–Tanaka in [Reference Motreanu and Tanaka29] obtained the existence and non-existence of positive solutions of (1.1). For $\alpha \neq \beta$![]() , in [Reference Bobkov and Tanaka8] Bobkov–Tanaka extended this result by providing a certain region in the $(\alpha,\,\beta )$
, in [Reference Bobkov and Tanaka8] Bobkov–Tanaka extended this result by providing a certain region in the $(\alpha,\,\beta )$![]() -plane that allocates the sets of existence and non-existence of positive solutions of (1.1). Moreover, they constructed a threshold curve in the first quadrant of the $(\alpha,\,\beta )$
-plane that allocates the sets of existence and non-existence of positive solutions of (1.1). Moreover, they constructed a threshold curve in the first quadrant of the $(\alpha,\,\beta )$![]() -plane, which separates these two sets. Later, in [Reference Bobkov and Tanaka9], the same authors plotted a different curve for the existence of ground states and the multiplicity of the positive solutions for (1.1). It is essential that in which region the positive solution of (1.1) exists or does not exist, and the behaviour of the threshold curve depends on whether $\phi _{p},\, \phi _{q}$
-plane, which separates these two sets. Later, in [Reference Bobkov and Tanaka9], the same authors plotted a different curve for the existence of ground states and the multiplicity of the positive solutions for (1.1). It is essential that in which region the positive solution of (1.1) exists or does not exist, and the behaviour of the threshold curve depends on whether $\phi _{p},\, \phi _{q}$![]() are linearly independent, where $\phi _{p} \text { and } \phi _{q}$
are linearly independent, where $\phi _{p} \text { and } \phi _{q}$![]() are the first Dirichlet eigenfunctions of the operators $-\Delta _p$
are the first Dirichlet eigenfunctions of the operators $-\Delta _p$![]() and $-\Delta _q$
and $-\Delta _q$![]() respectively. For other results related to the positive solutions of eigenvalue problems involving $(p,\,q)$
respectively. For other results related to the positive solutions of eigenvalue problems involving $(p,\,q)$![]() -Laplace operator, we refer to [Reference Bai, Papageorgiou and Zeng6, Reference Bobkov and Tanaka10, Reference Tanaka33] and the references therein.
-Laplace operator, we refer to [Reference Bai, Papageorgiou and Zeng6, Reference Bobkov and Tanaka10, Reference Tanaka33] and the references therein.
In the nonlocal case, parallelly, many authors studied the nonlinear equations driven by the sum of fractional $p$![]() -Laplace and fractional $q$
-Laplace and fractional $q$![]() -Laplace operators with the critical exponent. For example, see [Reference Ambrosio2, Reference Ambrosio and Isernia4, Reference Bhakta and Mukherjee7, Reference Giacomoni, Kumar and Sreenadh24, Reference Goel, Kumar and Sreenadh25] where the weak solution's existence, regularity, multiplicity, positivity and other qualitative properties are investigated. The study of (EV; α, β) is motivated by the Dancer–Fučik (DF) spectrum of the fractional $r$
-Laplace operators with the critical exponent. For example, see [Reference Ambrosio2, Reference Ambrosio and Isernia4, Reference Bhakta and Mukherjee7, Reference Giacomoni, Kumar and Sreenadh24, Reference Goel, Kumar and Sreenadh25] where the weak solution's existence, regularity, multiplicity, positivity and other qualitative properties are investigated. The study of (EV; α, β) is motivated by the Dancer–Fučik (DF) spectrum of the fractional $r$![]() -Laplace operator. The DF spectrum of the operator $(-\Delta )^{s}_r$
-Laplace operator. The DF spectrum of the operator $(-\Delta )^{s}_r$![]() is the set of all points $(\alpha,\,\beta )\in \mathbb {R}^2$
is the set of all points $(\alpha,\,\beta )\in \mathbb {R}^2$![]() such that the following problem
such that the following problem
admits a nontrivial weak solution, where $u^{\pm } = \max \{\pm u,\, 0 \}$![]() is the positive and negative part of $u$
is the positive and negative part of $u$![]() . For $r=2$
. For $r=2$![]() , in [Reference Goyal and Sreenadh26], Goyal–Sreenadh considered (1.2) and proved the existence of a first nontrivial curve in the DF spectrum. They also showed that the curve is Lipschitz continuous, strictly decreasing, and studied its asymptotic behaviour. For $r \neq 2$
, in [Reference Goyal and Sreenadh26], Goyal–Sreenadh considered (1.2) and proved the existence of a first nontrivial curve in the DF spectrum. They also showed that the curve is Lipschitz continuous, strictly decreasing, and studied its asymptotic behaviour. For $r \neq 2$![]() , in [Reference Perera, Squassina and Yang31], the authors constructed an unbounded sequence of decreasing curves in the DF spectrum. Nevertheless, the study of the spectrum for the fractional $(p,\,q)$
, in [Reference Perera, Squassina and Yang31], the authors constructed an unbounded sequence of decreasing curves in the DF spectrum. Nevertheless, the study of the spectrum for the fractional $(p,\,q)$![]() -Laplace operator is not well explored. In [Reference Nguyen and Vo30], for $\alpha =\beta$
-Laplace operator is not well explored. In [Reference Nguyen and Vo30], for $\alpha =\beta$![]() , Nguyen-Vo studied the following weighted eigenvalue problem with zero Dirichlet boundary condition:
, Nguyen-Vo studied the following weighted eigenvalue problem with zero Dirichlet boundary condition:
where $0< s_2< s_1< 1< q \le p< \infty$![]() , the weights $m_p,\, m_q$
, the weights $m_p,\, m_q$![]() are bounded in $\Omega$
are bounded in $\Omega$![]() and satisfy $m_p^+,\, m_q^+ \not \equiv 0$
and satisfy $m_p^+,\, m_q^+ \not \equiv 0$![]() . Depending on the values of $\alpha$
. Depending on the values of $\alpha$![]() , the authors obtained the existence and non-existence of positive solutions of (1.3).
, the authors obtained the existence and non-existence of positive solutions of (1.3).
The primary aim of this paper can be summarized into the following two aspects:
(a) We provide a comprehensive analysis of the sets in the $(\alpha,\, \beta )$
 -plane that determine the existence and non-existence of positive solutions for the equation (EV; α, β). Following the local case approach, we construct a continuous threshold curve denoted as $\mathcal {C}$
-plane that determine the existence and non-existence of positive solutions for the equation (EV; α, β). Following the local case approach, we construct a continuous threshold curve denoted as $\mathcal {C}$ that effectively separates the regions where positive solutions exist from those where they do not. In some specific regions of the $(\alpha,\, \beta )$
that effectively separates the regions where positive solutions exist from those where they do not. In some specific regions of the $(\alpha,\, \beta )$ -plane, we employ the sub-super solutions technique to establish the existence of positive solutions. To apply this technique, we utilize the crucial result stated in theorem 4.1, which proves that every nonnegative solution of (EV; α, β) is globally bounded.
-plane, we employ the sub-super solutions technique to establish the existence of positive solutions. To apply this technique, we utilize the crucial result stated in theorem 4.1, which proves that every nonnegative solution of (EV; α, β) is globally bounded.(b) The existence and non-existence of positive solutions to (EV; α, β) depend on the following statement:
(LI)\begin{equation} \phi_{s_1,p} \neq c \phi_{s_2,q} \text{ for any } c \in {\mathbb{R}}, \end{equation}where $\phi _{s_1,p} \text { and } \phi _{s_2,q}$
 are the first eigenfunctions of the operators $(-\Delta )_p^{s_1}$
are the first eigenfunctions of the operators $(-\Delta )_p^{s_1}$ and $(-\Delta )_q^{s_2}$
and $(-\Delta )_q^{s_2}$ corresponding to the first eigenvalues $\lambda _{s_1,p}^1$
corresponding to the first eigenvalues $\lambda _{s_1,p}^1$ and $\lambda _{s_2,q}^1$
and $\lambda _{s_2,q}^1$ respectively in $\Omega$
respectively in $\Omega$ under zero Dirichlet boundary condition. While this linear independence condition for the operators $-\Delta _p$
under zero Dirichlet boundary condition. While this linear independence condition for the operators $-\Delta _p$ and $-\Delta _q$
and $-\Delta _q$ was conjectured in [Reference Bobkov and Tanaka8] and later proved in [Reference Bobkov and Tanaka9], its validity remains unknown for any $s_1,\, s_2 \in (0,\,1)$
was conjectured in [Reference Bobkov and Tanaka8] and later proved in [Reference Bobkov and Tanaka9], its validity remains unknown for any $s_1,\, s_2 \in (0,\,1)$ . Nevertheless, several authors have assumed the condition (LI) in various contexts (e.g., [Reference Giacomoni, Gouasmia and Mokrane23, Reference Nguyen and Vo30]). We establish the validity of (LI) under certain assumptions on $s_1$
. Nevertheless, several authors have assumed the condition (LI) in various contexts (e.g., [Reference Giacomoni, Gouasmia and Mokrane23, Reference Nguyen and Vo30]). We establish the validity of (LI) under certain assumptions on $s_1$ and $s_2$
and $s_2$ , as demonstrated in theorem 1.9.
, as demonstrated in theorem 1.9.
Recall that, for $0< s<1\leq r<\infty$![]() , the fractional Sobolev space is defined as
, the fractional Sobolev space is defined as
with the so-called fractional Sobolev norm ${\lVert }{u}{\rVert }_{s,r,\Omega } :=(\|u\|_{L^r(\Omega )}^r + [u]_{s,r,\Omega }^r)^\frac {1}{r},\,$![]() where
where

is called the Gagliardo seminorm. For $r \in (1,\,\infty )$![]() , $W^{s,r}(\Omega )$
, $W^{s,r}(\Omega )$![]() is a reflexive Banach space with respect to the fractional Sobolev norm ${\lVert }{\cdot }{\rVert }_{s,r,\Omega }$
is a reflexive Banach space with respect to the fractional Sobolev norm ${\lVert }{\cdot }{\rVert }_{s,r,\Omega }$![]() . Now we consider the following closed subspace of $W^{s,r}(\mathbb {R}^d)$
. Now we consider the following closed subspace of $W^{s,r}(\mathbb {R}^d)$![]() :
:
endowed with the seminorm $[\cdot ]_{s,r,\mathbb {R}^d}$![]() , which is an equivalent norm in $W_0^{s,r}(\Omega )$
, which is an equivalent norm in $W_0^{s,r}(\Omega )$![]() ([Reference Brasco, Lindgren and Parini12, Lemma 2.4]). For details of the fractional Sobolev spaces and their related embedding results, we refer to [Reference Brasco, Lindgren and Parini12, Reference Brasco and Parini14, Reference Di Nezza, Palatucci and Valdinoci19] and the references therein. For $s_1 > s_2$
([Reference Brasco, Lindgren and Parini12, Lemma 2.4]). For details of the fractional Sobolev spaces and their related embedding results, we refer to [Reference Brasco, Lindgren and Parini12, Reference Brasco and Parini14, Reference Di Nezza, Palatucci and Valdinoci19] and the references therein. For $s_1 > s_2$![]() and $p > q \geq 1$
and $p > q \geq 1$![]() , the continuous embedding ${W_0^{s_1,p}(\Omega )} \hookrightarrow {W_0^{s_2,q}(\Omega )}$
, the continuous embedding ${W_0^{s_1,p}(\Omega )} \hookrightarrow {W_0^{s_2,q}(\Omega )}$![]() (see [Reference Antil and Warma5, Proposition 2.2]) allows us to introduce the notion of weak solution for (EV; α, β) in the following sense:
(see [Reference Antil and Warma5, Proposition 2.2]) allows us to introduce the notion of weak solution for (EV; α, β) in the following sense:
Definition 1.1 A function $u\in {W_0^{s_1,p}(\Omega )}$![]() is called a weak solution of (EV; α, β) if the following identity holds for all $\phi \in {W_0^{s_1,p}(\Omega )}$
is called a weak solution of (EV; α, β) if the following identity holds for all $\phi \in {W_0^{s_1,p}(\Omega )}$![]() :
:

In our first theorem, we prove the existence of a positive solution for (EV; α, β) if any of $\alpha$![]() and $\beta$
and $\beta$![]() is larger than the first Dirichlet eigenvalue of the fractional $p$
is larger than the first Dirichlet eigenvalue of the fractional $p$![]() -Laplacian and fractional $q$
-Laplacian and fractional $q$![]() -Laplacian respectively. We also show that this range of $\alpha,\, \beta$
-Laplacian respectively. We also show that this range of $\alpha,\, \beta$![]() is necessary for the existence of a positive solution when (LI) does not hold.
is necessary for the existence of a positive solution when (LI) does not hold.
Theorem 1.2 Let $0 < s_2 < s_1 < 1 < q < p < \infty$![]() . Assume that
. Assume that

The following hold (see Fig. 1):
(i) (Sufficient condition): Let $\alpha,\, \beta$
 satisfy (1.4). In the case, when $\alpha = \lambda _{s_1,p}^1$
satisfy (1.4). In the case, when $\alpha = \lambda _{s_1,p}^1$ and $\beta = \lambda _{s_2,q}^1$
and $\beta = \lambda _{s_2,q}^1$ , we assume that (LI) violates. Then (EV; α, β) admits a positive solution.
, we assume that (LI) violates. Then (EV; α, β) admits a positive solution.(ii) (Necessary condition): Let (LI) violates and (EV; α, β) admits a positive solution. Then $\alpha,\, \beta$
 satisfy (1.4).
satisfy (1.4).

Figure 1. Shaded region denotes existence, and unshaded region denotes non-existence of positive solutions. (a) The case (LI) holds (with $\alpha ^*_{s_1,p} < \infty$![]() ), (b) The case (LI) does not hold.
), (b) The case (LI) does not hold.
Remark 1.3
(i) The above theorem asserts that (EV; $\lambda _{s_1,p}^1,\,\lambda _{s_2,q}^1$
 ) admits a positive solution if and only if (LI) violates. Indeed, (EV; $\lambda _{s_1,p}^1,\,\lambda _{s_2,q}^1$
) admits a positive solution if and only if (LI) violates. Indeed, (EV; $\lambda _{s_1,p}^1,\,\lambda _{s_2,q}^1$ ) admits a non-trivial solution only when (LI) violates (see proposition 6.1).
) admits a non-trivial solution only when (LI) violates (see proposition 6.1).(ii) If (LI) violates, then theorem 1.2 gives a complete description of the set of existence and non-existence of positive solutions of (EV; α, β). In particular, theorem 1.2 generalizes the result of [Reference Nguyen and Vo30, Theorem 1.1] for $\alpha \neq \beta$
 .
.
It is observed that for $\alpha,\,\beta \in \mathbb {R}$![]() , the problem (EV; α, β) is equivalent to the problem (EV; $\beta + \theta,\, \beta$
, the problem (EV; α, β) is equivalent to the problem (EV; $\beta + \theta,\, \beta$![]() ), where $\theta = \alpha -\beta.$
), where $\theta = \alpha -\beta.$![]() Using this terminology we define the following curve:
Using this terminology we define the following curve:
Definition 1.4 Threshold curve
For brevity, denote $\beta = \lambda$![]() . For each $\theta \in \mathbb {R}$
. For each $\theta \in \mathbb {R}$![]() consider the following quantity:
consider the following quantity:
If such $\lambda$![]() does not exist, we then set $\lambda ^*(\theta ) = -\infty.$
does not exist, we then set $\lambda ^*(\theta ) = -\infty.$![]() The threshold curve corresponding to (EV; α, β) is defined as $\mathcal {C} := \{(\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )): \theta \in {\mathbb {R}}\}$
The threshold curve corresponding to (EV; α, β) is defined as $\mathcal {C} := \{(\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )): \theta \in {\mathbb {R}}\}$![]() . Also, we define the following quantities:
. Also, we define the following quantities:

Clearly, $\theta ^* \leq \theta ^*_+$![]() and $\theta ^* = \theta ^*_+$
and $\theta ^* = \theta ^*_+$![]() if and only if (LI) violates (from (iv) of proposition 2.1).
if and only if (LI) violates (from (iv) of proposition 2.1).
In the following proposition, we discuss some qualitative properties of $\mathcal {C}$![]() and see that $\mathcal {C}$
and see that $\mathcal {C}$![]() carries similar behaviours as in the local case [Reference Bobkov and Tanaka8, Proposition 3 and Figure 2].
carries similar behaviours as in the local case [Reference Bobkov and Tanaka8, Proposition 3 and Figure 2].
Proposition 1.5 Let $0 < s_2 < s_1 < 1 < q < p < \infty$![]() . Then the following hold:
. Then the following hold:
(i) $\lambda ^*(\theta ) < \infty$
 for all $\theta \in \mathbb {R}$
for all $\theta \in \mathbb {R}$ .
.(ii) $\lambda ^*(\theta ^*) + \theta ^* > \lambda ^1_{s_1,p}$
 and $\lambda ^*(\theta ^*) > \lambda ^1_{s_2,q}$
and $\lambda ^*(\theta ^*) > \lambda ^1_{s_2,q}$ if and only if (LI) holds.
if and only if (LI) holds.(iii) $\lambda ^*(\theta ) + \theta \geq \lambda ^1_{s_1,p}$
 and $\lambda ^*(\theta ) \geq \lambda ^1_{s_2,q}$
and $\lambda ^*(\theta ) \geq \lambda ^1_{s_2,q}$ for all $\theta \in \mathbb {R}.$
for all $\theta \in \mathbb {R}.$
(iv) $\lambda ^*(\theta )$
 is decreasing and $\lambda ^*(\theta ) + \theta$
is decreasing and $\lambda ^*(\theta ) + \theta$ is increasing on $\mathbb {R}.$
is increasing on $\mathbb {R}.$
(v) If $\alpha ^*_{s_1,p}$
 is finite, then $\lambda ^*(\theta ) = \lambda ^1_{s_2,q}$
is finite, then $\lambda ^*(\theta ) = \lambda ^1_{s_2,q}$ for all $\theta \geq \theta ^*_+.$
for all $\theta \geq \theta ^*_+.$
(vi) $\lambda ^*$
 is continuous on $\mathbb {R}.$
is continuous on $\mathbb {R}.$
According to (iii) of the above proposition, $\mathcal {C} \subset ([\lambda _{s_1,p}^1,\, \infty ) \times [\lambda _{s_2,q}^1,\, \infty ))$![]() . Further, if $\alpha ^*_{s_1,p} = \infty$
. Further, if $\alpha ^*_{s_1,p} = \infty$![]() , from the property (iii), we observe that $\mathcal {C}$
, from the property (iii), we observe that $\mathcal {C}$![]() always lies above the line $\beta = \lambda _{s_2,q}^1$
always lies above the line $\beta = \lambda _{s_2,q}^1$![]() . From now onwards, we assume that $\alpha ^*_{s_1, p} < \infty$
. From now onwards, we assume that $\alpha ^*_{s_1, p} < \infty$![]() . In the following theorem, we demonstrate that $\mathcal {C}$
. In the following theorem, we demonstrate that $\mathcal {C}$![]() separates the sets of existence and non-existence of positive solutions in the region $([\lambda _{s_1,p}^1,\, \infty ) \times [\lambda _{s_2,q}^1,\, \infty ))$
separates the sets of existence and non-existence of positive solutions in the region $([\lambda _{s_1,p}^1,\, \infty ) \times [\lambda _{s_2,q}^1,\, \infty ))$![]() (see Fig. 1).
(see Fig. 1).
Theorem 1.6 Let $0 < s_2 < s_1 < 1 < q < p < \infty$![]() . Let $\alpha \ge \lambda _{s_1,p}^1$
. Let $\alpha \ge \lambda _{s_1,p}^1$![]() and $\beta \ge \lambda _{s_2,q}^1$
and $\beta \ge \lambda _{s_2,q}^1$![]() . Assume that (LI) holds.
. Assume that (LI) holds.
(i) If $\beta \in (\lambda _{s_2,q}^1,\, \lambda ^*(\theta ))$
 , then (EV; α, β) admits a positive solution.
, then (EV; α, β) admits a positive solution.(ii) If $\alpha > \lambda _{s_1,p}^1$
 and $\beta < \lambda ^*(\theta )$
and $\beta < \lambda ^*(\theta )$ , then (EV; α, β) admits a positive solution.
, then (EV; α, β) admits a positive solution.(iii) If $\beta > \lambda ^*(\theta )$
 , then there does not exist any positive solution for (EV; α, β).
, then there does not exist any positive solution for (EV; α, β).
Now we state the existence and non-existence of positive solutions on the curve $\mathcal {C}$![]() (see Fig. 1).
(see Fig. 1).
Theorem 1.7 Let $0 < s_2 < s_1 < 1 < q < p < \infty$![]() .
.
(i) If $\theta < \theta ^*_+$
 , then (EV; $\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )$
, then (EV; $\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )$ ) admits a positive solution.
) admits a positive solution.(ii) If $\theta > \theta ^*_+$
 , then there does not exist any positive solution for (EV; $\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )$
, then there does not exist any positive solution for (EV; $\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )$ ).
).
The above theorem does not consider the borderline case $\theta = \theta _+^*$![]() . In this case, we have a partial result in remark 6.9, which says that (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$
. In this case, we have a partial result in remark 6.9, which says that (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$![]() ) does not admit any ground state solution.
) does not admit any ground state solution.
Remark 1.8 The relations among $s_1,\, s_2,\, p,\, q$![]() are taken without loss of any generality. All the preceding results in this paper hold for the remaining cases by choosing the appropriate solution space as given below:
are taken without loss of any generality. All the preceding results in this paper hold for the remaining cases by choosing the appropriate solution space as given below:
(i) For $s_1 < s_2$
 and $p < q$
and $p < q$ (symmetric), we choose the solution space as ${W_0^{s_2,q}(\Omega )}$
(symmetric), we choose the solution space as ${W_0^{s_2,q}(\Omega )}$ .
.(ii) For $s_2 < s_1$
 and $p< q$
and $p< q$ (cross), we choose the solution space as ${W_0^{s_1,p}(\Omega )} \cap {W_0^{s_2,q}(\Omega )}$
(cross), we choose the solution space as ${W_0^{s_1,p}(\Omega )} \cap {W_0^{s_2,q}(\Omega )}$ endowed with the norm $[\cdot ]_{s_1,p,\mathbb {R}^d}+[\cdot ]_{s_2,q,\mathbb {R}^d}$
endowed with the norm $[\cdot ]_{s_1,p,\mathbb {R}^d}+[\cdot ]_{s_2,q,\mathbb {R}^d}$ .
.(iii) For $s_1 = s_2=s$
 and $p \neq q$
and $p \neq q$ , we choose the solution space as $W^{s,p}_0(\Omega ) \cap W^{s,q}_0(\Omega )$
, we choose the solution space as $W^{s,p}_0(\Omega ) \cap W^{s,q}_0(\Omega )$ endowed with the norm $[\cdot ]_{s,p,\mathbb {R}^d}+[\cdot ]_{s,q,\mathbb {R}^d}$
endowed with the norm $[\cdot ]_{s,p,\mathbb {R}^d}+[\cdot ]_{s,q,\mathbb {R}^d}$ .
.
The next theorem verifies the linear independency of the first Dirichlet eigenfunctions of the fractional $p$![]() -Laplacian and the fractional $q$
-Laplacian and the fractional $q$![]() -Laplacian.
-Laplacian.
Theorem 1.9 Let $1< q< p<\infty$![]() and $s_1,\, s_2 \in (0,\,1)$
and $s_1,\, s_2 \in (0,\,1)$![]() satisfy the following condition:
satisfy the following condition:
Then the set $\{\phi _{s_1, p} ,\, \phi _{s_2, q}\}$![]() is linearly independent.
is linearly independent.
Remark 1.10 Theorem 1.9 holds if we take the other relations among $s_1,\, s_2,\, p,\, q$![]() listed below:
listed below:
(i) For $1< p< q<\infty$
 and $\frac {s_2 {q^{\prime }}}{{p^{\prime }}} < s_1 < s_2$
and $\frac {s_2 {q^{\prime }}}{{p^{\prime }}} < s_1 < s_2$ (interchanging the roles of $s_1,\, s_2,\, p,\, q$
(interchanging the roles of $s_1,\, s_2,\, p,\, q$ ).
).(ii) For $1 < q< p<\infty$
 and $s_1=s_2$
and $s_1=s_2$ .
.
The rest of the paper is organized as follows. Section 2 briefly discusses the first Dirichlet eigenpair of fractional $r$![]() -Laplace operator, recalls the discrete Picone's inequalities, and proves some technical results. In § 3, we prove the validity of (LI). This section contains the proof of theorem 1.9. In § 4, we establish the regularity of the solution for (EV; α, β) and state a version of the strong maximum principle related to (EV; α, β). Section 5 studies various frameworks of energy functionals associated with (EV; α, β). Finally, § 6 studies the existence and non-existence of positive solutions for (EV; α, β). In this section, we prove theorem 1.2–1.7 and proposition 1.5.
-Laplace operator, recalls the discrete Picone's inequalities, and proves some technical results. In § 3, we prove the validity of (LI). This section contains the proof of theorem 1.9. In § 4, we establish the regularity of the solution for (EV; α, β) and state a version of the strong maximum principle related to (EV; α, β). Section 5 studies various frameworks of energy functionals associated with (EV; α, β). Finally, § 6 studies the existence and non-existence of positive solutions for (EV; α, β). In this section, we prove theorem 1.2–1.7 and proposition 1.5.
2. Preliminaries
In this section, we recall some qualitative properties of the first nonlocal eigenvalue and its corresponding eigenfunction. Afterwards, we recall the discrete Picone's identities. We list the following notations to be used in this paper:
Notation:
• $B_R(x)\subset \mathbb {R}^d$
 denotes an open ball of radius $R>0$
denotes an open ball of radius $R>0$ centred at $x.$
centred at $x.$
• For a set $E\subset \mathbb {R}^d$
 , $|E|$
, $|E|$ denotes the Lebesgue measure of $E$
denotes the Lebesgue measure of $E$ .
.• We denote ${\rm d}\mu _1:= {\mid }{x-y}{\mid }^{-(d+s_1p)} {\rm d}x {\rm d}y$
 and ${\rm d}\mu _2:= {\mid }{x-y}{\mid }^{-(d+s_2q)} {\rm d}x {\rm d}y$
and ${\rm d}\mu _2:= {\mid }{x-y}{\mid }^{-(d+s_2q)} {\rm d}x {\rm d}y$ .
.• For $r \in (1,\, \infty )$
 , the conjugate of $r$
, the conjugate of $r$ is denoted as $r^{\prime }:=\frac {r}{r-1}$
is denoted as $r^{\prime }:=\frac {r}{r-1}$ .
.• For $0 < s < 1 < r < \infty$
 , we denote $[\cdot ]_{s,r,\mathbb {R}^d}$
, we denote $[\cdot ]_{s,r,\mathbb {R}^d}$ as $[\cdot ]_{s,r}$
as $[\cdot ]_{s,r}$ , and ${\lVert }{\cdot }{\rVert }_{L^r(\Omega )}$
, and ${\lVert }{\cdot }{\rVert }_{L^r(\Omega )}$ as ${\lVert }{\cdot }{\rVert }_r$
as ${\lVert }{\cdot }{\rVert }_r$ .
.• For $k \in \mathbb {N}$
 , we denote $u_k(x) := u(x) + \frac {1}{k}$
, we denote $u_k(x) := u(x) + \frac {1}{k}$ where $x \in \mathbb {R}^d$
where $x \in \mathbb {R}^d$ .
.• For $\gamma \in (0,\,1)$
 , the Hölder seminorm $[f]_{C^{0, \gamma }(\Omega )} := \underset {x,\,y \in \Omega,\, x \neq y}{\sup } \displaystyle \frac {{\mid }{f(x)- f(y)}{\mid }}{{\mid }{x-y}{\mid }^{\gamma }}$
, the Hölder seminorm $[f]_{C^{0, \gamma }(\Omega )} := \underset {x,\,y \in \Omega,\, x \neq y}{\sup } \displaystyle \frac {{\mid }{f(x)- f(y)}{\mid }}{{\mid }{x-y}{\mid }^{\gamma }}$ .
.• For $sr < d$
 (where $0 < s < 1 < r < \infty$
(where $0 < s < 1 < r < \infty$ ), the fractional critical exponent $\displaystyle r^*_s := \frac {rd}{d-sr}$
), the fractional critical exponent $\displaystyle r^*_s := \frac {rd}{d-sr}$ .
.• For each $n \in \mathbb {N}$
 , we denote the positive and negative parts $(f_n)^{\pm }$
, we denote the positive and negative parts $(f_n)^{\pm }$ by $f_n^{\pm } := \max \{\pm f_n,\, 0\}$
by $f_n^{\pm } := \max \{\pm f_n,\, 0\}$ .
.• Eigenvalue of (2.1), $\lambda _{s,r}(\Omega )$
 is denoted as $\lambda _{s,r}$
is denoted as $\lambda _{s,r}$ .
.• We denote the eigenfunction of (2.1) corresponding to the first eigenvalue $\lambda ^1_{s, r}$
 as $\phi _{s,r}$
as $\phi _{s,r}$ .
.• For $r \in (1,\, \infty )$
 , $x_0 \in \Omega$
, $x_0 \in \Omega$ and $R>0$
and $R>0$ , the nonlocal tail of $f \in W^{s,r}_0(\Omega )$
, the nonlocal tail of $f \in W^{s,r}_0(\Omega )$ is defined as
\begin{align*} \mathrm{Tail}_r(f;x_0,R) := \left(R^{sr}\int_{\mathbb{R}^d\setminus B_R(x_0)}\frac{|f(x)|^{r-1}}{|x-x_0|^{d+sr}}\,{\rm d}x\right)^{\frac{1}{r-1}}. \end{align*}
is defined as
\begin{align*} \mathrm{Tail}_r(f;x_0,R) := \left(R^{sr}\int_{\mathbb{R}^d\setminus B_R(x_0)}\frac{|f(x)|^{r-1}}{|x-x_0|^{d+sr}}\,{\rm d}x\right)^{\frac{1}{r-1}}. \end{align*}
• $C$
 is denoted as a generic positive constant.
is denoted as a generic positive constant.
2.1 First eigenvalue of fractional $r$ -Laplacian
-Laplacian
For a bounded open set $\Omega \subset \mathbb {R}^d$![]() and $0 < s < 1 < r < \infty$
and $0 < s < 1 < r < \infty$![]() , we consider the following nonlinear eigenvalue problem:
, we consider the following nonlinear eigenvalue problem:
We say $\lambda _{s,r}$![]() is an eigenvalue of (2.1), if there exists non-zero $u \in {W_0^{s,r}(\Omega )}$
is an eigenvalue of (2.1), if there exists non-zero $u \in {W_0^{s,r}(\Omega )}$![]() satisfying the following identity for all $\phi \in {W_0^{s,r}(\Omega )}$
satisfying the following identity for all $\phi \in {W_0^{s,r}(\Omega )}$![]() :
:

In this case, $u$![]() is called an eigenfunction corresponding to $\lambda _{s,r}$
is called an eigenfunction corresponding to $\lambda _{s,r}$![]() , and we denote $( \lambda _{s,r},\, u )$
, and we denote $( \lambda _{s,r},\, u )$![]() as an eigenpair. In the following proposition, we collect some qualitative properties of the first eigenpair of (2.1).
as an eigenpair. In the following proposition, we collect some qualitative properties of the first eigenpair of (2.1).
Proposition 2.1 For $r \in (1,\, \infty )$![]() and $s \in (0,\,1)$
and $s \in (0,\,1)$![]() , consider the following quantity:
, consider the following quantity:
Then the following hold:
(i) $\lambda ^1_{s,r}$
 is the first positive eigenvalue of (2.1).
is the first positive eigenvalue of (2.1).(ii) Every eigenfunction corresponding to $\lambda ^1_{s,r}$
 has a constant sign in $\Omega$
has a constant sign in $\Omega$ .
.(iii) If $v$
 is an eigenfunction of (2.1) corresponding to an eigenvalue $\lambda _{s,r}>0$
is an eigenfunction of (2.1) corresponding to an eigenvalue $\lambda _{s,r}>0$ such that $v>0$
such that $v>0$ a.e. in $\Omega$
a.e. in $\Omega$ , then $\lambda _{s,r}=\lambda ^1_{s,r}$
, then $\lambda _{s,r}=\lambda ^1_{s,r}$ .
.(iv) Any two eigenfunctions corresponding to $\lambda ^1_{s,r}$
 are constant multiple of each other.
are constant multiple of each other.(v) Any eigenfunction of (2.1) corresponding to an eigenvalue $\lambda _{s,r}$
 is in $L^{\sigma }(\mathbb {R}^d)$
is in $L^{\sigma }(\mathbb {R}^d)$ for every $\sigma \in [1,\, \infty ]$
for every $\sigma \in [1,\, \infty ]$ . Moreover, if $\Omega$
. Moreover, if $\Omega$ is of class $C^{1,1}$
is of class $C^{1,1}$ , then the eigenfunction lies in $C^{0, \gamma }(\overline {\Omega })$
, then the eigenfunction lies in $C^{0, \gamma }(\overline {\Omega })$ for some $\gamma \in (0,\,s]$
for some $\gamma \in (0,\,s]$ .
.
Proof. For proof of (i) and (iii), we refer to [Reference Franzina and Palatucci21, Lemma 2.1 and Theorem 4.1]. For (ii), see [Reference Brasco and Parini14, Proposition 2.6]. Then the proof of (iv) follows using [Reference Franzina and Palatucci21, Theorem 4.2].
(v) Let $u$![]() be an eigenfunction of (2.1) corresponding to $\lambda _{s,r}$
be an eigenfunction of (2.1) corresponding to $\lambda _{s,r}$![]() . By [Reference Brasco, Lindgren and Parini12, Theorem 3.3], $u \in L^{\infty }( \Omega )$
. By [Reference Brasco, Lindgren and Parini12, Theorem 3.3], $u \in L^{\infty }( \Omega )$![]() and hence $u \in L^{\infty }( \mathbb {R}^d )$
and hence $u \in L^{\infty }( \mathbb {R}^d )$![]() . Further, since $u\in W^{s,r}(\mathbb {R}^d) \cap L^\infty (\mathbb {R}^d)$
. Further, since $u\in W^{s,r}(\mathbb {R}^d) \cap L^\infty (\mathbb {R}^d)$![]() , the interpolation argument yields $u \in L^{\sigma }(\mathbb {R}^d)$
, the interpolation argument yields $u \in L^{\sigma }(\mathbb {R}^d)$![]() for every $\sigma \geq r$
for every $\sigma \geq r$![]() . Also for $\sigma \in [1,\, r)$
. Also for $\sigma \in [1,\, r)$![]() , applying Hölder's inequality with the conjugate pair $(\frac {r}{\sigma },\, \frac {r - \sigma }{\sigma })$
, applying Hölder's inequality with the conjugate pair $(\frac {r}{\sigma },\, \frac {r - \sigma }{\sigma })$![]() ,
,
Thus, $u \in L^{\sigma }(\mathbb {R}^d)$![]() for every $\sigma \in [1,\, \infty ]$
for every $\sigma \in [1,\, \infty ]$![]() . Furthermore, since $u \in L^{\infty }(\mathbb {R}^d)$
. Furthermore, since $u \in L^{\infty }(\mathbb {R}^d)$![]() we apply [Reference Iannizzotto, Mosconi and Squassina27, Theorem 1.1] to get $u \in C^{0, \gamma }(\overline {\Omega })$
we apply [Reference Iannizzotto, Mosconi and Squassina27, Theorem 1.1] to get $u \in C^{0, \gamma }(\overline {\Omega })$![]() for some $\gamma \in (0,\,s]$
for some $\gamma \in (0,\,s]$![]() .
.
2.2 Some important results
In this subsection, we state some elementary inequalities, recall Picone's inequalities for nonlocal operators and collect some test functions in $W^{s,r}_{0}(\Omega )$![]() .
.
Lemma 2.2 Let $a,\, b \in {\mathbb {R}}$![]() , and $\gamma \in {\mathbb {R}}^+$
, and $\gamma \in {\mathbb {R}}^+$![]() . The following hold:
. The following hold:
(i) If $\gamma >1$
 , then
\begin{align*} & {\mid}{a-b}{\mid}^{\gamma-2}(a-b)(a^+{-} b^+) \ge {\mid}{a^+{-} b^+}{\mid}^{\gamma}; \\ & {\mid}{a - b}{\mid}^{\gamma-2}(a-b)(b^{-} - a^{-}) \ge {\mid}{a^{-} - b^{-}}{\mid}^{\gamma}, \end{align*}where $a^{\pm } = \max \{\pm a,\,0\}$
, then
\begin{align*} & {\mid}{a-b}{\mid}^{\gamma-2}(a-b)(a^+{-} b^+) \ge {\mid}{a^+{-} b^+}{\mid}^{\gamma}; \\ & {\mid}{a - b}{\mid}^{\gamma-2}(a-b)(b^{-} - a^{-}) \ge {\mid}{a^{-} - b^{-}}{\mid}^{\gamma}, \end{align*}where $a^{\pm } = \max \{\pm a,\,0\}$
 .
.(ii) If $\gamma \ge 2$
 , then ${\mid }{a-b}{\mid }^{\gamma -2}(a-b) \le C ( {\mid }{a}{\mid }^{\gamma -2}a - {\mid }{b}{\mid }^{\gamma -2}b )$
, then ${\mid }{a-b}{\mid }^{\gamma -2}(a-b) \le C ( {\mid }{a}{\mid }^{\gamma -2}a - {\mid }{b}{\mid }^{\gamma -2}b )$ for some $C = C(\gamma )>0$
for some $C = C(\gamma )>0$ .
.(iii) ${\mid }{{\mid }{a}{\mid }^{\gamma } - {\mid }{b}{\mid }^{\gamma }}{\mid } \le \gamma ( {\mid }{a}{\mid }^{\gamma -1} + {\mid }{b}{\mid }^{\gamma -1} ) {\mid }{a-b}{\mid }$
 .
.
Proof. Proof of (i) follows from [Reference Brasco and Parini14, Lemma A.2]. Proof of (ii) follows from [Reference Iannizzotto, Mosconi and Squassina28, (2.2) of Page 5]. Proof of (iii) follows using the fundamental theorem of calculus.
We recall several versions of the discrete Picone's inequality that are useful in proving our results.
Lemma 2.3 Discrete Picone's inequality
Let $r_1 ,\, r_2 \in (1 ,\, \infty )$![]() with $r_2 \leq r_1$
with $r_2 \leq r_1$![]() and let $f,\, g: \mathbb {R}^d \to \mathbb {R}$
and let $f,\, g: \mathbb {R}^d \to \mathbb {R}$![]() be two measurable functions with $f > 0,\, \; g \ge 0$
be two measurable functions with $f > 0,\, \; g \ge 0$![]() . Then the following hold:
. Then the following hold:
(i) For $x,\, y \in \mathbb {R}^d$
 ,
\begin{align*} & |f(x)-f(y)|^{r_1-2}(f(x)-f(y)) \left(\displaystyle\frac{g(x)^{r_2}}{f(x)^{r_2-1}} - \frac{g(y)^{r_2}}{f(y)^{r_2-1}} \right)\\ & \quad \le {\mid}{g(x)-g(y)}{\mid}^{r_2} {\mid}{f(x)-f(y)}{\mid}^{r_1-r_2}. \end{align*}
,
\begin{align*} & |f(x)-f(y)|^{r_1-2}(f(x)-f(y)) \left(\displaystyle\frac{g(x)^{r_2}}{f(x)^{r_2-1}} - \frac{g(y)^{r_2}}{f(y)^{r_2-1}} \right)\\ & \quad \le {\mid}{g(x)-g(y)}{\mid}^{r_2} {\mid}{f(x)-f(y)}{\mid}^{r_1-r_2}. \end{align*}
(ii) For $x,\,y \in \mathbb {R}^d$
 ,
\begin{align*} & |f(x)-f(y)|^{r_2-2}(f(x)-f(y)) \left(\frac{ g(x)^{r_1}}{f(x)^{r_1-1}}-\frac{ g(y)^{r_1}}{f(y)^{r_1-1}} \right) \\ & \quad \le |g(x)-g(y)|^{r_2-2}(g(x)-g(y)) \left(\frac{g(x)^{r_1-r_2+1}}{f(x)^{r_1-r_2}} - \frac{g(y)^{r_1 - r_2 + 1}}{f(y)^{r_1 - r_2}} \right). \end{align*}
,
\begin{align*} & |f(x)-f(y)|^{r_2-2}(f(x)-f(y)) \left(\frac{ g(x)^{r_1}}{f(x)^{r_1-1}}-\frac{ g(y)^{r_1}}{f(y)^{r_1-1}} \right) \\ & \quad \le |g(x)-g(y)|^{r_2-2}(g(x)-g(y)) \left(\frac{g(x)^{r_1-r_2+1}}{f(x)^{r_1-r_2}} - \frac{g(y)^{r_1 - r_2 + 1}}{f(y)^{r_1 - r_2}} \right). \end{align*}
(iii) Let $\alpha,\, \beta \ge 1$
 . Then for $x,\,y \in \mathbb {R}^d$
. Then for $x,\,y \in \mathbb {R}^d$ ,
\begin{align*} & |f(x)-f(y)|^{r_1-2}(f(x)-f(y))\\ & \qquad \times \left(\frac{ g(x)^{r_1}}{\alpha f(x)^{r_1-1} + \beta f(x)^{r_2-1}}-\frac{g(y)^{r_1}}{\alpha f(y)^{r_1-1}+\beta f(y)^{r_2-1}} \right) \\ & \quad \le {\mid}{g(x) -g(y)}{\mid}^{r_1}. \end{align*}
,
\begin{align*} & |f(x)-f(y)|^{r_1-2}(f(x)-f(y))\\ & \qquad \times \left(\frac{ g(x)^{r_1}}{\alpha f(x)^{r_1-1} + \beta f(x)^{r_2-1}}-\frac{g(y)^{r_1}}{\alpha f(y)^{r_1-1}+\beta f(y)^{r_2-1}} \right) \\ & \quad \le {\mid}{g(x) -g(y)}{\mid}^{r_1}. \end{align*}
(iv) Let $\alpha,\, \beta \ge 1$
 . Then for $x,\,y \in \mathbb {R}^d$
. Then for $x,\,y \in \mathbb {R}^d$ ,
\begin{align*} & |f(x)-f(y)|^{r_2-2}(f(x)-f(y))\\ & \qquad \times \left(\frac{ g(x)^{r_1}}{\alpha f(x)^{r_1-1} + \beta f(x)^{r_2-1}}-\frac{g(y)^{r_1}}{\alpha f(y)^{r_1-1}+\beta f(y)^{r_2-1}} \right) \\ & \quad \le {\mid}{f(x)^{\frac{r_1}{r_2}}-f(y)^{\frac{r_1}{r_2}}}{\mid}^{r_2}. \end{align*}
,
\begin{align*} & |f(x)-f(y)|^{r_2-2}(f(x)-f(y))\\ & \qquad \times \left(\frac{ g(x)^{r_1}}{\alpha f(x)^{r_1-1} + \beta f(x)^{r_2-1}}-\frac{g(y)^{r_1}}{\alpha f(y)^{r_1-1}+\beta f(y)^{r_2-1}} \right) \\ & \quad \le {\mid}{f(x)^{\frac{r_1}{r_2}}-f(y)^{\frac{r_1}{r_2}}}{\mid}^{r_2}. \end{align*}
Moreover, the equality holds in the above inequalities if and only if $f=cg$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() for some $c \in {\mathbb {R}}$
for some $c \in {\mathbb {R}}$![]() .
.
Proof. For the proof of (i), see [Reference Brasco and Franzina11, Proposition 4.2]. Proof of (ii), (iii), and (iv) follows from [Reference Giacomoni, Gouasmia and Mokrane23, Theorem 2.3 and Remark 2.6].
The following lemma verifies that certain functions are in the fractional Sobolev space, which we require in the subsequent sections.
Lemma 2.4 Let $s \in (0,\,1)$![]() and $r_1,\, r_2 \in (1,\, \infty )$
and $r_1,\, r_2 \in (1,\, \infty )$![]() . Let $u\in W^{s,r_1}_{0}(\Omega )$
. Let $u\in W^{s,r_1}_{0}(\Omega )$![]() be a non-negative function. For $v \in W^{s,r_1}_{0}(\Omega ) \cap L^{\infty }(\Omega )$
be a non-negative function. For $v \in W^{s,r_1}_{0}(\Omega ) \cap L^{\infty }(\Omega )$![]() , the following functions
, the following functions
lie in $W^{s,r_1}_{0}(\Omega )$![]() .
.
Proof. We only prove that $\phi _k \in W^{s,r_1}_{0}(\Omega )$![]() . For other functions, the proof follows using similar arguments. Clearly, $\phi _k$
. For other functions, the proof follows using similar arguments. Clearly, $\phi _k$![]() is in $L^{r_1}(\Omega )$
is in $L^{r_1}(\Omega )$![]() and $\phi _k=0$
and $\phi _k=0$![]() in $\Omega ^c$
in $\Omega ^c$![]() , for every $k.$
, for every $k.$![]() Next, claim that $[\phi _k]_{s,r_1} < \infty$
Next, claim that $[\phi _k]_{s,r_1} < \infty$![]() . In order to show this, for $x,\,y \in \mathbb {R}^d$
. In order to show this, for $x,\,y \in \mathbb {R}^d$![]() , we calculate
, we calculate

Using (iii) of lemma 2.2, we get

Now using $u_k^{-1} \le k$![]() and $v \in L^{\infty }(\Omega )$
and $v \in L^{\infty }(\Omega )$![]() , there exists $C=C(r_1,\,r_2,\,k,\,{\lVert }{v}{\rVert }_{\infty })$
, there exists $C=C(r_1,\,r_2,\,k,\,{\lVert }{v}{\rVert }_{\infty })$![]() such that
such that
Therefore, $\phi _k \in W^{s,r_1}_{0}(\Omega )$![]() follows as $[v]_{s,r_1},\,[u]_{s,r_1}<\infty.$
follows as $[v]_{s,r_1},\,[u]_{s,r_1}<\infty.$![]() This completes the proof.
This completes the proof.
3. Linear independence of the first eigenfunctions
This section is devoted to proving the linear independency of the first Dirichlet eigenfunctions of the fractional $p$![]() -Laplacian and the fractional $q$
-Laplacian and the fractional $q$![]() -Laplacian. Throughout the section, we assume that $\Omega \subset \mathbb {R}^d$
-Laplacian. Throughout the section, we assume that $\Omega \subset \mathbb {R}^d$![]() is a bounded open set of class $C^{1,1}$
is a bounded open set of class $C^{1,1}$![]() . For brevity, we denote the first eigenpair of (2.1) by $(\lambda ^1_{s,r},\,u)$
. For brevity, we denote the first eigenpair of (2.1) by $(\lambda ^1_{s,r},\,u)$![]() . From proposition 2.1, $u>0$
. From proposition 2.1, $u>0$![]() in $\Omega$
in $\Omega$![]() , $u=0$
, $u=0$![]() in $\mathbb {R}^d\setminus \Omega$
in $\mathbb {R}^d\setminus \Omega$![]() and $u \in C(\overline {\Omega })$
and $u \in C(\overline {\Omega })$![]() . Therefore, $u$
. Therefore, $u$![]() attains its maximum in ${\Omega }$
attains its maximum in ${\Omega }$![]() . Due to the translation invariance of the fractional $r$
. Due to the translation invariance of the fractional $r$![]() -Laplacian, we assume that $\Omega$
-Laplacian, we assume that $\Omega$![]() contains the origin and the maximum point for $u$
contains the origin and the maximum point for $u$![]() is the origin. Now for $\tau >0$
is the origin. Now for $\tau >0$![]() , we consider $\Omega _\tau := \{z \in \mathbb {R}^d : \tau z \in \Omega \}$
, we consider $\Omega _\tau := \{z \in \mathbb {R}^d : \tau z \in \Omega \}$![]() and define $u_{\tau } : \mathbb {R}^d \rightarrow {\mathbb {R}}$
and define $u_{\tau } : \mathbb {R}^d \rightarrow {\mathbb {R}}$![]() as follows:
as follows:

The following result demonstrates a property of the above function, which plays an essential role in proving (LI).
Lemma 3.1 (Blow-up lemma)
Let $r \in (1,\, \infty )$![]() and $s \in (0,\,1)$
and $s \in (0,\,1)$![]() . If $\tau _n \to 0$
. If $\tau _n \to 0$![]() , as $n \to \infty$
, as $n \to \infty$![]() , then there exists a subsequence denoted by $(\tau _n)$
, then there exists a subsequence denoted by $(\tau _n)$![]() such that $u_{\tau _n} \to \tilde {u}$
such that $u_{\tau _n} \to \tilde {u}$![]() in $C_{\text {loc}}(\mathbb {R}^d)$
in $C_{\text {loc}}(\mathbb {R}^d)$![]() as $n \to \infty$
as $n \to \infty$![]() . Moreover, $\tilde {u} \in W^{s,r}_{\text {loc}}(\mathbb {R}^d)\cap C(\mathbb {R}^d)$
. Moreover, $\tilde {u} \in W^{s,r}_{\text {loc}}(\mathbb {R}^d)\cap C(\mathbb {R}^d)$![]() is non-negative, and satisfies the following equation weakly:
is non-negative, and satisfies the following equation weakly:
and $\tilde {u}(0) = 0.$![]()
Proof. Note that for any $\tau > 0$![]() , $u_\tau \geq 0$
, $u_\tau \geq 0$![]() , since $u(0)$
, since $u(0)$![]() is the maximum value for $u$
is the maximum value for $u$![]() in $\overline {\Omega }$
in $\overline {\Omega }$![]() . Using the fact that $(\lambda ^1_{s,r},\, u(\tau x))$
. Using the fact that $(\lambda ^1_{s,r},\, u(\tau x))$![]() is the first eigenpair for fractional $r$
is the first eigenpair for fractional $r$![]() -Laplacian on $\Omega _\tau$
-Laplacian on $\Omega _\tau$![]() , we obtain that the following equation holds weakly:
, we obtain that the following equation holds weakly:
For each $\tau >0$![]() , using proposition 2.1 and [Reference Brasco and Parini14, Theorem 3.13], we get $u_{\tau } \in {C}(\Omega _{\tau })$
, using proposition 2.1 and [Reference Brasco and Parini14, Theorem 3.13], we get $u_{\tau } \in {C}(\Omega _{\tau })$![]() . Now we divide our proof into two steps. In the first step, we show that $u_{\tau _n}\to \tilde {u}$
. Now we divide our proof into two steps. In the first step, we show that $u_{\tau _n}\to \tilde {u}$![]() in $C_{\text {loc}}(\mathbb {R}^d)$
in $C_{\text {loc}}(\mathbb {R}^d)$![]() as $n\to \infty$
as $n\to \infty$![]() . In the second step, we prove $\tilde {u}$
. In the second step, we prove $\tilde {u}$![]() is a weak solution to (3.1).
is a weak solution to (3.1).
Step 1: Take a ball $B_R(0)$![]() such that $\overline {B_{4R}(0)}\subset \Omega _\tau$
such that $\overline {B_{4R}(0)}\subset \Omega _\tau$![]() . We choose $\sigma _1>0$
. We choose $\sigma _1>0$![]() as follows
as follows
By the nonlocal Harnack inequality (see [Reference Giacomoni, Kumar and Sreenadh24, Theorem 2.2]), there exists $C=C(d,\,s,\,r)$![]() such that
such that
In (3.3) the last equality follows from the fact $\min _{\substack {B_{2R}(0)}}u_\tau =0$![]() , because origin is the maximum point of $u$
, because origin is the maximum point of $u$![]() in $\Omega$
in $\Omega$![]() . Further, for $r\geq 2$
. Further, for $r\geq 2$![]() we immediately get $(r-1) \sigma _1 > 1$
we immediately get $(r-1) \sigma _1 > 1$![]() , and for $1< r<2$
, and for $1< r<2$![]() we choose
we choose

to get $(r-1)\sigma _1>1$![]() . Then proposition 2.1-(v) and (3.3) yield
. Then proposition 2.1-(v) and (3.3) yield
where $C=C(d,\, s,\, r,\, \lambda ^1_{s,r},\,{\lVert }{u}{\rVert }_{L^{(r-1)\sigma _1}(\mathbb {R}^d)})$![]() . Next, we define the following exponent
. Next, we define the following exponent
Then, applying the regularity estimate [Reference Brasco, Lindgren and Schikorra13, Theorem 1.4] when $r \ge 2$![]() and [Reference Garain and Lindgren22, Theorem 1.2] when $1< r < 2$
and [Reference Garain and Lindgren22, Theorem 1.2] when $1< r < 2$![]() , for the problem (3.2) we get the following Hölder regularity estimate of the weak solution $u_{\tau }$
, for the problem (3.2) we get the following Hölder regularity estimate of the weak solution $u_{\tau }$![]() for any $s<\delta <\Theta (d,\,s,\,r,\,\sigma _1)$
for any $s<\delta <\Theta (d,\,s,\,r,\,\sigma _1)$![]() :
:

where $C=C(d,\,s,\,r)$![]() . We now estimate the last two terms $I_1,\,I_2$
. We now estimate the last two terms $I_1,\,I_2$![]() of (3.6) as follows: Estimate of $I_2$
of (3.6) as follows: Estimate of $I_2$![]() : Choose $a>0$
: Choose $a>0$![]() such that $a >\gamma r-1$
such that $a >\gamma r-1$![]() . Then, by the change of variable we have
. Then, by the change of variable we have

where we see that $r - \frac {1}{\gamma } < \frac {a}{\gamma }$![]() .
.
Estimate of $I_1$![]() : Note that
: Note that

where the last equality follows from the non-negativity of $u_\tau$![]() . To estimate $\mathrm {Tail}_r(u_{\tau }^+;0,\,R)$
. To estimate $\mathrm {Tail}_r(u_{\tau }^+;0,\,R)$![]() , let $R_1 = 4R$
, let $R_1 = 4R$![]() and $\ell :=\max _{\substack {B_{R}(0)}}u_\tau$
and $\ell :=\max _{\substack {B_{R}(0)}}u_\tau$![]() . Take $\phi \in C_c^\infty (B_{R})$
. Take $\phi \in C_c^\infty (B_{R})$![]() satisfying $0\leq \phi \leq 1$
satisfying $0\leq \phi \leq 1$![]() , $\phi =1$
, $\phi =1$![]() in $B_{\frac {R}{2}}$
in $B_{\frac {R}{2}}$![]() and ${\mid }{\nabla \phi }{\mid }\leq \frac {8}{R}$
and ${\mid }{\nabla \phi }{\mid }\leq \frac {8}{R}$![]() . We use the test function $\eta :=(u_\tau -2\ell )\phi ^p$
. We use the test function $\eta :=(u_\tau -2\ell )\phi ^p$![]() in the weak formulation of $u_\tau$
in the weak formulation of $u_\tau$![]() and then proceed similarly as in [Reference T. Kuusi and Palatucci32, Lemma 4.2]) to get a constant $C=C(d,\,s,\,r)$
and then proceed similarly as in [Reference T. Kuusi and Palatucci32, Lemma 4.2]) to get a constant $C=C(d,\,s,\,r)$![]() such that
such that

where in the above estimates we used the fact $|u-2\ell |\leq 3\ell$![]() in $B_{R}$
in $B_{R}$![]() . This implies that
. This implies that

Now, plugging the estimates (3.4), (3.7), (3.8), (3.9) into (3.6), we thus obtain
where $C=C(d,\,s,\,r,\,\lambda ^1_{s,r},\, {\lVert }{u}{\rVert }_{L^{ (r-1) \sigma _1}(\mathbb {R}^d)})$![]() and $\epsilon :=\frac {1}{r-1}(\frac {1+a-r\gamma }{\gamma }) > 0$
and $\epsilon :=\frac {1}{r-1}(\frac {1+a-r\gamma }{\gamma }) > 0$![]() . Let $K \subset \mathbb {R}^d$
. Let $K \subset \mathbb {R}^d$![]() be any compact set. Observe that $\Omega _{\tau }$
be any compact set. Observe that $\Omega _{\tau }$![]() becoming $\mathbb {R}^d$
becoming $\mathbb {R}^d$![]() when $\tau$
when $\tau$![]() is sufficiently small. Thus, we can choose $R>1$
is sufficiently small. Thus, we can choose $R>1$![]() and $0<\tau _0<<1$
and $0<\tau _0<<1$![]() such that $K \subset B_{\frac {R}{8}}(0) \subset \Omega _{\tau }$
such that $K \subset B_{\frac {R}{8}}(0) \subset \Omega _{\tau }$![]() for all $\tau \in (0,\, \tau _0)$
for all $\tau \in (0,\, \tau _0)$![]() . Therefore, we use (3.4) and (3.10) to obtain the following uniform estimate for all $\tau \in (0,\,\tau _0)$
. Therefore, we use (3.4) and (3.10) to obtain the following uniform estimate for all $\tau \in (0,\,\tau _0)$![]() :
:
where $C$![]() is independent of both $\tau$
is independent of both $\tau$![]() and $K$
and $K$![]() . Next, for a sequence $(\tau _n)$
. Next, for a sequence $(\tau _n)$![]() converging to zero, we consider the corresponding sequence of functions $(u_{\tau _n})$
converging to zero, we consider the corresponding sequence of functions $(u_{\tau _n})$![]() . Using (3.11) we can show that $(u_{\tau _n})$
. Using (3.11) we can show that $(u_{\tau _n})$![]() is equicontinuous and uniformly bounded in $K$
is equicontinuous and uniformly bounded in $K$![]() . Therefore, applying the Arzela–Ascoli theorem, up to a subsequence, $u_{\tau _n}\to \tilde {u}\text { in }C(K)$
. Therefore, applying the Arzela–Ascoli theorem, up to a subsequence, $u_{\tau _n}\to \tilde {u}\text { in }C(K)$![]() . Thus we have
. Thus we have
Step 2: Recalling the weak formulation of (3.2) for $\tau >0$![]() be any,
be any,

Let $v\in C_c^\infty (\mathbb {R}^d)$![]() and let $\text {supp}(v) := K$
and let $\text {supp}(v) := K$![]() . Since $\Omega _{\tau _n}$
. Since $\Omega _{\tau _n}$![]() is becoming $\mathbb {R}^d$
is becoming $\mathbb {R}^d$![]() , as $\tau _n\to 0$
, as $\tau _n\to 0$![]() , there exists $n_0 \in \mathbb {N}$
, there exists $n_0 \in \mathbb {N}$![]() such that $K \subset \Omega _{\tau _n}$
such that $K \subset \Omega _{\tau _n}$![]() for all $n\geq n_0.$
for all $n\geq n_0.$![]() Hence, from (3.13) for every $n \ge n_0$
Hence, from (3.13) for every $n \ge n_0$![]() , we write
, we write

We pass the limit as $n\to \infty$![]() in the R.H.S of (3.14), to get
in the R.H.S of (3.14), to get

where the last equality in (3.15) follows using the dominated convergence theorem. Again, applying the dominated convergence theorem, we have

Now, we establish

To show (3.16), for any fixed $k \in \mathbb {N}$![]() we first prove that
we first prove that

It is easy to see from (3.12) that $F_n(x,\,y)\xrightarrow {n\to \infty }F(x,\,y)$![]() pointwise. Now for $x,\,y\in B_k(0)$
pointwise. Now for $x,\,y\in B_k(0)$![]() , and using the uniform boundedness of $(u_{\tau _n})$
, and using the uniform boundedness of $(u_{\tau _n})$![]() (see (3.11)), we have
(see (3.11)), we have

where the constant $C$![]() does not depend on $n$
does not depend on $n$![]() . By Fubini's theorem, we get for any fixed $k\in \mathbb {N}$
. By Fubini's theorem, we get for any fixed $k\in \mathbb {N}$![]()

Thus, applying the dominated convergence theorem, we conclude $F_n \xrightarrow {n\to \infty } F$![]() in $L^1(B_k(0)\times B_k(0))$
in $L^1(B_k(0)\times B_k(0))$![]() . Also, it is easy to verify that for any fixed $n\in \mathbb {N}$
. Also, it is easy to verify that for any fixed $n\in \mathbb {N}$![]()

Again, from the Fatou's lemma, (3.14), and (3.15) we get

Next, for $n,\, k \in \mathbb {N}$![]() , we consider the double sequence of functions $(F_{n,k})$
, we consider the double sequence of functions $(F_{n,k})$![]() defined as
defined as
We claim that

Again, using (3.12), $F_{n,k}(x,\,y)\xrightarrow {n,\,k\to \infty }F(x,\,y)$![]() pointwise a.e. in $\mathbb {R}^d$
pointwise a.e. in $\mathbb {R}^d$![]() . Further, for $x,\,y\in \mathbb {R}^d$
. Further, for $x,\,y\in \mathbb {R}^d$![]() , using the uniform estimate (3.11) we have
, using the uniform estimate (3.11) we have

where the constant $C$![]() is independent of both $n$
is independent of both $n$![]() and $k.$
and $k.$![]() Moreover, from the fact that $\delta > \frac {sr-1}{r-1}$
Moreover, from the fact that $\delta > \frac {sr-1}{r-1}$![]() ,
,

if we choose $\delta < \frac {sr}{r-1}$![]() . Thus, (3.17) follows by again using the dominated convergence theorem. Hence, by the standard result for interchanging double limits, we obtain (3.16). Therefore, taking the limit as $n\to \infty$
. Thus, (3.17) follows by again using the dominated convergence theorem. Hence, by the standard result for interchanging double limits, we obtain (3.16). Therefore, taking the limit as $n\to \infty$![]() in the L.H.S of (3.14) and using (3.16) we obtain
in the L.H.S of (3.14) and using (3.16) we obtain

Thus, using (3.14), (3.15), and (3.18) we get

Moreover, we also have $\tilde {u}\in W^{s,r}_{\text {loc}}(\mathbb {R}^d)\cap C(\mathbb {R}^d)$![]() provided $s<\delta$
provided $s<\delta$![]() . Hence, $\tilde {u}$
. Hence, $\tilde {u}$![]() is a weak solution of (3.1). Again, since $u_{\tau _n}\geq 0$
is a weak solution of (3.1). Again, since $u_{\tau _n}\geq 0$![]() , $u_{\tau _n}(0)=0$
, $u_{\tau _n}(0)=0$![]() , from (3.12) we arrive at $\tilde {u}\geq 0$
, from (3.12) we arrive at $\tilde {u}\geq 0$![]() with $\tilde {u}(0)=0.$
with $\tilde {u}(0)=0.$![]() This completes the proof of the lemma.
This completes the proof of the lemma.
Proof of theorem 1.9.
For simplicity of notation, we denote $u_0 = \phi _{s_1,p}$![]() and $v_0 = \phi _{s_2, q}$
and $v_0 = \phi _{s_2, q}$![]() . We argue by contradiction. Suppose $u_0 = cv_0$
. We argue by contradiction. Suppose $u_0 = cv_0$![]() for some non-zero $c \in {\mathbb {R}}$
for some non-zero $c \in {\mathbb {R}}$![]() . Without loss of any generality, we can assume that $u_0=v_0.$
. Without loss of any generality, we can assume that $u_0=v_0.$![]() By proposition 2.1, $u_0$
By proposition 2.1, $u_0$![]() is uniformly bounded, $u_0>0$
is uniformly bounded, $u_0>0$![]() in $\Omega$
in $\Omega$![]() and is in $C( \overline { \Omega })$
and is in $C( \overline { \Omega })$![]() . This guarantees that $u_0$
. This guarantees that $u_0$![]() has a global extremum point. Since the operator $(-\Delta )_p^{s_1}$
has a global extremum point. Since the operator $(-\Delta )_p^{s_1}$![]() is translation invariant, we can assume that the origin is such a point. Now for $\tau >0$
is translation invariant, we can assume that the origin is such a point. Now for $\tau >0$![]() , define
, define

where $\Omega _\tau :=\{x\in \mathbb {R}^d:\tau x\in \Omega \}$![]() . Then by Blow-up lemma 3.1, there exists a sequence $\tau _n\to 0$
. Then by Blow-up lemma 3.1, there exists a sequence $\tau _n\to 0$![]() such that $u_{\tau _n}\to \tilde {u}$
such that $u_{\tau _n}\to \tilde {u}$![]() in $C_{\text {loc}}(\mathbb {R}^d)$
in $C_{\text {loc}}(\mathbb {R}^d)$![]() , where $\tilde {u}$
, where $\tilde {u}$![]() is a non-negative solution of
is a non-negative solution of
and $\tilde {u}(0)=0.$![]() Again, by the change of variable we deduce
Again, by the change of variable we deduce

This implies that for each $\tau >0$![]() , $u_\tau$
, $u_\tau$![]() given by (3.19) satisfies the following equation weakly
given by (3.19) satisfies the following equation weakly
Using $\frac {s_1{p^{\prime }}}{{q^{\prime }}}< s_2$![]() we again proceed as in Blow-up lemma 3.1, to obtain that $\tilde {u} \ge 0$
we again proceed as in Blow-up lemma 3.1, to obtain that $\tilde {u} \ge 0$![]() is also a weak solution of the following equation:
is also a weak solution of the following equation:
Therefore, by the strong maximum principle [Reference Del P. and Quaas17, Theorem 1.4], we conclude $\tilde {u}=0$![]() a.e. in $\mathbb {R}^d,$
a.e. in $\mathbb {R}^d,$![]() which gives a contradiction to (3.20) as $u_0(0)>0$
which gives a contradiction to (3.20) as $u_0(0)>0$![]() . Thus, the set $\{u_0,\,v_0\}$
. Thus, the set $\{u_0,\,v_0\}$![]() is linearly independent.
is linearly independent.
4. $L^\infty$ bound and maximum principle
bound and maximum principle
In this section, under the presence of multiple exponents $(s_1,\,p),\,(s_2,\,q)$![]() and parameters $(\alpha,\,\beta )$
and parameters $(\alpha,\,\beta )$![]() , we first prove that every nonnegative weak solution of (EV; α, β) is bounded in $\mathbb {R}^d$
, we first prove that every nonnegative weak solution of (EV; α, β) is bounded in $\mathbb {R}^d$![]() . Afterwards, we state a strong maximum principle.
. Afterwards, we state a strong maximum principle.
Theorem 4.1 (Global $L^\infty$ bound)
bound)
Let $0< s_2< s_1<1< q< p<\infty$![]() and let $\Omega \subset \mathbb {R}^d$
and let $\Omega \subset \mathbb {R}^d$![]() be a bounded open set. Assume that $u\in {W_0^{s_1,p}(\Omega )}$
be a bounded open set. Assume that $u\in {W_0^{s_1,p}(\Omega )}$![]() is a nonnegative solution of (EV; α, β). Then $u\in L^{\infty }(\mathbb {R}^d)$
is a nonnegative solution of (EV; α, β). Then $u\in L^{\infty }(\mathbb {R}^d)$![]() .
.
Proof. $\boldsymbol {d>s_1p\,}$![]() : Let $M\geq 0$
: Let $M\geq 0$![]() , define $u_M=\min \{u,\,M\}$
, define $u_M=\min \{u,\,M\}$![]() . Clearly $u_M$
. Clearly $u_M$![]() is non-negative and is in $L^{\infty }(\Omega )$
is non-negative and is in $L^{\infty }(\Omega )$![]() . Since $u\in {W_0^{s_1,p}(\Omega )}$
. Since $u\in {W_0^{s_1,p}(\Omega )}$![]() , then $u_M\in {W_0^{s_1,p}(\Omega )}.$
, then $u_M\in {W_0^{s_1,p}(\Omega )}.$![]() Fixed $\sigma \geq 1$
Fixed $\sigma \geq 1$![]() , define $\phi =u_M^{\sigma }$
, define $\phi =u_M^{\sigma }$![]() . Then, $\phi \in {W_0^{s_1,p}(\Omega )}.$
. Then, $\phi \in {W_0^{s_1,p}(\Omega )}.$![]() Thus taking $\phi$
Thus taking $\phi$![]() as a test function in the weak formulation of $u$
as a test function in the weak formulation of $u$![]() , we have
, we have

Now, using [Reference Brasco, Lindgren and Parini12, Lemma C.2] we estimate

where in the last inequality we use ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^{p^*_{s_1}}(\mathbb {R}^d)$![]() . Since $s_2q < d$
. Since $s_2q < d$![]() , using ${W_0^{s_2,q}(\Omega )} \hookrightarrow L^{q^*_{s_2}}(\mathbb {R}^d)$
, using ${W_0^{s_2,q}(\Omega )} \hookrightarrow L^{q^*_{s_2}}(\mathbb {R}^d)$![]() we estimate $I_2$
we estimate $I_2$![]() as
as

Plugging the estimates of $I_1$![]() and $I_2$
and $I_2$![]() into (4.1) we obtain
into (4.1) we obtain

Letting $M\to \infty$![]() in above, the monotone convergence theorem yields
in above, the monotone convergence theorem yields

Claim For $\sigma _1 := p^*_{s_1} - p +1$![]() , $u^{\sigma _1 + p -1} \in L^{\frac {p^*_{s_1}}{p}}(\mathbb {R}^d)$
, $u^{\sigma _1 + p -1} \in L^{\frac {p^*_{s_1}}{p}}(\mathbb {R}^d)$![]() .
.
By taking $\sigma = \sigma _1$![]() , we obtain from (4.2) that
, we obtain from (4.2) that

Notice that $q+ \sigma _1 -1 = q + p^*_{s_1} -p < p^*_{s_1}$![]() (as $p>q$
(as $p>q$![]() ). Set $a_1:=\frac {p^*_{s_1}}{q+ \sigma _1 -1}$
). Set $a_1:=\frac {p^*_{s_1}}{q+ \sigma _1 -1}$![]() . By applying the Hölder's inequality with conjugate pair $(a_1,\, a_1')$
. By applying the Hölder's inequality with conjugate pair $(a_1,\, a_1')$![]() we estimate the second integral of (4.3) as
we estimate the second integral of (4.3) as

For $R>1$![]() , consider the set $A:= \{ x \in \Omega : u(x) \le R \}$
, consider the set $A:= \{ x \in \Omega : u(x) \le R \}$![]() and $A^c=\Omega \setminus A$
and $A^c=\Omega \setminus A$![]() . We estimate the first integral of the R.H.S of (4.3) as follows:
. We estimate the first integral of the R.H.S of (4.3) as follows:

We choose $R>1$![]() so that
so that

Therefore, combining (4.3), (4.4), and (4.5) we obtain

Thus, $u^{\sigma _1 + p -1} \in L^{\frac {p^*_{s_1}}{p}}(\mathbb {R}^d)$![]() for $\sigma _1 := p^*_{s_1} - p +1$
for $\sigma _1 := p^*_{s_1} - p +1$![]() . Set $a_2:= \frac {p^*_{s_1}+\sigma - 1}{p+\sigma - 1}$
. Set $a_2:= \frac {p^*_{s_1}+\sigma - 1}{p+\sigma - 1}$![]() and $a_3 := \frac {p^*_{s_1}+\sigma - 1}{q+\sigma - 1}$
and $a_3 := \frac {p^*_{s_1}+\sigma - 1}{q+\sigma - 1}$![]() . Using the Young's inequality with the conjugate pairs $(a_2,\,a_2')$
. Using the Young's inequality with the conjugate pairs $(a_2,\,a_2')$![]() and $(a_3,\,a_3')$
and $(a_3,\,a_3')$![]() we write
we write

Hence the R.H.S of (4.2) can be estimated as

Now using the facts $\sigma \ge 1$![]() and $\sigma +p -1 \le \sigma p$
and $\sigma +p -1 \le \sigma p$![]() , we obtain from (4.2) that
, we obtain from (4.2) that

where $C= C(\alpha,\, \beta,\, \Omega,\, d,\,s_1,\,p)>0$![]() . Set $\vartheta =\sigma +p-1$
. Set $\vartheta =\sigma +p-1$![]() . Then the above inequality can be written as
. Then the above inequality can be written as

We consider the sequences $(\vartheta _j)$![]() defined as follows
defined as follows
Observe that $p^*_{s_1}-p+ \vartheta _{j+1} = \frac {p^*_{s_1}}{p} \vartheta _{j}$![]() , and $\vartheta _{j+1} = p + (\frac {p^*_{s_1}}{p})^j(\vartheta _1 - p)$
, and $\vartheta _{j+1} = p + (\frac {p^*_{s_1}}{p})^j(\vartheta _1 - p)$![]() . Since $p^*_{s_1} >p$
. Since $p^*_{s_1} >p$![]() , we get $\vartheta _{j} \rightarrow \infty$
, we get $\vartheta _{j} \rightarrow \infty$![]() , as $j \rightarrow \infty$
, as $j \rightarrow \infty$![]() . From (4.6), we then write
. From (4.6), we then write

Set $D_j := (1+ \int _{\mathbb {R}^d} u(x)^{\frac {p^*_{s_1}}{p}\vartheta _{j}} \, {\rm d}x )^{\frac {p}{p^*_{s_1}(\vartheta _{j}-p)}}.$![]() We iterate (4.7) to get
We iterate (4.7) to get

where $D_1 = (1+ \int _{\mathbb {R}^d} u(x)^{\frac {p^*_{s_1}}{p}p^*_{s_1}} \, {\rm d}x )^{\frac {p}{p^*_{s_1}(p^*_{s_1}-p)}}$![]() which is finite by using the claim, and
which is finite by using the claim, and

Combining (4.8) and (4.9) we have

Moreover,

Therefore, taking the limit as $j \rightarrow \infty$![]() in (4.10), we conclude that $u \in L^{\infty }(\mathbb {R}^d)$
in (4.10), we conclude that $u \in L^{\infty }(\mathbb {R}^d)$![]() .
.
$\boldsymbol {d=s_1p\,}$![]() : We proceed similarly as in the previous case by replacing the following fractional Sobolev inequality (whenever required):
: We proceed similarly as in the previous case by replacing the following fractional Sobolev inequality (whenever required):

where
Following similar arguments as given in the case $d>s_1p$![]() , we infer
, we infer

Then by considering the following sequences $(\vartheta _j)$![]() defined as:
defined as:
we obtain $u \in L^{\infty }(\mathbb {R}^d)$![]() .
.
$\boldsymbol {d< s_1p\,}$![]() : By the fractional Morrey's inequality ([Reference Brasco, Lindgren and Parini12, Proposition 2.9]), we see that functions in ${W_0^{s_1,p}(\Omega )}$
: By the fractional Morrey's inequality ([Reference Brasco, Lindgren and Parini12, Proposition 2.9]), we see that functions in ${W_0^{s_1,p}(\Omega )}$![]() are Hölder continuous and hence bounded. This completes the proof.
are Hölder continuous and hence bounded. This completes the proof.
We use the following version of the strong maximum principle for the positive solution of (EV; α, β).
Proposition 4.2 (Strong Maximum Principle)
Let $\Omega \subset \mathbb {R}^d$![]() be a bounded open set and $0< s_2< s_1<1< q< p< \infty$
be a bounded open set and $0< s_2< s_1<1< q< p< \infty$![]() . Let $u \in {W_0^{s_1,p}(\Omega )}\cap L^\infty (\mathbb {R}^d)$
. Let $u \in {W_0^{s_1,p}(\Omega )}\cap L^\infty (\mathbb {R}^d)$![]() be a non-negative supersolution of (EV; α, β). Then either $u>0$
be a non-negative supersolution of (EV; α, β). Then either $u>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() or $u \equiv 0$
or $u \equiv 0$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() .
.
Proof. $\boldsymbol {\alpha,\, \beta \ge 0}$![]() : Since $u$
: Since $u$![]() is a non-negative supersolution of (EV; α, β), we obtain
is a non-negative supersolution of (EV; α, β), we obtain
for every $v \in {W_0^{s_1,p}(\Omega )}$![]() with $v \ge 0$
with $v \ge 0$![]() . Now we can use [Reference Ambrosio3, (2) of Theorem 1.1] (by taking $c(x)=0$
. Now we can use [Reference Ambrosio3, (2) of Theorem 1.1] (by taking $c(x)=0$![]() ) with modifications (due to the presence of multiple parameters $s_1,\,s_2$
) with modifications (due to the presence of multiple parameters $s_1,\,s_2$![]() ) to conclude either $u>0$
) to conclude either $u>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() or $u \equiv 0$
or $u \equiv 0$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() .
.
$\boldsymbol {\alpha,\, \beta \le 0}$![]() or $\boldsymbol {\alpha \beta \leq 0}$
or $\boldsymbol {\alpha \beta \leq 0}$![]() : Let $x_0 \in \Omega$
: Let $x_0 \in \Omega$![]() and $R>0$
and $R>0$![]() be such that $B_R(x_0) \subset \Omega$
be such that $B_R(x_0) \subset \Omega$![]() . Since $u$
. Since $u$![]() is a non-negative supersolution of (EV; α, β), then we proceed as in [Reference Ambrosio3, Lemma 2.1], for any $R_1 > 0$
is a non-negative supersolution of (EV; α, β), then we proceed as in [Reference Ambrosio3, Lemma 2.1], for any $R_1 > 0$![]() satisfying $B_{R_1} = B_{R_1}(x_0) \subset B_{\frac {R}{2}}(x_0)$
satisfying $B_{R_1} = B_{R_1}(x_0) \subset B_{\frac {R}{2}}(x_0)$![]() , and obtain the following logarithmic estimate
, and obtain the following logarithmic estimate

where $\delta \in (0,\,1)$![]() and $C= C(d,\,s_1,\,p,\,s_2,\,q)>0$
and $C= C(d,\,s_1,\,p,\,s_2,\,q)>0$![]() . Now the result follows using (4.12) and the arguments given in [Reference Ambrosio3, Lemma 2.3].
. Now the result follows using (4.12) and the arguments given in [Reference Ambrosio3, Lemma 2.3].
5. Variational framework
To obtain the existence part of theorem 1.2–1.7, in this section, we study several properties of energy functionals associated with (EV; α, β). In view of remark 1.8, we assume $s_2 < s_1$![]() and $q < p$
and $q < p$![]() in the rest of the paper. We consider the following functional on ${W_0^{s_1,p}(\Omega )}$
in the rest of the paper. We consider the following functional on ${W_0^{s_1,p}(\Omega )}$![]() :
:
Now we define

where $\left < \cdot \right >$![]() denotes the duality action. Using the Hölder's inequality, it follows that ${\lVert }{A_p(u)}{\rVert } \le [u]_{s_1, p}^{p-1}$
denotes the duality action. Using the Hölder's inequality, it follows that ${\lVert }{A_p(u)}{\rVert } \le [u]_{s_1, p}^{p-1}$![]() and ${\lVert }{B_q(u)}{\rVert } \le [u]_{s_2, q}^{q-1}$
and ${\lVert }{B_q(u)}{\rVert } \le [u]_{s_2, q}^{q-1}$![]() . One can verify that $I_+ \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$
. One can verify that $I_+ \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$![]() and
and

Remark 5.1 If $u \in {W_0^{s_1,p}(\Omega )}$![]() is a critical point of $I_+$
is a critical point of $I_+$![]() , i.e., $\big < I_+'(u),\, \phi \big > =0$
, i.e., $\big < I_+'(u),\, \phi \big > =0$![]() for all $\phi \in {W_0^{s_1,p}(\Omega )}$
for all $\phi \in {W_0^{s_1,p}(\Omega )}$![]() , then $u$
, then $u$![]() is a solution of (EV; α, β). Moreover, for $\phi =-u^{-}$
is a solution of (EV; α, β). Moreover, for $\phi =-u^{-}$![]() , using (i) of lemma 2.2 we see
, using (i) of lemma 2.2 we see
The above inequality yields $u^{-} = c$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() for some $c\in \mathbb {R}$
for some $c\in \mathbb {R}$![]() . Moreover, since $u^{-}\in {W_0^{s_1,p}(\Omega )}$
. Moreover, since $u^{-}\in {W_0^{s_1,p}(\Omega )}$![]() , we get $c=0$
, we get $c=0$![]() . Thus every critical point of $I_+$
. Thus every critical point of $I_+$![]() is a nonnegative solution of (EV; α, β).
is a nonnegative solution of (EV; α, β).
Now we discuss the coercivity and weak lower semicontinuity of $I_+$![]() .
.
Proposition 5.2 Let $\alpha < \lambda _{s_1,p}^1$![]() and $\beta >0$
and $\beta >0$![]() . Then the functional $I_+$
. Then the functional $I_+$![]() is weakly sequentially lower semicontinuous, coercive, and bounded below on ${W_0^{s_1,p}(\Omega )}$
is weakly sequentially lower semicontinuous, coercive, and bounded below on ${W_0^{s_1,p}(\Omega )}$![]() .
.
Proof. Let $u_n \rightharpoonup u$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Then using the compactness of the embeddings ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$
. Then using the compactness of the embeddings ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$![]() , ${W_0^{s_2,q}(\Omega )} \hookrightarrow L^{q}(\Omega )$
, ${W_0^{s_2,q}(\Omega )} \hookrightarrow L^{q}(\Omega )$![]() , and the weak lower semicontinuity of the seminorm, we get
, and the weak lower semicontinuity of the seminorm, we get

Now we prove the coercivity of $I_+$![]() . Suppose $\alpha \le 0$
. Suppose $\alpha \le 0$![]() . Then using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^q(\Omega )$
. Then using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^q(\Omega )$![]() ,
,
If $\alpha > 0$![]() , then there exists $a \in (0,\,1)$
, then there exists $a \in (0,\,1)$![]() such that $\alpha = a \lambda _{s_1,p}^1$
such that $\alpha = a \lambda _{s_1,p}^1$![]() . In this case, using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^q(\Omega )$
. In this case, using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^q(\Omega )$![]() , we get
, we get
for every $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$![]() . From the definition of $\lambda _{s_1,p}^1$
. From the definition of $\lambda _{s_1,p}^1$![]() , we have $[u]_{s_1,p}^p \ge \lambda _{s_1,p}^1 {\lVert }{u}{\rVert }_p^p \ge \lambda _{s_1,p}^1 {\lVert }{u^+}{\rVert }_p^p$
, we have $[u]_{s_1,p}^p \ge \lambda _{s_1,p}^1 {\lVert }{u}{\rVert }_p^p \ge \lambda _{s_1,p}^1 {\lVert }{u^+}{\rVert }_p^p$![]() . Therefore, (5.1) yields
. Therefore, (5.1) yields
In view of (5.1), observe that (5.3) holds for every $\alpha < \lambda _{s_1,p}^1$![]() . For any $\epsilon >0$
. For any $\epsilon >0$![]() , applying Young's inequality with the conjugate pair $(\frac {p}{q},\, \frac {p}{p-q})$
, applying Young's inequality with the conjugate pair $(\frac {p}{q},\, \frac {p}{p-q})$![]() we obtain
we obtain
Hence from (5.1) we have the following estimate for every $u \in {W_0^{s_1,p}(\Omega )} \setminus \{ 0\}$![]() :
:
We choose $\epsilon >0$![]() so that $C \beta \epsilon < \frac {1-a}{2}$
so that $C \beta \epsilon < \frac {1-a}{2}$![]() . Therefore, from the above estimate, we get
. Therefore, from the above estimate, we get
Thus the functional $I_+$![]() is coercive on ${W_0^{s_1,p}(\Omega )}$
is coercive on ${W_0^{s_1,p}(\Omega )}$![]() . Next, we prove that $I_+$
. Next, we prove that $I_+$![]() is bounded below. Set $M>0$
is bounded below. Set $M>0$![]() such that $M^{p-q} \ge p(1+C \beta q^{-1})$
such that $M^{p-q} \ge p(1+C \beta q^{-1})$![]() . Then using (5.1), we get
. Then using (5.1), we get
Further, if $[u]_{s_1,p} \le M$![]() , then $I_+(u) \ge - \frac { M^q C \beta }{q}$
, then $I_+(u) \ge - \frac { M^q C \beta }{q}$![]() . Thus, $I_+$
. Thus, $I_+$![]() is bounded below on ${W_0^{s_1,p}(\Omega )}$
is bounded below on ${W_0^{s_1,p}(\Omega )}$![]() .
.
In the following proposition, we verify that $I_+$![]() satisfies the Palais–Smale (P.S.) condition on ${W_0^{s_1,p}(\Omega )}$
satisfies the Palais–Smale (P.S.) condition on ${W_0^{s_1,p}(\Omega )}$![]() .
.
Proposition 5.3 Let $\alpha \neq \lambda ^1_{s_1,p}$![]() . Let $(u_n)$
. Let $(u_n)$![]() be a sequence in ${W_0^{s_1,p}(\Omega )}$
be a sequence in ${W_0^{s_1,p}(\Omega )}$![]() such that $I_+(u_n) \rightarrow c$
such that $I_+(u_n) \rightarrow c$![]() for some $c \in {\mathbb {R}}$
for some $c \in {\mathbb {R}}$![]() and $I_+'(u_n) \rightarrow 0$
and $I_+'(u_n) \rightarrow 0$![]() in $({W_0^{s_1,p}(\Omega )})^*$
in $({W_0^{s_1,p}(\Omega )})^*$![]() . Then $(u_n)$
. Then $(u_n)$![]() possesses a convergent subsequence in ${W_0^{s_1,p}(\Omega )}$
possesses a convergent subsequence in ${W_0^{s_1,p}(\Omega )}$![]() .
.
Proof. First, we show that the sequence $(u_n)$![]() is bounded in ${W_0^{s_1,p}(\Omega )}$
is bounded in ${W_0^{s_1,p}(\Omega )}$![]() . On a contrary, assume that $[u_n]_{s_1,p} \rightarrow \infty$
. On a contrary, assume that $[u_n]_{s_1,p} \rightarrow \infty$![]() , as $n \rightarrow \infty$
, as $n \rightarrow \infty$![]() . Using (i) of lemma 2.2, note that
. Using (i) of lemma 2.2, note that
Hence $[u_n^-]_{s_1, p} \rightarrow 0$![]() , as $n \rightarrow \infty$
, as $n \rightarrow \infty$![]() . Set $w_n=u_n [u_n]_{s_1,p}^{-1}$
. Set $w_n=u_n [u_n]_{s_1,p}^{-1}$![]() . Up to a subsequence, $w_n \rightharpoonup w$
. Up to a subsequence, $w_n \rightharpoonup w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() and by the compactness of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$
and by the compactness of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$![]() , $w_n \rightarrow w$
, $w_n \rightarrow w$![]() in $L^p(\Omega )$
in $L^p(\Omega )$![]() . Further, $[w_n^-]_{s_1,p} = [u_n^-]_{s_1,p} [u_n]_{s_1,p}^{-1} \rightarrow 0$
. Further, $[w_n^-]_{s_1,p} = [u_n^-]_{s_1,p} [u_n]_{s_1,p}^{-1} \rightarrow 0$![]() , as $n \rightarrow \infty$
, as $n \rightarrow \infty$![]() . Therefore, $w_n^- \rightarrow 0$
. Therefore, $w_n^- \rightarrow 0$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() and hence in $L^p(\Omega )$
and hence in $L^p(\Omega )$![]() . This implies that $w_n^+ \rightarrow w$
. This implies that $w_n^+ \rightarrow w$![]() in $L^p(\Omega )$
in $L^p(\Omega )$![]() , which yields $w \ge 0$
, which yields $w \ge 0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . We show that $w$
. We show that $w$![]() is an eigenfunction of the fractional $p$
is an eigenfunction of the fractional $p$![]() -Laplacian corresponding to $\alpha$
-Laplacian corresponding to $\alpha$![]() . For any $\phi \in {W_0^{s_1,p}(\Omega )}$
. For any $\phi \in {W_0^{s_1,p}(\Omega )}$![]() , we write
, we write
where $\epsilon _n \rightarrow 0$![]() as $n \rightarrow \infty$
as $n \rightarrow \infty$![]() . From the above inequality, we obtain
. From the above inequality, we obtain

Using the Hölder's inequality with the conjugate pair $(q,\, q')$![]() , the Poincaré inequality ${\lVert }{\phi }{\rVert }_q \le C(\Omega ) [\phi ]_{s_1,p}$
, the Poincaré inequality ${\lVert }{\phi }{\rVert }_q \le C(\Omega ) [\phi ]_{s_1,p}$![]() , and the boundedness of $(w_n)$
, and the boundedness of $(w_n)$![]() in ${W_0^{s_2,q}(\Omega )}$
in ${W_0^{s_2,q}(\Omega )}$![]() we have
we have

We choose $\phi =w_n-w$![]() in (5.5), and take the limit as $n \rightarrow \infty$
in (5.5), and take the limit as $n \rightarrow \infty$![]() to get $\left < A_p(w_n),\, w_n-w\right > \rightarrow 0.$
to get $\left < A_p(w_n),\, w_n-w\right > \rightarrow 0.$![]() Further, since $A_p$
Further, since $A_p$![]() is a continuous functional on ${W_0^{s_1,p}(\Omega )}$
is a continuous functional on ${W_0^{s_1,p}(\Omega )}$![]() , we also have $\left < A_p(w),\, w_n-w\right > \rightarrow 0$
, we also have $\left < A_p(w),\, w_n-w\right > \rightarrow 0$![]() . Further, using the definition of $A_p$
. Further, using the definition of $A_p$![]()
Therefore, $[w_n]_{s_1,p} \rightarrow [w]_{s_1,p}$![]() , and hence the uniform convexity of ${W_0^{s_1,p}(\Omega )}$
, and hence the uniform convexity of ${W_0^{s_1,p}(\Omega )}$![]() ensures that $w_n \rightarrow w$
ensures that $w_n \rightarrow w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Further, since $[w]_{s_1,p}=1$
. Further, since $[w]_{s_1,p}=1$![]() we also have $w \neq 0$
we also have $w \neq 0$![]() in $\Omega$
in $\Omega$![]() . Now using (5.5), we obtain
. Now using (5.5), we obtain
Thus $w$![]() is a nonnegative weak solution to the problem
is a nonnegative weak solution to the problem
Now by the strong maximum principle for fractional $p$![]() -Laplacian [Reference Brasco and Parini14, Proposition 2.6], we conclude that $w>0$
-Laplacian [Reference Brasco and Parini14, Proposition 2.6], we conclude that $w>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Therefore, the uniqueness of $\lambda ^1_{s_1,p}$
. Therefore, the uniqueness of $\lambda ^1_{s_1,p}$![]() (proposition 2.1) yields $\alpha = \lambda ^1_{s_1,p}$
(proposition 2.1) yields $\alpha = \lambda ^1_{s_1,p}$![]() , resulting in a contradiction. Thus, the sequence $(u_n)$
, resulting in a contradiction. Thus, the sequence $(u_n)$![]() is bounded in ${W_0^{s_1,p}(\Omega )}$
is bounded in ${W_0^{s_1,p}(\Omega )}$![]() . By the reflexivity, up to a subsequence, $u_n \rightharpoonup \tilde {u}$
. By the reflexivity, up to a subsequence, $u_n \rightharpoonup \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . By taking $\phi =u_n-\tilde {u}$
. By taking $\phi =u_n-\tilde {u}$![]() in (5.4) and using the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^{\gamma }(\Omega )$
in (5.4) and using the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^{\gamma }(\Omega )$![]() with $\gamma \in [1,\,p]$
with $\gamma \in [1,\,p]$![]() , we get $\left < A_p(u_n),\, u_n-\tilde {u} \right > + \left < B_q(u_n),\, u_n - \tilde {u} \right > \rightarrow 0$
, we get $\left < A_p(u_n),\, u_n-\tilde {u} \right > + \left < B_q(u_n),\, u_n - \tilde {u} \right > \rightarrow 0$![]() . Therefore, $\left < A_p(u_n)- A_p(\tilde {u}),\, u_n-\tilde {u} \right > + \left < B_q(u_n)- B_q(\tilde {u}),\, u_n - \tilde {u} \right > \rightarrow 0$
. Therefore, $\left < A_p(u_n)- A_p(\tilde {u}),\, u_n-\tilde {u} \right > + \left < B_q(u_n)- B_q(\tilde {u}),\, u_n - \tilde {u} \right > \rightarrow 0$![]() , which implies $\left < A_p(u_n)- A_p(\tilde {u}),\, u_n-\tilde {u} \right >\to 0$
, which implies $\left < A_p(u_n)- A_p(\tilde {u}),\, u_n-\tilde {u} \right >\to 0$![]() . Thus, $[u_n]_{s_1,p} \rightarrow [\tilde {u}]_{s_1,p}$
. Thus, $[u_n]_{s_1,p} \rightarrow [\tilde {u}]_{s_1,p}$![]() (by using (5.6)), and from the uniform convexity, $u_n \rightarrow \tilde {u}$
(by using (5.6)), and from the uniform convexity, $u_n \rightarrow \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() , as required.
, as required.
The following lemma discusses the mountain pass geometry of $I_+$![]() for certain ranges of $\alpha$
for certain ranges of $\alpha$![]() and $\beta$
and $\beta$![]() .
.
Lemma 5.4 Let $\alpha > \lambda ^1_{s_1,p}$![]() and $\beta \le \alpha$
and $\beta \le \alpha$![]() . For $\rho >0$
. For $\rho >0$![]() , let
, let
The following hold:
(i) There exist $\delta = \delta (\rho )>0$
 , and $\alpha _1 =\alpha _1(\rho )>0$
, and $\alpha _1 =\alpha _1(\rho )>0$ such that if $\alpha \in (0,\, \alpha _1)$
such that if $\alpha \in (0,\, \alpha _1)$ , then $I_+(u) \ge \delta$
, then $I_+(u) \ge \delta$ for every $u\in \mathbb {S}_{\rho }$
for every $u\in \mathbb {S}_{\rho }$ .
.(ii) There exists $v \in {W_0^{s_1,p}(\Omega )}$
 with $[v]_{s_1,p} > \rho$
with $[v]_{s_1,p} > \rho$ such that $I_+(v)<0$
such that $I_+(v)<0$ .
.
Proof. (i) Let $\rho >0$![]() and $u \in \mathbb {S}_{\rho }$
and $u \in \mathbb {S}_{\rho }$![]() . Then using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^\gamma (\Omega )$
. Then using ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^\gamma (\Omega )$![]() for $\gamma \in [1,\,p]$
for $\gamma \in [1,\,p]$![]() ,
,

where $A(\rho )=\frac {\rho ^{p-q}}{p} - C \alpha \frac {\rho ^{p-q}}{p} - C\frac {\alpha }{q}$![]() . Choose $0 < \alpha _1 < \frac {\rho ^{p-q}}{p} ( C\frac {\rho ^{p-q}}{p} + \frac {C}{q} )^{-1}$
. Choose $0 < \alpha _1 < \frac {\rho ^{p-q}}{p} ( C\frac {\rho ^{p-q}}{p} + \frac {C}{q} )^{-1}$![]() and $\delta = \rho ^{q} A(\rho )$
and $\delta = \rho ^{q} A(\rho )$![]() with $\alpha \in (0,\, \alpha _1)$
with $\alpha \in (0,\, \alpha _1)$![]() . Therefore, from (5.8), $I_+(u) \ge \delta$
. Therefore, from (5.8), $I_+(u) \ge \delta$![]() for all $\alpha \in (0,\, \alpha _1)$
for all $\alpha \in (0,\, \alpha _1)$![]() . (ii) Note that
. (ii) Note that
Since $p > q$![]() and $\alpha > \lambda ^1_{s_1,p}$
and $\alpha > \lambda ^1_{s_1,p}$![]() , we obtain $I_+(t\phi _{s_1,p}) \rightarrow -\infty$
, we obtain $I_+(t\phi _{s_1,p}) \rightarrow -\infty$![]() , as $t \rightarrow \infty$
, as $t \rightarrow \infty$![]() . Hence there exists $t_1 > \rho [\phi _{s_1,p}]_{s_1,p}^{-1}$
. Hence there exists $t_1 > \rho [\phi _{s_1,p}]_{s_1,p}^{-1}$![]() such that $I_+(t\phi _{s_1,p})<0$
such that $I_+(t\phi _{s_1,p})<0$![]() for all $t \ge t_1$
for all $t \ge t_1$![]() . Thus, $v=t\phi _{s_1,p}$
. Thus, $v=t\phi _{s_1,p}$![]() with $t>t_1$
with $t>t_1$![]() is the required function.
is the required function.
5.1 Nehari manifold
This subsection briefly discusses the Nehari manifold associated with (EV; α, β) and some of its properties.
Definition 5.5 Nehari Manifold
We define the Nehari manifold associated with (EV; α, β) as
Note that every nonnegative solution of (EV; α, β) lies in $\mathcal {N}_{\alpha, \beta }$![]() . Now we provide a sufficient condition for which every critical point in ${\mathcal {N}}_{\alpha, \beta }$
. Now we provide a sufficient condition for which every critical point in ${\mathcal {N}}_{\alpha, \beta }$![]() becomes a nonnegative solution of (EV; α, β). We consider the following functionals on ${W_0^{s_1,p}(\Omega )}$
becomes a nonnegative solution of (EV; α, β). We consider the following functionals on ${W_0^{s_1,p}(\Omega )}$![]() :
:
Clearly, $H_{\alpha },\, G_{\beta } \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$![]() , and the identity $\left < I_+'(u),\, u\right > = H_{\alpha }(u) + G_{\beta }(u)$
, and the identity $\left < I_+'(u),\, u\right > = H_{\alpha }(u) + G_{\beta }(u)$![]() holds.
holds.
Proposition 5.6 Let $u \in {W_0^{s_1,p}(\Omega )}$![]() . Assume that either $H_{\alpha }(u) \neq 0$
. Assume that either $H_{\alpha }(u) \neq 0$![]() or $G_{\beta }(u) \neq 0$
or $G_{\beta }(u) \neq 0$![]() . If $u$
. If $u$![]() is a critical point in ${\mathcal {N}}_{\alpha, \beta }$
is a critical point in ${\mathcal {N}}_{\alpha, \beta }$![]() , then $u$
, then $u$![]() is a critical point of $I_+$
is a critical point of $I_+$![]() .
.
Proof. The proof follows using the arguments given in [Reference Bobkov and Tanaka8, Lemma 2].
Next, we state a condition for the existence of a critical point in ${\mathcal {N}}_{\alpha, \beta }$![]() . Let $H_{\alpha }(u),\,G_{\beta }(u) \neq 0$
. Let $H_{\alpha }(u),\,G_{\beta }(u) \neq 0$![]() for some $u \in {W_0^{s_1,p}(\Omega )}$
for some $u \in {W_0^{s_1,p}(\Omega )}$![]() . Define
. Define

Notice that, for $t \in {\mathbb {R}}$![]() , $\left < I'(t u),\, tu \right > = t (t^{p-1}H_{\alpha }(u) + t^{q-1}G_{\beta }(u))$
, $\left < I'(t u),\, tu \right > = t (t^{p-1}H_{\alpha }(u) + t^{q-1}G_{\beta }(u))$![]() . In particular, $t_{\alpha,\beta }u \in {\mathcal {N}}_{\alpha, \beta }$
. In particular, $t_{\alpha,\beta }u \in {\mathcal {N}}_{\alpha, \beta }$![]() .
.
Proposition 5.7 Let $u \in {W_0^{s_1,p}(\Omega )}$![]() . The following hold:
. The following hold:
(i) If $G_{\beta }(u)<0< H_{\alpha }(u)$
 , then $I_+(t_{\alpha,\beta }u)= \underset {t \in {\mathbb {R}}^+}{\min } I_+(tu)$
, then $I_+(t_{\alpha,\beta }u)= \underset {t \in {\mathbb {R}}^+}{\min } I_+(tu)$ , and $I_+(t_{\alpha,\beta }u)<0$
, and $I_+(t_{\alpha,\beta }u)<0$ . Moreover, $t_{\alpha,\beta }$
. Moreover, $t_{\alpha,\beta }$ is unique.
is unique.(ii) If $H_{\alpha }(u) < 0 < G_{\beta }(u)$
 , then $I_+(t_{\alpha,\beta }u)= \underset {t \in {\mathbb {R}}^+}{\max } \, I_+(tu)$
, then $I_+(t_{\alpha,\beta }u)= \underset {t \in {\mathbb {R}}^+}{\max } \, I_+(tu)$ , and $I_+(t_{\alpha,\beta }u)>0$
, and $I_+(t_{\alpha,\beta }u)>0$ . Moreover, $t_{\alpha,\beta }$
. Moreover, $t_{\alpha,\beta }$ is unique.
is unique.
Proof. The proof follows using the same arguments presented in [Reference Bobkov and Tanaka8, Proposition 6].
Remark 5.8
(i) Let $u \in {\mathcal {N}}_{\alpha, \beta }$
 . Then $H_{\alpha }(u) + G_{\beta }(u) =0$
. Then $H_{\alpha }(u) + G_{\beta }(u) =0$ , and hence
\[ I_+(u)= \frac{p-q}{pq}G_{\beta}(u)= \frac{q-p}{pq} H_{\alpha}(u). \]From the above identity, it is clear that if $I_+(u) \neq 0$
, and hence
\[ I_+(u)= \frac{p-q}{pq}G_{\beta}(u)= \frac{q-p}{pq} H_{\alpha}(u). \]From the above identity, it is clear that if $I_+(u) \neq 0$
 , then either $G_{\beta }(u)<0< H_{\alpha }(u)$
, then either $G_{\beta }(u)<0< H_{\alpha }(u)$ or $H_{\alpha }(u) < 0 < G_{\beta }(u)$
or $H_{\alpha }(u) < 0 < G_{\beta }(u)$ .
.(ii) If $u \in {\mathcal {N}}_{\alpha,\beta }$
 , and $H_{\alpha },\, G_{\beta }$
, and $H_{\alpha },\, G_{\beta }$ satisfy the assumptions given in the above proposition, then from (i) and proposition 5.7, $t_{\alpha,\beta } = 1$
satisfy the assumptions given in the above proposition, then from (i) and proposition 5.7, $t_{\alpha,\beta } = 1$ is the unique minimum or maximum point on ${\mathbb {R}}^+$
is the unique minimum or maximum point on ${\mathbb {R}}^+$ .
.
Remark 5.9 Using proposition 2.1 and ${\lVert }{u^+}{\rVert }_{\gamma } \le {\lVert }{u}{\rVert }_{\gamma }$![]() , we get
, we get
(i) if $\alpha < \lambda _{s_1,p}^1$
 , then $H_{\alpha }(u) > [u]_{s_1,p}^p - \lambda _{s_1,p}^1 {\lVert }{u^+}{\rVert }^p_p \ge [u]_{s_1,p}^p - \lambda _{s_1,p}^1 {\lVert }{u}{\rVert }^p_p \ge 0$
, then $H_{\alpha }(u) > [u]_{s_1,p}^p - \lambda _{s_1,p}^1 {\lVert }{u^+}{\rVert }^p_p \ge [u]_{s_1,p}^p - \lambda _{s_1,p}^1 {\lVert }{u}{\rVert }^p_p \ge 0$ for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$ ,
,(ii) if $\beta < \lambda _{s_2,q}^1$
 , then $G_{\beta }(u) > [u]_{s_1,p}^p - \lambda _{s_2,q}^1 {\lVert }{u^+}{\rVert }^q_q \ge [u]_{s_2,q}^q - \lambda _{s_2,q}^1 {\lVert }{u}{\rVert }^q_q \ge 0$
, then $G_{\beta }(u) > [u]_{s_1,p}^p - \lambda _{s_2,q}^1 {\lVert }{u^+}{\rVert }^q_q \ge [u]_{s_2,q}^q - \lambda _{s_2,q}^1 {\lVert }{u}{\rVert }^q_q \ge 0$ for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$ .
.
5.2 Method of sub and super solutions
We consider the following energy functional on ${W_0^{s_1,p}(\Omega )}$![]() :
:
Notice that $I \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$![]() , and
, and

In this subsection, using sub and super solutions techniques, we discuss the existence of critical points for $I$![]() . We say $\overline {u} \in {W_0^{s_1,p}(\Omega )}$
. We say $\overline {u} \in {W_0^{s_1,p}(\Omega )}$![]() is a supersolution of (EV; α, β), if
is a supersolution of (EV; α, β), if

A function $\underline {u} \in {W_0^{s_1,p}(\Omega )}$![]() is called a subsolution of (EV; α, β) if the reverse inequality holds in (5.9).
is called a subsolution of (EV; α, β) if the reverse inequality holds in (5.9).
Definition 5.10 Truncation function
Let $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$![]() be such that $\underline {u} \le \overline {u}$
be such that $\underline {u} \le \overline {u}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . For $t \in {\mathbb {R}}$
. For $t \in {\mathbb {R}}$![]() , we define the truncation function corresponds to $f(t)= \alpha {\mid }{t}{\mid }^{p-2}t + \beta {\mid }{t}{\mid }^{q-2}t$
, we define the truncation function corresponds to $f(t)= \alpha {\mid }{t}{\mid }^{p-2}t + \beta {\mid }{t}{\mid }^{q-2}t$![]() as follows:
as follows:

By definition, $\tilde {f}(\cdot,\, t)$![]() is continuous on ${\mathbb {R}}$
is continuous on ${\mathbb {R}}$![]() . Further, using $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$
. Further, using $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$![]() it is easy to see that $\tilde {f} \in L^{\infty }(\Omega \times {\mathbb {R}})$
it is easy to see that $\tilde {f} \in L^{\infty }(\Omega \times {\mathbb {R}})$![]() . Now we consider the following functional associated with $\tilde {f}(\cdot,\, u(x))$
. Now we consider the following functional associated with $\tilde {f}(\cdot,\, u(x))$![]() :
:
where $\tilde {F}( x,\, u(x)) := \int _0^{u(x)} \tilde {f} (x,\, \tau ) \, {\rm d}\tau$![]() . Note that, for $u(x) \in (\underline {u}(x),\, \overline {u}(x))$
. Note that, for $u(x) \in (\underline {u}(x),\, \overline {u}(x))$![]() , $\tilde {I}$
, $\tilde {I}$![]() coincides with the energy functional $I$
coincides with the energy functional $I$![]() . Further, $\tilde {I} \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$
. Further, $\tilde {I} \in C^1({W_0^{s_1,p}(\Omega )},\, {\mathbb {R}})$![]() , and
, and
In the following proposition, we prove some properties of $\tilde {I}$![]() that ensure the existence of critical points for $\tilde {I}$
that ensure the existence of critical points for $\tilde {I}$![]() .
.
Proposition 5.11 Let $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$![]() be such that $\underline {u} \le \overline {u}$
be such that $\underline {u} \le \overline {u}$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() . Then $\tilde {I}$
. Then $\tilde {I}$![]() is bounded below, coercive and weak lower semicontinuous on ${W_0^{s_1,p}(\Omega )}$
is bounded below, coercive and weak lower semicontinuous on ${W_0^{s_1,p}(\Omega )}$![]() .
.
Proof. Since $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$![]() , there exists $C>0$
, there exists $C>0$![]() such that ${\mid }{\tilde {f}(x,\,t)}{\mid } \le C$
such that ${\mid }{\tilde {f}(x,\,t)}{\mid } \le C$![]() , and ${\mid }{\tilde {F}(x,\,t)}{\mid } \le C|t|$
, and ${\mid }{\tilde {F}(x,\,t)}{\mid } \le C|t|$![]() , for all $x\in \Omega,\, t \in {\mathbb {R}}$
, for all $x\in \Omega,\, t \in {\mathbb {R}}$![]() . Hence for $u \in {W_0^{s_1,p}(\Omega )}$
. Hence for $u \in {W_0^{s_1,p}(\Omega )}$![]()
Now using similar arguments as in proposition 5.2, it follows that $\tilde {I}$![]() is coercive and bounded below on ${W_0^{s_1,p}(\Omega )}$
is coercive and bounded below on ${W_0^{s_1,p}(\Omega )}$![]() . Next, for a sequence $u_n \rightharpoonup u$
. Next, for a sequence $u_n \rightharpoonup u$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() ,
,
We claim that $\int _{\Omega } \tilde {F}(x,\,u_n(x)) \, {\rm d}x \rightarrow \int _{\Omega } \tilde {F}(x,\,u(x)) \, {\rm d}x$![]() . By the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$
. By the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^p(\Omega )$![]() , we have $u_n \rightarrow u$
, we have $u_n \rightarrow u$![]() in $L^p(\Omega )$
in $L^p(\Omega )$![]() and hence $u_n \rightarrow u$
and hence $u_n \rightarrow u$![]() in $L^1(\Omega )$
in $L^1(\Omega )$![]() . Further, using $\tilde {f} \in L^{\infty }(\Omega \times {\mathbb {R}} )$
. Further, using $\tilde {f} \in L^{\infty }(\Omega \times {\mathbb {R}} )$![]() ,
,

and the claim follows. Therefore, in view of (5.11), $\tilde {I}$![]() is weak lower semicontinuous on ${W_0^{s_1,p}(\Omega )}$
is weak lower semicontinuous on ${W_0^{s_1,p}(\Omega )}$![]() .
.
In the following proposition, we prove that every critical point of $\tilde {I}$![]() lies between sub and super solutions.
lies between sub and super solutions.
Proposition 5.12 Let $\underline {u},\, \overline {u} \in L^{\infty }(\Omega )$![]() be such that $\underline {u} \le \overline {u}$
be such that $\underline {u} \le \overline {u}$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() . If $u \in {W_0^{s_1,p}(\Omega )}$
. If $u \in {W_0^{s_1,p}(\Omega )}$![]() is a critical point of $\tilde {I}$
is a critical point of $\tilde {I}$![]() , then $\underline {u} \le u \le \overline {u}$
, then $\underline {u} \le u \le \overline {u}$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() .
.
Proof. From the definition of sub and super solutions, it is clear that $\underline {u} = u = \overline {u} =0$![]() in $\mathbb {R}^d \setminus \Omega$
in $\mathbb {R}^d \setminus \Omega$![]() , since each function lies in ${W_0^{s_1,p}(\Omega )}$
, since each function lies in ${W_0^{s_1,p}(\Omega )}$![]() . Now we show that $\underline {u} \le u \le \overline {u}$
. Now we show that $\underline {u} \le u \le \overline {u}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Our proof is by the method of contradiction. On the contrary, assume that $u \ge \overline {u}$
. Our proof is by the method of contradiction. On the contrary, assume that $u \ge \overline {u}$![]() on $A \subset \Omega$
on $A \subset \Omega$![]() with $|A| >0$
with $|A| >0$![]() . We choose $(u - \overline {u})^+ \in {W_0^{s_1,p}(\Omega )}$
. We choose $(u - \overline {u})^+ \in {W_0^{s_1,p}(\Omega )}$![]() as a test function. Using $\overline {u}$
as a test function. Using $\overline {u}$![]() is a supersolution of (EV; α, β) and $u$
is a supersolution of (EV; α, β) and $u$![]() is a critical point of $\tilde {I}$
is a critical point of $\tilde {I}$![]() , together with (5.10) we get
, together with (5.10) we get

The above inequalities yield
From the definition of $A_p$![]() ,
,

Now we consider the following cases:
$\boldsymbol {2 \le q < p}$![]() : Without loss of generality, we assume that $u(x) -\overline {u}(x) \ge u(y)- \overline {u}(y)$
: Without loss of generality, we assume that $u(x) -\overline {u}(x) \ge u(y)- \overline {u}(y)$![]() . Otherwise, exchange the roll of $x$
. Otherwise, exchange the roll of $x$![]() and $y$
and $y$![]() . Applying (ii) and (i) of lemma 2.2, we then obtain
. Applying (ii) and (i) of lemma 2.2, we then obtain

Similarly, we can show that $\big < B_q(u)-B_q(\overline {u}),\, (u-\overline {u})^+ \big > \ge C(q)[(u-\overline {u})^+]^q_{s_2,q}$![]() . Therefore, from (5.12), $[(u-\overline {u})^+]_{s_1,p} = 0$
. Therefore, from (5.12), $[(u-\overline {u})^+]_{s_1,p} = 0$![]() . By Poincarè inequality, ${\lVert }{(u-\overline {u})^+}{\rVert }_p \le C[(u-\overline {u})^+]_{s_1,p}= 0$
. By Poincarè inequality, ${\lVert }{(u-\overline {u})^+}{\rVert }_p \le C[(u-\overline {u})^+]_{s_1,p}= 0$![]() , which is a contradiction.
, which is a contradiction.
$\boldsymbol {q < 2 \le p}$![]() : In this case, using [Reference Iannizzotto, Mosconi and Squassina28, Lemma 2.4] (for $B_q$
: In this case, using [Reference Iannizzotto, Mosconi and Squassina28, Lemma 2.4] (for $B_q$![]() ) we obtain,
) we obtain,

Hence, we get a contradiction using (5.12). For $q < p < 2$![]() , again using [Reference Iannizzotto, Mosconi and Squassina28, Lemma 2.4], we similarly get a contradiction. Thus $u \le \overline {u}$
, again using [Reference Iannizzotto, Mosconi and Squassina28, Lemma 2.4], we similarly get a contradiction. Thus $u \le \overline {u}$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() . Now suppose $u \le \underline {u}$
. Now suppose $u \le \underline {u}$![]() in $A \subset \Omega$
in $A \subset \Omega$![]() with $|A| > 0$
with $|A| > 0$![]() , then taking $(u-\underline {u})^- \in {W_0^{s_1,p}(\Omega )}$
, then taking $(u-\underline {u})^- \in {W_0^{s_1,p}(\Omega )}$![]() as a test function, we also get a contradiction for all possible choices of $p$
as a test function, we also get a contradiction for all possible choices of $p$![]() and $q$
and $q$![]() . Therefore, $\underline {u} \le u \le \overline {u}$
. Therefore, $\underline {u} \le u \le \overline {u}$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() .
.
6. Existence and non-existence of positive solutions
Depending on the ranges of $\alpha,\, \beta$![]() , this section is devoted to proving the existence and non-existence of positive solutions for (EV; α, β). This section's terminology ‘solution’ is meant to be nontrivial unless otherwise specified. First, we consider the region where $\alpha,\, \beta$
, this section is devoted to proving the existence and non-existence of positive solutions for (EV; α, β). This section's terminology ‘solution’ is meant to be nontrivial unless otherwise specified. First, we consider the region where $\alpha,\, \beta$![]() do not exceed $\lambda _{s_1,p}^1,\, \lambda _{s_2,q}^1$
do not exceed $\lambda _{s_1,p}^1,\, \lambda _{s_2,q}^1$![]() respectively.
respectively.
Proposition 6.1 It holds
(i) Let $(\alpha,\,\beta ) \in ((-\infty,\, \lambda _{s_1,p}^1) \times (-\infty,\, \lambda _{s_2,q}^1)) \cup ( \{\lambda _{s_1,p}^1\} \times (-\infty,\, \lambda _{s_2,q}^1) ) \cup ( (-\infty, \lambda _{s_1,p}^1) \times \{\lambda _{s_2,q}^1\} )$
 . Then (EV; α, β) does not admit a solution.
. Then (EV; α, β) does not admit a solution.(ii) Let $\alpha = \lambda _{s_1,p}^1$
 and $\beta = \lambda _{s_2,q}^1$
and $\beta = \lambda _{s_2,q}^1$ . Then (EV; α, β) admits a solution if and only if (LI) violates.
. Then (EV; α, β) admits a solution if and only if (LI) violates.
Proof. (i) Let $\alpha < \lambda _{s_1,p}^1$![]() and $\beta < \lambda _{s_2,q}^1$
and $\beta < \lambda _{s_2,q}^1$![]() . Suppose $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
. Suppose $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$![]() is a solution of (EV; α, β). Then using the definition of $\lambda _{s_1,p}^1$
is a solution of (EV; α, β). Then using the definition of $\lambda _{s_1,p}^1$![]() and $\lambda _{s_2,q}^1$
and $\lambda _{s_2,q}^1$![]() (proposition 2.1), we get
(proposition 2.1), we get
A contradiction. Therefore, (EV; α, β) does not admit a solution. For other cases, contradiction similarly follows using (6.1). (ii) For $\alpha = \lambda _{s_1,p}^1$![]() and $\beta = \lambda _{s_2,q}^1$
and $\beta = \lambda _{s_2,q}^1$![]() , if $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
, if $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$![]() is a solution of (EV; α, β), then the equality occurs in (6.1). As a consequence, $u$
is a solution of (EV; α, β), then the equality occurs in (6.1). As a consequence, $u$![]() becomes an eigenfunction corresponding to both $\lambda _{s_1,p}^1$
becomes an eigenfunction corresponding to both $\lambda _{s_1,p}^1$![]() and $\lambda _{s_2,q}^1$
and $\lambda _{s_2,q}^1$![]() , i.e., (LI) violates. Conversely, suppose (LI) does not hold. For $\alpha \le \lambda _{s_1,p}^1$
, i.e., (LI) violates. Conversely, suppose (LI) does not hold. For $\alpha \le \lambda _{s_1,p}^1$![]() and $\beta \le \lambda _{s_2,q}^1$
and $\beta \le \lambda _{s_2,q}^1$![]() , using remark 5.9 we have $I_+(u) \ge 0$
, using remark 5.9 we have $I_+(u) \ge 0$![]() for any $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
for any $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$![]() . Thus $0$
. Thus $0$![]() is the global minimizing point for $I_+$
is the global minimizing point for $I_+$![]() . Further, since $\phi _{s_1,p} = c\phi _{s_2,q}$
. Further, since $\phi _{s_1,p} = c\phi _{s_2,q}$![]() for some nonzero $c \in {\mathbb {R}}$
for some nonzero $c \in {\mathbb {R}}$![]() , by setting $\tilde {u}=c_1\phi _{s_1,p} = c_2\phi _{s_2,q}$
, by setting $\tilde {u}=c_1\phi _{s_1,p} = c_2\phi _{s_2,q}$![]() (where $c_1,\, c_2 \neq 0$
(where $c_1,\, c_2 \neq 0$![]() ) we see that $I_+(\tilde {u})=0$
) we see that $I_+(\tilde {u})=0$![]() . Therefore, $\tilde {u} \neq 0$
. Therefore, $\tilde {u} \neq 0$![]() is a solution of (EV; α, β).
is a solution of (EV; α, β).
Before going to the proof of theorem 1.2, we recall a result from [Reference Nguyen and Vo30], where for $d>s_1p$![]() the authors provided the existence of a positive solution of (1.3). However, we stress that the same conclusion can be drawn for ${\rm d}\leq s_1p$
the authors provided the existence of a positive solution of (1.3). However, we stress that the same conclusion can be drawn for ${\rm d}\leq s_1p$![]() . For $0< s<1\le r< \infty$
. For $0< s<1\le r< \infty$![]() and $m_r \in L^{\infty }(\Omega )$
and $m_r \in L^{\infty }(\Omega )$![]() with $m_r^+ \not \equiv 0$
with $m_r^+ \not \equiv 0$![]() , we denote
, we denote
as the first Dirichlet eigenvalue of the weighted eigenvalue problem of the fractional $r$![]() -Laplace operator (see [Reference Del P. and Quaas16]).
-Laplace operator (see [Reference Del P. and Quaas16]).
Theorem 6.2 [Reference Nguyen and Vo30, Theorem 1.1]
Let $\Omega \subset \mathbb {R}^d$![]() be a bounded open set, $0< s_2< s_1< 1< q \le p< \infty$
be a bounded open set, $0< s_2< s_1< 1< q \le p< \infty$![]() , and $m_p,\, m_q \in L^{\infty }(\Omega )$
, and $m_p,\, m_q \in L^{\infty }(\Omega )$![]() with $m_p^+,\, m_q^+ \not \equiv 0$
with $m_p^+,\, m_q^+ \not \equiv 0$![]() . Let $\lambda _{s_1,p}^1(\Omega,\,m_p),\, \lambda _{s_2,q}^1(\Omega,\,m_q)$
. Let $\lambda _{s_1,p}^1(\Omega,\,m_p),\, \lambda _{s_2,q}^1(\Omega,\,m_q)$![]() be respectively the first Dirichlet eigenvalue of weighted eigenvalue problems for fractional $p$
be respectively the first Dirichlet eigenvalue of weighted eigenvalue problems for fractional $p$![]() -Laplace and fractional $q$
-Laplace and fractional $q$![]() -Laplace operators with weights $m_p,\, m_q$
-Laplace operators with weights $m_p,\, m_q$![]() . Suppose, $\lambda _{s_1,p}^1(\Omega,\, m_p) \neq \lambda _{s_2,q}^1(\Omega,\, m_q)$
. Suppose, $\lambda _{s_1,p}^1(\Omega,\, m_p) \neq \lambda _{s_2,q}^1(\Omega,\, m_q)$![]() . Then for
. Then for
the problem (1.3) admits a positive solution.
Proof of theorem 1.2. (i) $\boldsymbol {\alpha > \lambda _{s_1,p}^1,\,\beta < \lambda _{s_2,q}^1\,}$![]() : Let $\beta > 0$
: Let $\beta > 0$![]() . Then using $\alpha > \lambda _{s_1,p}^1$
. Then using $\alpha > \lambda _{s_1,p}^1$![]() and $\beta < \lambda _{s_2,q}^1$
and $\beta < \lambda _{s_2,q}^1$![]() , we get
, we get
Hence $\beta > \min \{ \lambda _{s_1,p}^1 (\Omega,\, \frac {\alpha }{\beta }),\, \lambda _{s_2,q}^1(\Omega,\,1) \}$![]() and using theorem 6.2 with $m_p = \frac {\alpha }{\beta }$
and using theorem 6.2 with $m_p = \frac {\alpha }{\beta }$![]() and $m_q=1$
and $m_q=1$![]() we obtain that (EV; α, β) admits a positive solution. Let $\beta \le 0$
we obtain that (EV; α, β) admits a positive solution. Let $\beta \le 0$![]() . Then using proposition 5.3 and lemma 5.4, $I_+$
. Then using proposition 5.3 and lemma 5.4, $I_+$![]() satisfies all the conditions of the Mountain pass theorem (see [Reference Ambrosetti and Rabinowitz1, Theorem 2.1]). Therefore, by the Mountain pass theorem and remark 5.1, (EV; α, β) admits a nonnegative and nontrivial solution $u \in {W_0^{s_1,p}(\Omega )}$
satisfies all the conditions of the Mountain pass theorem (see [Reference Ambrosetti and Rabinowitz1, Theorem 2.1]). Therefore, by the Mountain pass theorem and remark 5.1, (EV; α, β) admits a nonnegative and nontrivial solution $u \in {W_0^{s_1,p}(\Omega )}$![]() . Further, from the strong maximum principle (proposition 4.3), $u >0$
. Further, from the strong maximum principle (proposition 4.3), $u >0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
$\boldsymbol {\alpha < \lambda _{s_1,p}^1,\,\beta > \lambda _{s_2,q}^1\,}$![]() : Let $\alpha >0$
: Let $\alpha >0$![]() . Then using $\alpha < \lambda _{s_1,p}^1$
. Then using $\alpha < \lambda _{s_1,p}^1$![]() and $\beta > \lambda _{s_2,q}^1$
and $\beta > \lambda _{s_2,q}^1$![]() , we get $\lambda _{s_2,q}^1(\Omega,\, \frac {\beta }{\alpha })< \alpha < \lambda _{s_1,p}^1(\Omega,\,1)$
, we get $\lambda _{s_2,q}^1(\Omega,\, \frac {\beta }{\alpha })< \alpha < \lambda _{s_1,p}^1(\Omega,\,1)$![]() . Therefore, theorem 6.2 with $m_p=1$
. Therefore, theorem 6.2 with $m_p=1$![]() and $m_q=\frac {\beta }{\alpha }$
and $m_q=\frac {\beta }{\alpha }$![]() yields a positive solution for (EV; α, β). If $\alpha \le 0$
yields a positive solution for (EV; α, β). If $\alpha \le 0$![]() , then from proposition 5.2, we get the existence of a global minimizer $\tilde {u}$
, then from proposition 5.2, we get the existence of a global minimizer $\tilde {u}$![]() of $I_+$
of $I_+$![]() , and hence using remark 5.1, $\tilde {u}$
, and hence using remark 5.1, $\tilde {u}$![]() is a nonnegative solution of (EV; α, β). Next, we show that $\tilde {u} \neq 0$
is a nonnegative solution of (EV; α, β). Next, we show that $\tilde {u} \neq 0$![]() in $\Omega$
in $\Omega$![]() . Observe that, for $t>0$
. Observe that, for $t>0$![]() , $G_{\beta }(t\phi _{s_2,q}) = t^q G_{\beta }(\phi _{s_2,q})<0$
, $G_{\beta }(t\phi _{s_2,q}) = t^q G_{\beta }(\phi _{s_2,q})<0$![]() , and using remark 5.9, $H_{\alpha }(t\phi _{s_2,q}) = t^p H_{\alpha }(\phi _{s_2,q})>0$
, and using remark 5.9, $H_{\alpha }(t\phi _{s_2,q}) = t^p H_{\alpha }(\phi _{s_2,q})>0$![]() . Now, if $0< t << 1$
. Now, if $0< t << 1$![]() , then $I_+(t\phi _{s_2,q})<0$
, then $I_+(t\phi _{s_2,q})<0$![]() , which implies that $I_+(\tilde {u})<0$
, which implies that $I_+(\tilde {u})<0$![]() and $\tilde {u} \neq 0$
and $\tilde {u} \neq 0$![]() . Therefore, by the strong maximum principle (proposition 4.3), $\tilde {u}>0$
. Therefore, by the strong maximum principle (proposition 4.3), $\tilde {u}>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
$\boldsymbol {\alpha = \lambda _{s_1,p}^1,\,\beta = \lambda _{s_2,q}^1\,}$![]() : Let (LI) violates. Then using (ii) of proposition 6.1, we see that (EV; α, β) admits a nonnegative solution $u \in {W_0^{s_1,p}(\Omega )}$
: Let (LI) violates. Then using (ii) of proposition 6.1, we see that (EV; α, β) admits a nonnegative solution $u \in {W_0^{s_1,p}(\Omega )}$![]() . Further, using the strong maximum principle (proposition 4.3), $u>0$
. Further, using the strong maximum principle (proposition 4.3), $u>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
(ii) Suppose, there exists nonzero $c \in {\mathbb {R}}$![]() such that $\phi _{s_1,p}=c\phi _{s_2,q}$
such that $\phi _{s_1,p}=c\phi _{s_2,q}$![]() . We also assume that (EV; α, β) admits a solution $u >0$
. We also assume that (EV; α, β) admits a solution $u >0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Using the Picone's inequality ((i) of lemma 2.3) and proposition 2.1, we get
. Using the Picone's inequality ((i) of lemma 2.3) and proposition 2.1, we get

Since for $x,\,y \in \mathbb {R}^d$![]() , $u_k(x)-u_k(y)=u(x)-u(y)$
, $u_k(x)-u_k(y)=u(x)-u(y)$![]() the above inequality yields
the above inequality yields

We again use the Picone's inequality ((ii) of lemma 2.3) to obtain

Since $\phi _{s_1,p} \in L^{\infty }(\Omega )$![]() ((v) of proposition 2.1), using lemma 2.4, $u_k^{q-p}\phi _{s_1,p}^{p-q+1} \in {W_0^{s_1,p}(\Omega )}$
((v) of proposition 2.1), using lemma 2.4, $u_k^{q-p}\phi _{s_1,p}^{p-q+1} \in {W_0^{s_1,p}(\Omega )}$![]() . Therefore, we have the following identity:
. Therefore, we have the following identity:

Set $f_k := u_k^{q-p}\phi _{s_1,p}^p$![]() and $f:=u^{q-p}\phi _{s_1,p}^p$
and $f:=u^{q-p}\phi _{s_1,p}^p$![]() . It is easy to see that $f_k$
. It is easy to see that $f_k$![]() is increasing and $f_k \in L^1(\Omega )$
is increasing and $f_k \in L^1(\Omega )$![]() . Moreover, for $\gamma \le p$
. Moreover, for $\gamma \le p$![]() , using $u_k(x)^{\gamma -p} \rightarrow u(x)^{\gamma -p}$
, using $u_k(x)^{\gamma -p} \rightarrow u(x)^{\gamma -p}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() , we get $f_k(x) \rightarrow f(x)$
, we get $f_k(x) \rightarrow f(x)$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Therefore, the monotone convergence theorem yields $f \in L^1(\Omega )$
. Therefore, the monotone convergence theorem yields $f \in L^1(\Omega )$![]() , and $\int _{\Omega } f_k(x) \, {\rm d}x \rightarrow \int _{\Omega } f(x) \, {\rm d}x$
, and $\int _{\Omega } f_k(x) \, {\rm d}x \rightarrow \int _{\Omega } f(x) \, {\rm d}x$![]() , as $k \rightarrow \infty$
, as $k \rightarrow \infty$![]() . Hence from (6.3) and (6.4), we obtain
. Hence from (6.3) and (6.4), we obtain

Now since $u$![]() is a solution of (EV; α, β), taking $u_k^{1-p}\phi _{s_1,p}^{p} \in {W_0^{s_1,p}(\Omega )}$
is a solution of (EV; α, β), taking $u_k^{1-p}\phi _{s_1,p}^{p} \in {W_0^{s_1,p}(\Omega )}$![]() (by (v) of proposition 2.1, and lemma 2.4) as a test function,
(by (v) of proposition 2.1, and lemma 2.4) as a test function,

Furthermore, for $\gamma \in (1,\,p]$![]() , the Hölder's inequality with the conjugate pair $(\gamma,\,\gamma ')$
, the Hölder's inequality with the conjugate pair $(\gamma,\,\gamma ')$![]() yields,
yields,
Moreover, $\frac {u^{\gamma -1}}{u_k^{p-1}} \phi _{s_1,p}^p \rightarrow u^{\gamma -p} \phi _{s_1,p}^p$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() , and the sequence $(u_k^{1-p})$
, and the sequence $(u_k^{1-p})$![]() is increasing. Hence, again applying the monotone convergence theorem
is increasing. Hence, again applying the monotone convergence theorem
Therefore, (6.2), (6.5) and (6.6) yield

The above inequality infer that, $(\alpha,\, \beta ) \in ((\lambda _{s_1,p}^1,\, \infty ) \times (-\infty,\, \lambda _{s_2,q}^1)) \cup ((-\infty,\, \lambda _{s_1,p}^1) \times (\lambda _{s_2,q}^1,\,\infty )) \cup ( \{\lambda _{s_1,p}^1\} \times \{\lambda _{s_2,q}^1\} )$![]() . This completes our proof.
. This completes our proof.
Now we proceed to prove the existence and non-existence of positive solution for (EV; α, β) on the line $\beta = \lambda _{s_2,q}^1$![]() . Recall the following quantity:
. Recall the following quantity:

Notice that, $\alpha ^*_{s_1,p} \ge \lambda _{s_1,p}^1$![]() and if (LI) holds, then $\alpha ^*_{s_1,p} > \lambda _{s_1,p}^1$
and if (LI) holds, then $\alpha ^*_{s_1,p} > \lambda _{s_1,p}^1$![]() . In the rest of this section, we assume that the condition (LI) holds. The following lemma states that if $\alpha$
. In the rest of this section, we assume that the condition (LI) holds. The following lemma states that if $\alpha$![]() is smaller than $\alpha ^*_{s_1,p}$
is smaller than $\alpha ^*_{s_1,p}$![]() , then $H_{\alpha }$
, then $H_{\alpha }$![]() and $G_{\beta }$
and $G_{\beta }$![]() possess a different sign on ${\mathcal {N}}_{\alpha, \beta }$
possess a different sign on ${\mathcal {N}}_{\alpha, \beta }$![]() .
.
Lemma 6.3 Let $\beta = \lambda _{s_2,q}^1$![]() and $\alpha < \alpha ^*_{s_1,p}$
and $\alpha < \alpha ^*_{s_1,p}$![]() . Then $H_{\alpha }(u) < 0< G_{\beta }(u)$
. Then $H_{\alpha }(u) < 0< G_{\beta }(u)$![]() for every $u \in {\mathcal {N}}_{\alpha, \beta }$
for every $u \in {\mathcal {N}}_{\alpha, \beta }$![]() .
.
Proof. Notice that, $G_{\beta }(u) = [u]^q_{s_2,q} - \lambda _{s_2,q}^1 {\lVert }{u^+}{\rVert }_q^q \ge [u]^q_{s_2,q} - \lambda _{s_2,q}^1 {\lVert }{u}{\rVert }_q^q \ge 0$![]() for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$
for $u \in {W_0^{s_1,p}(\Omega )} \setminus \{0\}$![]() . Let $u \in {\mathcal {N}}_{\alpha, \beta }$
. Let $u \in {\mathcal {N}}_{\alpha, \beta }$![]() . If $G_{\beta }(u) = 0$
. If $G_{\beta }(u) = 0$![]() , then we get
, then we get

By the simplicity of $\lambda _{s_2,q}^1$![]() ((iv) of proposition 2.1), $u=c\phi _{s_2,q}$
((iv) of proposition 2.1), $u=c\phi _{s_2,q}$![]() for some $c \in {\mathbb {R}}$
for some $c \in {\mathbb {R}}$![]() . Hence
. Hence
On the other hand, since $u \in {\mathcal {N}}_{\alpha, \beta }$![]() , $H_{\alpha }(u) = - G_{\beta }(u) = 0$
, $H_{\alpha }(u) = - G_{\beta }(u) = 0$![]() , a contradiction. Therefore, we must have $G_{\beta }(u) >0$
, a contradiction. Therefore, we must have $G_{\beta }(u) >0$![]() . Further, since $u \in {\mathcal {N}}_{\alpha, \beta }$
. Further, since $u \in {\mathcal {N}}_{\alpha, \beta }$![]() , we obtain $H_{\alpha }(u)<0< G_{\beta }(u)$
, we obtain $H_{\alpha }(u)<0< G_{\beta }(u)$![]() .
.
Now we are ready to prove the existence and non-existence of positive solution for $\beta = \lambda _{s_2,q}^1$![]() .
.
Proposition 6.4 For $\beta = \lambda _{s_2,q}^1$![]() the following hold:
the following hold:
Proof. (i) We show that $d := \min \{I_+(u): u \in {\mathcal {N}}_{\alpha, \beta }\}$![]() is attained. Let $(u_n)$
is attained. Let $(u_n)$![]() be the minimizing sequence in ${\mathcal {N}}_{\alpha,\beta }$
be the minimizing sequence in ${\mathcal {N}}_{\alpha,\beta }$![]() , i.e., $\big < I_+'(u_n),\,u_n\big >=0$
, i.e., $\big < I_+'(u_n),\,u_n\big >=0$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() and $I_+(u_n) \rightarrow d$
and $I_+(u_n) \rightarrow d$![]() as $n \rightarrow \infty$
as $n \rightarrow \infty$![]() . From lemma 6.3, $H_{\alpha }(u_n) < 0 < G_{\beta }(u_n)$
. From lemma 6.3, $H_{\alpha }(u_n) < 0 < G_{\beta }(u_n)$![]() . Step 1: This step proves the boundedness of $(u_n)$
. Step 1: This step proves the boundedness of $(u_n)$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . On a contrary, suppose $[u_n]_{s_1,p} \rightarrow \infty$
. On a contrary, suppose $[u_n]_{s_1,p} \rightarrow \infty$![]() , as $n \rightarrow \infty$
, as $n \rightarrow \infty$![]() . Set $w_n = u_n [u_n]_{s_1,p}^{-1}$
. Set $w_n = u_n [u_n]_{s_1,p}^{-1}$![]() . By the reflexivity, $w_n \rightharpoonup w$
. By the reflexivity, $w_n \rightharpoonup w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() and $w_n \rightarrow w$
and $w_n \rightarrow w$![]() in $L^p(\Omega )$
in $L^p(\Omega )$![]() . Since $H_{\alpha }(u_n) < 0$
. Since $H_{\alpha }(u_n) < 0$![]() , we have ${\lVert }{w_n}{\rVert }_p^p = {\lVert }{u_n}{\rVert }_p^p [u_n]^{-p}_{s_1,p} > \frac {1}{\alpha }$
, we have ${\lVert }{w_n}{\rVert }_p^p = {\lVert }{u_n}{\rVert }_p^p [u_n]^{-p}_{s_1,p} > \frac {1}{\alpha }$![]() . This gives ${\lVert }{w}{\rVert }_p^p \ge \frac {1}{\alpha }$
. This gives ${\lVert }{w}{\rVert }_p^p \ge \frac {1}{\alpha }$![]() , and hence $w \neq 0$
, and hence $w \neq 0$![]() . Now using (i) of remark 5.8,
. Now using (i) of remark 5.8,
Using (6.8) we obtain
Therefore, $w = c\phi _{s_2,q}$![]() for some $c \in {\mathbb {R}}$
for some $c \in {\mathbb {R}}$![]() . Further, using (i) of remark 5.8, and (6.8),
. Further, using (i) of remark 5.8, and (6.8),
The above inequality yields $\alpha ^*_{s_1,p} \le \alpha$![]() , a contradiction. Therefore, $(u_n)$
, a contradiction. Therefore, $(u_n)$![]() must be bounded in ${W_0^{s_1,p}(\Omega )}$
must be bounded in ${W_0^{s_1,p}(\Omega )}$![]() . Step 2: By the reflexivity, $u_n \rightharpoonup \tilde {u}$
. Step 2: By the reflexivity, $u_n \rightharpoonup \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . In this step, we show $(u_n)$
. In this step, we show $(u_n)$![]() converges to $\tilde {u}$
converges to $\tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . On a contrary, suppose $[u_n]_{s_1,p} \not \rightarrow [\tilde {u}]_{s_1,p}$
. On a contrary, suppose $[u_n]_{s_1,p} \not \rightarrow [\tilde {u}]_{s_1,p}$![]() . If $\lim _{n \rightarrow \infty } [u_n]_{s_1,p} < [\tilde {u}]_{s_1,p}$
. If $\lim _{n \rightarrow \infty } [u_n]_{s_1,p} < [\tilde {u}]_{s_1,p}$![]() , then $\mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } [u_n]_{s_1,p} < [\tilde {u}]_{s_1,p}$
, then $\mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } [u_n]_{s_1,p} < [\tilde {u}]_{s_1,p}$![]() contradicts the weak lower semicontinuity of $[\cdot ]_{s_1,p}$
contradicts the weak lower semicontinuity of $[\cdot ]_{s_1,p}$![]() . Henceforth, assume that $[\tilde {u}]_{s_1,p} < \lim _{n \rightarrow \infty } [u_n]_{s_1,p}$
. Henceforth, assume that $[\tilde {u}]_{s_1,p} < \lim _{n \rightarrow \infty } [u_n]_{s_1,p}$![]() . Using this inequality we get $[\tilde {u}]_{s_1,p} < \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } [u_n]_{s_1,p}$
. Using this inequality we get $[\tilde {u}]_{s_1,p} < \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } [u_n]_{s_1,p}$![]() and $H_{\alpha }(\tilde {u}) < \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } H_{\alpha }(u_n) \le 0$
and $H_{\alpha }(\tilde {u}) < \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } H_{\alpha }(u_n) \le 0$![]() . This implies that $\tilde {u}$
. This implies that $\tilde {u}$![]() is nonzero. Now, $G_{\beta }(\tilde {u}) \ge 0$
is nonzero. Now, $G_{\beta }(\tilde {u}) \ge 0$![]() , and if $G_{\beta }(\tilde {u})=0$
, and if $G_{\beta }(\tilde {u})=0$![]() , then $\tilde {u}=c\phi _{s_2,q}$
, then $\tilde {u}=c\phi _{s_2,q}$![]() for some $c \in {\mathbb {R}}$
for some $c \in {\mathbb {R}}$![]() . Hence $H_{\alpha }(\phi _{s_2,q}) <0$
. Hence $H_{\alpha }(\phi _{s_2,q}) <0$![]() which implies that $\alpha > \alpha ^*_{s_1,p}$
which implies that $\alpha > \alpha ^*_{s_1,p}$![]() , a contradiction. Therefore, $H_{\alpha }(\tilde {u}) < 0 < G_{\beta }(\tilde {u})$
, a contradiction. Therefore, $H_{\alpha }(\tilde {u}) < 0 < G_{\beta }(\tilde {u})$![]() . Now applying proposition 5.7 there exists a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$
. Now applying proposition 5.7 there exists a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$![]() such that $t_{\alpha,\beta }\tilde {u} \in {\mathcal {N}}_{\alpha, \beta }$
such that $t_{\alpha,\beta }\tilde {u} \in {\mathcal {N}}_{\alpha, \beta }$![]() and $0< I_+(t_{\alpha,\beta } \tilde {u})= \max _{t \in {\mathbb {R}}^+} \, I_+(t\tilde {u})$
and $0< I_+(t_{\alpha,\beta } \tilde {u})= \max _{t \in {\mathbb {R}}^+} \, I_+(t\tilde {u})$![]() . Moreover, from (ii) of remark 5.8, $I_+(u_n)= \max _{t \in {\mathbb {R}}^+} \, I_+(tu_n)$
. Moreover, from (ii) of remark 5.8, $I_+(u_n)= \max _{t \in {\mathbb {R}}^+} \, I_+(tu_n)$![]() . Therefore,
. Therefore,
a contradiction. Thus, $[u_n]_{s_1,p} \rightarrow [\tilde {u}]_{s_1,p}$![]() in ${\mathbb {R}}^+$
in ${\mathbb {R}}^+$![]() . Hence from the uniform convexity of ${W_0^{s_1,p}(\Omega )}$
. Hence from the uniform convexity of ${W_0^{s_1,p}(\Omega )}$![]() , $u_n \rightarrow \tilde {u}$
, $u_n \rightarrow \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Step 3: In this step we prove that $\tilde {u}$
. Step 3: In this step we prove that $\tilde {u}$![]() is a positive solution of (EV; α, β). Since $u_n \rightarrow \tilde {u}$
is a positive solution of (EV; α, β). Since $u_n \rightarrow \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() , we obtain $d = I_+(\tilde {u})$
, we obtain $d = I_+(\tilde {u})$![]() and $\big < I_+'(\tilde {u}),\, \tilde {u} \big >=0$
and $\big < I_+'(\tilde {u}),\, \tilde {u} \big >=0$![]() . Using the continuity of $H_{\alpha }$
. Using the continuity of $H_{\alpha }$![]() and $G_{\beta }$
and $G_{\beta }$![]() , $H_{\alpha }(\tilde {u}) \le 0 \le G_{\beta }(\tilde {u})$
, $H_{\alpha }(\tilde {u}) \le 0 \le G_{\beta }(\tilde {u})$![]() . Next, we show $\tilde {u}$
. Next, we show $\tilde {u}$![]() is nonzero. Set $w_n = u_n [u_n]_{s_1,p}^{-1}$
is nonzero. Set $w_n = u_n [u_n]_{s_1,p}^{-1}$![]() . Then $w_n \rightharpoonup w$
. Then $w_n \rightharpoonup w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Since $H_{\alpha }(u_n)<0$
. Since $H_{\alpha }(u_n)<0$![]() , from the same arguments as in previous steps, $w \neq 0$
, from the same arguments as in previous steps, $w \neq 0$![]() and $G_{\beta }(w)>0$
and $G_{\beta }(w)>0$![]() . Next, suppose $[u_n]_{s_1,p} \rightarrow 0$
. Next, suppose $[u_n]_{s_1,p} \rightarrow 0$![]() as $n \rightarrow \infty$
as $n \rightarrow \infty$![]() . Using $G_{\beta }(w_n) \ge 0$
. Using $G_{\beta }(w_n) \ge 0$![]() we get
we get
A contradiction, as $w \in L^p(\Omega )$![]() . Thus $\inf _{n \in \mathbb {N}} [u_n]_{s_1,p} >0$
. Thus $\inf _{n \in \mathbb {N}} [u_n]_{s_1,p} >0$![]() and $\alpha {\lVert }{\tilde {u}}{\rVert }_p^p \ge \lim _{n \rightarrow \infty } [u_n]_{s_1,p}^p >0$
and $\alpha {\lVert }{\tilde {u}}{\rVert }_p^p \ge \lim _{n \rightarrow \infty } [u_n]_{s_1,p}^p >0$![]() , which implies that $\tilde {u}$
, which implies that $\tilde {u}$![]() is nonzero in $\Omega$
is nonzero in $\Omega$![]() , and hence $\tilde {u} \in {\mathcal {N}}_{\alpha, \beta }$
, and hence $\tilde {u} \in {\mathcal {N}}_{\alpha, \beta }$![]() . Moreover, from lemma 6.3, $H_{\alpha }(\tilde {u}) < 0 < G_{\beta }(\tilde {u})$
. Moreover, from lemma 6.3, $H_{\alpha }(\tilde {u}) < 0 < G_{\beta }(\tilde {u})$![]() . Now, using proposition 5.6 and remark 5.1, we conclude $\tilde {u}$
. Now, using proposition 5.6 and remark 5.1, we conclude $\tilde {u}$![]() is a nonnegative solution of (EV; α, β). Furthermore, by proposition 4.3, $\tilde {u}>0$
is a nonnegative solution of (EV; α, β). Furthermore, by proposition 4.3, $\tilde {u}>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
(ii) Our proof uses the method of contradiction. Let $u \in {W_0^{s_1,p}(\Omega )}$![]() and $u>0$
and $u>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . From (v) of proposition 2.1 and Lemma 2.4, $u_k^{q-p}\phi _{s_2,q}^{p-q+1},\, u_k^{1-p}\phi _{s_2,q}^p \in {W_0^{s_1,p}(\Omega )}$
. From (v) of proposition 2.1 and Lemma 2.4, $u_k^{q-p}\phi _{s_2,q}^{p-q+1},\, u_k^{1-p}\phi _{s_2,q}^p \in {W_0^{s_1,p}(\Omega )}$![]() . Applying the discrete Picone's inequality ((ii) of lemma 2.3),
. Applying the discrete Picone's inequality ((ii) of lemma 2.3),

The monotone convergence theorem yields $u^{q-p}\phi _{s_2,q}^p \in L^1(\Omega )$![]() and $\int _{\Omega } u_k^{q-p}\phi _{s_2,q}^p \rightarrow \int _{\Omega } u^{q-p}\phi _{s_2,q}^p$
and $\int _{\Omega } u_k^{q-p}\phi _{s_2,q}^p \rightarrow \int _{\Omega } u^{q-p}\phi _{s_2,q}^p$![]() , as $k \rightarrow \infty$
, as $k \rightarrow \infty$![]() . Next, we again use the Picone's inequality ((i) of lemma 2.3), to get
. Next, we again use the Picone's inequality ((i) of lemma 2.3), to get

If $u$![]() is a solution of (EV; α, β), then taking $u_k^{1-p}\phi _{s_2,q}^p$
is a solution of (EV; α, β), then taking $u_k^{1-p}\phi _{s_2,q}^p$![]() as a test function we write
as a test function we write

Further, applying the monotone convergence theorem
Therefore, from (6.9), (6.10), and (6.11), we conclude

The above inequality yields $\alpha \le \alpha ^*_{s_1,p}$![]() , which is a contradiction. Thus there does not exist any positive solution for $\alpha > \alpha ^*_{s_1,p}$
, which is a contradiction. Thus there does not exist any positive solution for $\alpha > \alpha ^*_{s_1,p}$![]() .
.
Remark 6.5 Let $\alpha = \alpha ^*_{s_1,p}$![]() and $\beta = \lambda _{s_2,q}^1$
and $\beta = \lambda _{s_2,q}^1$![]() . We assume that (LI) holds. Then observe that $I_+(u) = \frac {p-q}{pq} G_{\beta }(u) \ge 0$
. We assume that (LI) holds. Then observe that $I_+(u) = \frac {p-q}{pq} G_{\beta }(u) \ge 0$![]() for every $u \in {\mathcal {N}}_{\alpha,\beta }$
for every $u \in {\mathcal {N}}_{\alpha,\beta }$![]() , and $H_{\alpha }(\phi _{s_2,q})=G_{\beta }(\phi _{s_2,q})=0$
, and $H_{\alpha }(\phi _{s_2,q})=G_{\beta }(\phi _{s_2,q})=0$![]() . Therefore, for any $t \neq 0$
. Therefore, for any $t \neq 0$![]() , we get $t \phi _{s_2,q} \in {\mathcal {N}}_{\alpha, \beta }$
, we get $t \phi _{s_2,q} \in {\mathcal {N}}_{\alpha, \beta }$![]() and $d=I_+(t \phi _{s_2,q}) = 0$
and $d=I_+(t \phi _{s_2,q}) = 0$![]() . On the other hand, suppose $\phi _{s_2,q}$
. On the other hand, suppose $\phi _{s_2,q}$![]() is a solution of
is a solution of
Then $\phi _{s_2,q}$![]() has to change it's sign in $\Omega$
has to change it's sign in $\Omega$![]() (since $\alpha ^*_{s_1,p} > \lambda _{s_1,p}^1$
(since $\alpha ^*_{s_1,p} > \lambda _{s_1,p}^1$![]() ), a contradiction. Thus $\phi _{s_2,q}$
), a contradiction. Thus $\phi _{s_2,q}$![]() does not satisfy (6.12) and hence $\phi _{s_2,q}$
does not satisfy (6.12) and hence $\phi _{s_2,q}$![]() is not a solution of (EV; α, β). Thus, in this case, there does not exist any solution of (EV; α, β) which minimizes $d$
is not a solution of (EV; α, β). Thus, in this case, there does not exist any solution of (EV; α, β) which minimizes $d$![]() .
.
For $\alpha \ge \lambda _{s_1,p}^1$![]() and $\beta \ge \lambda _{s_2,q}^1$
and $\beta \ge \lambda _{s_2,q}^1$![]() , analogously as in [Reference Bobkov and Tanaka9] we consider the following quantity:
, analogously as in [Reference Bobkov and Tanaka9] we consider the following quantity:

Since $u \in {W_0^{s_1,p}(\Omega )} \subset {W_0^{s_2,q}(\Omega )}$![]() , the quantity $\beta ^{\star }(\alpha ) < \infty$
, the quantity $\beta ^{\star }(\alpha ) < \infty$![]() .
.
Proposition 6.6 Let $\alpha \ge \lambda _{s_1,p}^1$![]() and $\beta \ge \lambda _{s_2,q}^1$
and $\beta \ge \lambda _{s_2,q}^1$![]() . Assume that (LI) holds. Then $\beta ^{\star }(\alpha )$
. Assume that (LI) holds. Then $\beta ^{\star }(\alpha )$![]() is attained. Further, if $\alpha < \alpha ^*_{s_1,p}$
is attained. Further, if $\alpha < \alpha ^*_{s_1,p}$![]() , then $\beta ^{\star }(\alpha ) > \lambda _{s_2,q}^1$
, then $\beta ^{\star }(\alpha ) > \lambda _{s_2,q}^1$![]() .
.
Proof. Due to the homogeneity,

Let $(u_n)$![]() be a minimizing sequence for $\beta ^{\star }(\alpha )$
be a minimizing sequence for $\beta ^{\star }(\alpha )$![]() in $\mathcal {M}$
in $\mathcal {M}$![]() . Suppose $[u_n]_{s_1,p} \rightarrow \infty$
. Suppose $[u_n]_{s_1,p} \rightarrow \infty$![]() . Then $H_{\alpha }(u_n) \le 0$
. Then $H_{\alpha }(u_n) \le 0$![]() implies $\alpha ^{\frac {1}{p}} {\lVert }{u_n}{\rVert }_p \ge [u_n]_{s_1,p} \rightarrow \infty$
implies $\alpha ^{\frac {1}{p}} {\lVert }{u_n}{\rVert }_p \ge [u_n]_{s_1,p} \rightarrow \infty$![]() . Set $w_n=u_n {\lVert }{u_n}{\rVert }_p^{-1}$
. Set $w_n=u_n {\lVert }{u_n}{\rVert }_p^{-1}$![]() . Then $[w_n]_{s_1,p} = [u_n]_{s_1,p} {\lVert }{u_n}{\rVert }_p^{-1} \le \alpha ^{\frac {1}{p}}$
. Then $[w_n]_{s_1,p} = [u_n]_{s_1,p} {\lVert }{u_n}{\rVert }_p^{-1} \le \alpha ^{\frac {1}{p}}$![]() , and $w_n \rightharpoonup w$
, and $w_n \rightharpoonup w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Using ${\lVert }{u_n}{\rVert }_q=1$
. Using ${\lVert }{u_n}{\rVert }_q=1$![]() , we get ${\lVert }{w_n}{\rVert }_q \rightarrow 0$
, we get ${\lVert }{w_n}{\rVert }_q \rightarrow 0$![]() in ${\mathbb {R}}^+$
in ${\mathbb {R}}^+$![]() . On the other hand, ${\lVert }{w_n}{\rVert }_p=1$
. On the other hand, ${\lVert }{w_n}{\rVert }_p=1$![]() . Now the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^{\gamma }(\Omega ); \gamma \in [1,\,p]$
. Now the compact embeddings of ${W_0^{s_1,p}(\Omega )} \hookrightarrow L^{\gamma }(\Omega ); \gamma \in [1,\,p]$![]() yield:
yield:
Clearly, $(a)$![]() and $(b)$
and $(b)$![]() contradict each other. Therefore, the sequence $(u_n)$
contradict each other. Therefore, the sequence $(u_n)$![]() is bounded in ${W_0^{s_1,p}(\Omega )}$
is bounded in ${W_0^{s_1,p}(\Omega )}$![]() . By the reflexivity, $u_n \rightharpoonup \tilde {u}$
. By the reflexivity, $u_n \rightharpoonup \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Further, $\tilde {u} \in \mathcal {M}$
. Further, $\tilde {u} \in \mathcal {M}$![]() follows from the compact embedding of ${W_0^{s_1,p}(\Omega )}$
follows from the compact embedding of ${W_0^{s_1,p}(\Omega )}$![]() and weak lower semicontinuity of $H_{\alpha }$
and weak lower semicontinuity of $H_{\alpha }$![]() . Therefore,
. Therefore,
Thus $\beta ^{\star }(\alpha )$![]() is attained. Clearly, $\beta ^{\star }(\alpha ) \ge \lambda _{s_2,q}^1$
is attained. Clearly, $\beta ^{\star }(\alpha ) \ge \lambda _{s_2,q}^1$![]() . If $\beta ^{\star }(\alpha ) = \lambda _{s_2,q}^1$
. If $\beta ^{\star }(\alpha ) = \lambda _{s_2,q}^1$![]() , then by the simplicity of $\lambda _{s_2,q}^1$
, then by the simplicity of $\lambda _{s_2,q}^1$![]() ((iv) of proposition 2.1), $\tilde {u} =c\phi _{s_2,q}$
((iv) of proposition 2.1), $\tilde {u} =c\phi _{s_2,q}$![]() for some $c\in {\mathbb {R}}$
for some $c\in {\mathbb {R}}$![]() . Further, since $\alpha < \alpha ^*_{s_1,p}$
. Further, since $\alpha < \alpha ^*_{s_1,p}$![]() , we get $H_{\alpha }(\tilde {u})= CH_{\alpha }(\phi _{s_2,q})>0$
, we get $H_{\alpha }(\tilde {u})= CH_{\alpha }(\phi _{s_2,q})>0$![]() , a contradiction to $\tilde {u} \in \mathcal {M}$
, a contradiction to $\tilde {u} \in \mathcal {M}$![]() . Thus $\beta ^{\star }(\alpha ) > \lambda _{s_2,q}^1$
. Thus $\beta ^{\star }(\alpha ) > \lambda _{s_2,q}^1$![]() .
.
Now we prove the existence of a positive solution for (EV; α, β) when $\alpha,\, \beta$![]() are larger than $\lambda _{s_1,p}^1,\, \lambda _{s_2,q}^1$
are larger than $\lambda _{s_1,p}^1,\, \lambda _{s_2,q}^1$![]() respectively.
respectively.
Proposition 6.7 Let $\lambda _{s_1,p}^1 \le \alpha < \alpha ^*_{s_1,p}$![]() and $\lambda _{s_2,q}^1 < \beta < \beta ^{\star }(\alpha )$
and $\lambda _{s_2,q}^1 < \beta < \beta ^{\star }(\alpha )$![]() . Assume that (LI) holds. Then (EV; α, β) admits a positive solution.
. Assume that (LI) holds. Then (EV; α, β) admits a positive solution.
Proof. We adapt the arguments as given in [Reference Bobkov and Tanaka9, Theorem 2.5]. As before, we will show that $d := \min \{I_+(u): u \in {\mathcal {N}}_{\alpha, \beta }\}$![]() is attained. Since $\beta > \lambda _{s_2,q}^1$
is attained. Since $\beta > \lambda _{s_2,q}^1$![]() and $\alpha <\alpha ^*_{s_1,p}$
and $\alpha <\alpha ^*_{s_1,p}$![]() , we have $G_{\beta }(\phi _{s_2,q})<0< H_{\alpha }(\phi _{s_2,q})$
, we have $G_{\beta }(\phi _{s_2,q})<0< H_{\alpha }(\phi _{s_2,q})$![]() . Then by proposition 5.7, there exists a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$
. Then by proposition 5.7, there exists a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$![]() such that $0>I_+(t_{\alpha,\beta }\phi _{s_2,q})=\min _{t \in {\mathbb {R}}^+} I_+(t\phi _{s_2,q})$
such that $0>I_+(t_{\alpha,\beta }\phi _{s_2,q})=\min _{t \in {\mathbb {R}}^+} I_+(t\phi _{s_2,q})$![]() . We also have $t_{\alpha,\beta }\phi _{s_2,q} \in {\mathcal {N}}_{\alpha,\beta }$
. We also have $t_{\alpha,\beta }\phi _{s_2,q} \in {\mathcal {N}}_{\alpha,\beta }$![]() . Therefore, $d<0$
. Therefore, $d<0$![]() . Let $(u_n)$
. Let $(u_n)$![]() be the minimizing sequence in ${\mathcal {N}}_{\alpha,\beta }$
be the minimizing sequence in ${\mathcal {N}}_{\alpha,\beta }$![]() for $d$
for $d$![]() . Then there exists $n_0 \in \mathbb {N}$
. Then there exists $n_0 \in \mathbb {N}$![]() such that $I_+(u_n)<0$
such that $I_+(u_n)<0$![]() for $n \ge n_0$
for $n \ge n_0$![]() . Since $u_n \in {\mathcal {N}}_{\alpha,\beta }$
. Since $u_n \in {\mathcal {N}}_{\alpha,\beta }$![]() , using (i) of remark 5.8, $G_{\beta }(u_n)< 0 < H_{\alpha }(u_n)$
, using (i) of remark 5.8, $G_{\beta }(u_n)< 0 < H_{\alpha }(u_n)$![]() for $n \ge n_0$
for $n \ge n_0$![]() . Step 1: In this step, we show that $(u_n)$
. Step 1: In this step, we show that $(u_n)$![]() is a bounded sequence in ${W_0^{s_1,p}(\Omega )}$
is a bounded sequence in ${W_0^{s_1,p}(\Omega )}$![]() . As before, to prove this we argue by contradiction. Suppose $[u_n]_{s_1,p} \rightarrow \infty$
. As before, to prove this we argue by contradiction. Suppose $[u_n]_{s_1,p} \rightarrow \infty$![]() , as $n \rightarrow \infty$
, as $n \rightarrow \infty$![]() , and set $w_n = u_n [u_n]_{s_1,p}^{-1}$
, and set $w_n = u_n [u_n]_{s_1,p}^{-1}$![]() . Then $w_n \rightharpoonup w$
. Then $w_n \rightharpoonup w$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Hence
. Hence
which implies that $w \neq 0$![]() . Therefore, from the definition, $\beta ^{\star }(\alpha ) \le [w]_{s_2,q}^q {\lVert }{w}{\rVert }_q^{-q}$
. Therefore, from the definition, $\beta ^{\star }(\alpha ) \le [w]_{s_2,q}^q {\lVert }{w}{\rVert }_q^{-q}$![]() . Using this inequality along with $\beta < \beta ^{\star }(\alpha )$
. Using this inequality along with $\beta < \beta ^{\star }(\alpha )$![]() , we get $G_{\beta }(w) >0$
, we get $G_{\beta }(w) >0$![]() . On the other hand, $G_{\beta }(w) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } G_{\beta }(w_n) \le 0$
. On the other hand, $G_{\beta }(w) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } G_{\beta }(w_n) \le 0$![]() , a contradiction. Step 2: Let $u_n \rightharpoonup \tilde {u}$
, a contradiction. Step 2: Let $u_n \rightharpoonup \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . This step shows that $\tilde {u}$
. This step shows that $\tilde {u}$![]() is a positive solution of (EV; α, β). First, we claim ${H_{\alpha }(\tilde {u})>0}$
is a positive solution of (EV; α, β). First, we claim ${H_{\alpha }(\tilde {u})>0}$![]() . On a contrary, assume $H_{\alpha }(\tilde {u}) \le 0$
. On a contrary, assume $H_{\alpha }(\tilde {u}) \le 0$![]() . Since $I_+(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } I_+(u_n) \le d <0$
. Since $I_+(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } I_+(u_n) \le d <0$![]() , we get $\tilde {u}\neq 0.$
, we get $\tilde {u}\neq 0.$![]() Hence $\beta ^{\star }(\alpha ) \le [\tilde {u}]_{s_2,q}^q {\lVert }{\tilde {u}}{\rVert }_q^{-q}$
Hence $\beta ^{\star }(\alpha ) \le [\tilde {u}]_{s_2,q}^q {\lVert }{\tilde {u}}{\rVert }_q^{-q}$![]() and $\beta < \beta ^{\star }(\alpha )$
and $\beta < \beta ^{\star }(\alpha )$![]() imply $G_{\beta }(\tilde {u}) > 0$
imply $G_{\beta }(\tilde {u}) > 0$![]() . On the other hand, $G_{\beta }(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } G_{\beta }(u_n) \le 0$
. On the other hand, $G_{\beta }(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } G_{\beta }(u_n) \le 0$![]() , a contradiction. Therefore, $H_{\alpha }(\tilde {u})>0$
, a contradiction. Therefore, $H_{\alpha }(\tilde {u})>0$![]() . Further, $H_{\alpha }(\tilde {u})+ G_{\beta }(\tilde {u}) = I_+(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } I_+(u_n) \le 0$
. Further, $H_{\alpha }(\tilde {u})+ G_{\beta }(\tilde {u}) = I_+(\tilde {u}) \le \mathop {\operatorname {\underline {lim}}}_{n \rightarrow \infty } I_+(u_n) \le 0$![]() yields $G_{\beta }(\tilde {u})<0$
yields $G_{\beta }(\tilde {u})<0$![]() . Now we can use proposition 5.7, to get a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$
. Now we can use proposition 5.7, to get a unique $t_{\alpha,\beta } \in {\mathbb {R}}^+$![]() that minimizes $I_+(t \tilde {u})$
that minimizes $I_+(t \tilde {u})$![]() over ${\mathbb {R}}^+$
over ${\mathbb {R}}^+$![]() , and $t_{\alpha,\beta } \tilde {u} \in {\mathcal {N}}_{\alpha,\beta }$
, and $t_{\alpha,\beta } \tilde {u} \in {\mathcal {N}}_{\alpha,\beta }$![]() . Hence
. Hence
Thus, $I_+(t_{\alpha,\beta } \tilde {u})=I_+(\tilde {u})=d$![]() and from the uniqueness of $t_{\alpha, \beta }$
and from the uniqueness of $t_{\alpha, \beta }$![]() , we get $\tilde {u} \in {\mathcal {N}}_{\alpha,\beta }$
, we get $\tilde {u} \in {\mathcal {N}}_{\alpha,\beta }$![]() . Therefore, by proposition 5.6 and remark 5.1, $\tilde {u}$
. Therefore, by proposition 5.6 and remark 5.1, $\tilde {u}$![]() is a nonnegative solution of (EV; α, β). Further, using proposition 4.3, $\tilde {u}>0$
is a nonnegative solution of (EV; α, β). Further, using proposition 4.3, $\tilde {u}>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
Remark 6.8 Suppose (LI) holds. We consider

Then for each $\epsilon \in (0,\, \epsilon _1)$![]() , using proposition 6.7 we can conclude that (EV; $\lambda _{s_1,p}^1+ \epsilon,\,\lambda _{s_2,q}^1 + \epsilon$
, using proposition 6.7 we can conclude that (EV; $\lambda _{s_1,p}^1+ \epsilon,\,\lambda _{s_2,q}^1 + \epsilon$![]() ) admits a positive solution.
) admits a positive solution.
Recall that, $\lambda ^*(\theta )$![]() (where $\theta \in \mathbb {R}$
(where $\theta \in \mathbb {R}$![]() ) is defined as
) is defined as
Next, we prove some properties of the curve $\mathcal {C}:= \{(\lambda ^*(\theta ) + \theta,\, \lambda ^*(\theta )): \theta \in {\mathbb {R}}\}$![]() .
.
Proof of proposition 1.5. Proofs of (iii), (iv), and (vi) directly follow from [Reference Bobkov and Tanaka8, Proposition 3] with needful changes. So, we prove the remaining parts of the proposition. (i) Suppose $u\in {W_0^{s_1,p}(\Omega )}$![]() is a positive solution of (EV; $\lambda +\theta,\,\lambda$
is a positive solution of (EV; $\lambda +\theta,\,\lambda$![]() ) for some $\lambda \in \mathbb {R}.$
) for some $\lambda \in \mathbb {R}.$![]() For $v\in C_c^\infty(\Omega )$
For $v\in C_c^\infty(\Omega )$![]() with $v\geq 0$
with $v\geq 0$![]() , and for $k\in \mathbb {N}$
, and for $k\in \mathbb {N}$![]() , define $\phi _{k}:= \frac {v^p}{u_{k}^{p-1}+u_{k}^{q-1}}$
, define $\phi _{k}:= \frac {v^p}{u_{k}^{p-1}+u_{k}^{q-1}}$![]() . By lemma 2.4, $\phi _{k}\in {W_0^{s_1,p}(\Omega )}.$
. By lemma 2.4, $\phi _{k}\in {W_0^{s_1,p}(\Omega )}.$![]() Using the discrete Picone's inequalities ((iii) and (iv) of lemma 2.3), we obtain
Using the discrete Picone's inequalities ((iii) and (iv) of lemma 2.3), we obtain

Summing the above inequalities and by weak formulation of $u$![]() (where we use $\phi _{k}$
(where we use $\phi _{k}$![]() as a test function)
as a test function)

Further, using the monotone convergence theorem
This implies that
Since $v\in C_c^\infty(\Omega )$![]() , the R.H.S. of (6.13) is a positive constant independent of $\lambda$
, the R.H.S. of (6.13) is a positive constant independent of $\lambda$![]() and $u$
and $u$![]() . Hence, from (6.13) we conclude that $\lambda ^*(\theta )<\infty.$
. Hence, from (6.13) we conclude that $\lambda ^*(\theta )<\infty.$![]()
(ii) Sufficient condition: Suppose the property (LI) holds. By remark 6.8, we see that (EV; $\lambda ^1_{s_1,p}+\epsilon,\,\lambda ^1_{s_2,q}+\epsilon$![]() ) admits a positive solution for $\epsilon >0$
) admits a positive solution for $\epsilon >0$![]() small enough. From the definition of $\theta ^*$
small enough. From the definition of $\theta ^*$![]() , we have $(\lambda ^1_{s_1,p}+\epsilon,\,\lambda ^1_{s_2,q}+\epsilon )=(\lambda ^1_{s_2,q}+\epsilon +\theta ^*,\,\lambda ^1_{s_2,q}+\epsilon )$
, we have $(\lambda ^1_{s_1,p}+\epsilon,\,\lambda ^1_{s_2,q}+\epsilon )=(\lambda ^1_{s_2,q}+\epsilon +\theta ^*,\,\lambda ^1_{s_2,q}+\epsilon )$![]() . Hence from the definition of $\lambda ^*(\theta ^*)$
. Hence from the definition of $\lambda ^*(\theta ^*)$![]() , $\lambda ^*(\theta ^*)\geq \lambda ^1_{s_2,q}+\epsilon$
, $\lambda ^*(\theta ^*)\geq \lambda ^1_{s_2,q}+\epsilon$![]() , and $\lambda ^*(\theta ^*)+\theta ^*\geq \lambda ^1_{s_1,p}+\epsilon$
, and $\lambda ^*(\theta ^*)+\theta ^*\geq \lambda ^1_{s_1,p}+\epsilon$![]() .
.
Necessary condition: On a contrary assume that (LI) violates. This gives $\phi _{s_1,p}$![]() is an eigenfunction of $(-\Delta )^{s_2}_q$
is an eigenfunction of $(-\Delta )^{s_2}_q$![]() . Let $u$
. Let $u$![]() be a positive solution of (EV; α, β) for some $\alpha,\,\beta \in \mathbb {R}.$
be a positive solution of (EV; α, β) for some $\alpha,\,\beta \in \mathbb {R}.$![]() For $k\in \mathbb {N}$
For $k\in \mathbb {N}$![]() , set
, set

From lemma 2.4, $v_k,\, w_k \in {W_0^{s_1,p}(\Omega )}$![]() . Using the discrete Picone's inequalities ((i) and (ii) of lemma 2.3) and proposition 2.1, we obtain
. Using the discrete Picone's inequalities ((i) and (ii) of lemma 2.3) and proposition 2.1, we obtain

and

where the last equality holds since $(\phi _{s_1,p},\, \lambda ^{1}_{s_2,q})$![]() is an eigenpair. Summing (6.14), (6.15) and using $u$
is an eigenpair. Summing (6.14), (6.15) and using $u$![]() is a solution of (EV; α, β) with the test function $v_k$
is a solution of (EV; α, β) with the test function $v_k$![]() we obtain
we obtain

Therefore, by the monotone convergence theorem
a contradiction if $\alpha >\lambda ^{1}_{s_1,p}$![]() and $\beta >\lambda ^{1}_{s_2,q}$
and $\beta >\lambda ^{1}_{s_2,q}$![]() hold simultaneously. Thus if (LI) is violated, then there does not exist any $\beta > \lambda _{s_2,q}^1$
hold simultaneously. Thus if (LI) is violated, then there does not exist any $\beta > \lambda _{s_2,q}^1$![]() so that (EV; $\beta +\theta ^*,\,\beta$
so that (EV; $\beta +\theta ^*,\,\beta$![]() ) admits a positive solution.
) admits a positive solution.
(v) The proof consists of the following two cases.
Case 1: If (LI) does not hold, then $\theta ^*=\theta ^*_+$![]() and also, $\lambda ^*(\theta ^*)\leq \lambda ^1_{s_2,q}$
and also, $\lambda ^*(\theta ^*)\leq \lambda ^1_{s_2,q}$![]() (by (ii)). Hence using the decreasing property (iv) of $\lambda ^*(\theta )$
(by (ii)). Hence using the decreasing property (iv) of $\lambda ^*(\theta )$![]() , we get $\lambda ^*(\theta )\leq \lambda ^1_{s_2,q}$
, we get $\lambda ^*(\theta )\leq \lambda ^1_{s_2,q}$![]() for all $\theta \geq \theta ^*_+.$
for all $\theta \geq \theta ^*_+.$![]() Therefore, the result follows in this case by using (iii).
Therefore, the result follows in this case by using (iii).
Case 2: Let (LI) holds. We argue by contradiction. Suppose, there exists $\theta _0\geq \theta ^*_+$![]() such that $\lambda ^*(\theta _0)>\lambda ^1_{s_2,q}$
such that $\lambda ^*(\theta _0)>\lambda ^1_{s_2,q}$![]() . By increasing property (iv) together with (ii), we get $\lambda ^*(\theta _0)+\theta _0\geq \lambda ^*(\theta ^*)+\theta ^*>\lambda ^1_{s_1,p}$
. By increasing property (iv) together with (ii), we get $\lambda ^*(\theta _0)+\theta _0\geq \lambda ^*(\theta ^*)+\theta ^*>\lambda ^1_{s_1,p}$![]() . By the definition of $\lambda ^*(\theta _0)$
. By the definition of $\lambda ^*(\theta _0)$![]() , for any $\delta _0>0$
, for any $\delta _0>0$![]() there exists $\delta \in [0,\,\delta _0)$
there exists $\delta \in [0,\,\delta _0)$![]() such that (EV; $\lambda ^*(\theta _0)+\theta _0-\delta,\,\lambda ^*(\theta _0)-\delta$
such that (EV; $\lambda ^*(\theta _0)+\theta _0-\delta,\,\lambda ^*(\theta _0)-\delta$![]() ) admits a positive solution and we let $u$
) admits a positive solution and we let $u$![]() be such solution. We choose $\delta _0>0$
be such solution. We choose $\delta _0>0$![]() sufficiently small such that the following hold:
sufficiently small such that the following hold:
Now, by the weak formulation of $u$![]() and using discrete Picone's inequalities as in (6.14) and (6.15) (where we replace $\phi _{s_2,q}$
and using discrete Picone's inequalities as in (6.14) and (6.15) (where we replace $\phi _{s_2,q}$![]() by $\phi _{s_1,p}$
by $\phi _{s_1,p}$![]() in the test function $v_k$
in the test function $v_k$![]() )
)

Letting $k \rightarrow \infty$![]() and applying the monotone convergence theorem in the above, we obtain
and applying the monotone convergence theorem in the above, we obtain

Again, since $\delta <\delta _0$![]() , we obtain from (6.16) that
, we obtain from (6.16) that


and this implies $\theta _0<\frac {[\phi _{s_2,q}]^p_{s_1,p}}{{\lVert }{\phi _{s_2,q}}{\rVert }^p_p}-\lambda ^1_{s_2,q}=\theta ^*_+,$![]() a contradiction to $\theta _0\geq \theta ^*_+.$
a contradiction to $\theta _0\geq \theta ^*_+.$![]() This completes the proof.
This completes the proof.
Proof of theorem 1.6. (i) Suppose $\beta \in (\lambda _{s_2,q}^1,\, \lambda ^*(\theta ))$![]() . From the definition of $\lambda ^*$
. From the definition of $\lambda ^*$![]() , there exists $\mu \in (\beta,\, \lambda ^*(\theta ))$
, there exists $\mu \in (\beta,\, \lambda ^*(\theta ))$![]() such that (EV; $\mu +\theta,\,\mu$
such that (EV; $\mu +\theta,\,\mu$![]() ) has a positive solution $\overline {u} \in {W_0^{s_1,p}(\Omega )}$
) has a positive solution $\overline {u} \in {W_0^{s_1,p}(\Omega )}$![]() and from theorem 4.1, $\overline {u} \in L^{\infty }(\mathbb {R}^d)$
and from theorem 4.1, $\overline {u} \in L^{\infty }(\mathbb {R}^d)$![]() . Further, since $\mu > \beta$
. Further, since $\mu > \beta$![]() , $\overline {u}$
, $\overline {u}$![]() is a supersolution for (EV; $\beta +\theta,\,\beta$
is a supersolution for (EV; $\beta +\theta,\,\beta$![]() ). Moreover, $0$
). Moreover, $0$![]() is a subsolution for (EV; $\beta +\theta,\,\beta$
is a subsolution for (EV; $\beta +\theta,\,\beta$![]() ). Therefore, using proposition 5.11, $\tilde {I}$
). Therefore, using proposition 5.11, $\tilde {I}$![]() admits a global minimizer $\tilde {u}$
admits a global minimizer $\tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() , and then using proposition 5.12 we infer that $\tilde {u} \in L^{\infty }(\mathbb {R}^d)$
, and then using proposition 5.12 we infer that $\tilde {u} \in L^{\infty }(\mathbb {R}^d)$![]() is a solution of (EV; α, β), satisfying $0 \le \tilde {u}(x) \le \overline {u}(x)$
is a solution of (EV; α, β), satisfying $0 \le \tilde {u}(x) \le \overline {u}(x)$![]() a.e. in $\mathbb {R}^d$
a.e. in $\mathbb {R}^d$![]() . Next, we show that $\tilde {u}$
. Next, we show that $\tilde {u}$![]() is nonzero. Choose $t>0$
is nonzero. Choose $t>0$![]() so that $t\phi _{s_2,q}<\overline {u}$
so that $t\phi _{s_2,q}<\overline {u}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Also $t\phi _{s_2,q} \ge 0$
. Also $t\phi _{s_2,q} \ge 0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . From (5.10), we then get $\tilde {I}(t\phi _{s_2,q})= \frac {t^p}{p} G_{\alpha }(\phi _{s_2,q}) + \frac {t^q}{q} G_{\beta }(\phi _{s_2,q}),$
. From (5.10), we then get $\tilde {I}(t\phi _{s_2,q})= \frac {t^p}{p} G_{\alpha }(\phi _{s_2,q}) + \frac {t^q}{q} G_{\beta }(\phi _{s_2,q}),$![]() where $G_{\beta }(\phi _{s_2,q})<0$
where $G_{\beta }(\phi _{s_2,q})<0$![]() since $\beta >\lambda _{s_2,q}^1$
since $\beta >\lambda _{s_2,q}^1$![]() . Moreover, using $q< p$
. Moreover, using $q< p$![]() , we can choose $t$
, we can choose $t$![]() sufficiently small such that $\tilde {I}(t\phi _{s_2,q})<0$
sufficiently small such that $\tilde {I}(t\phi _{s_2,q})<0$![]() . Therefore, since $\tilde {u}$
. Therefore, since $\tilde {u}$![]() is the global minimizer for $\tilde {I}$
is the global minimizer for $\tilde {I}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() , we must have $\tilde {I}(\tilde {u})<0$
, we must have $\tilde {I}(\tilde {u})<0$![]() , and hence $\tilde {u} \neq 0$
, and hence $\tilde {u} \neq 0$![]() in $\Omega$
in $\Omega$![]() . Now, applying the strong maximum principle (proposition 4.3), $\tilde {u}>0$
. Now, applying the strong maximum principle (proposition 4.3), $\tilde {u}>0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
(ii) If $\beta > \lambda _{s_2,q}^1$![]() , then using the previous arguments existence result holds. Now we assume $\beta = \lambda _{s_2,q}^1$
, then using the previous arguments existence result holds. Now we assume $\beta = \lambda _{s_2,q}^1$![]() . Since $\lambda _{s_2,q}^1 < \lambda ^*(\alpha -\beta )$
. Since $\lambda _{s_2,q}^1 < \lambda ^*(\alpha -\beta )$![]() and $\lambda ^*(\theta )$
and $\lambda ^*(\theta )$![]() (where $\theta = \alpha -\beta$
(where $\theta = \alpha -\beta$![]() ) is decreasing ((iv) of proposition 1.5), we have $\theta < \theta ^*_+$
) is decreasing ((iv) of proposition 1.5), we have $\theta < \theta ^*_+$![]() (from (v) of proposition 1.5). From the definition of $\theta ^*_+$
(from (v) of proposition 1.5). From the definition of $\theta ^*_+$![]() , it is easy to observe that $\theta < \theta ^*_+$
, it is easy to observe that $\theta < \theta ^*_+$![]() is equivalent to $\alpha < \alpha ^*_{s_1,p}$
is equivalent to $\alpha < \alpha ^*_{s_1,p}$![]() . Therefore, for $\beta = \lambda _{s_2,q}^1$
. Therefore, for $\beta = \lambda _{s_2,q}^1$![]() and $\alpha \in (\lambda _{s_1,p}^1,\, \alpha ^*_{s_1,p})$
and $\alpha \in (\lambda _{s_1,p}^1,\, \alpha ^*_{s_1,p})$![]() using proposition 6.4 we conclude that (EV; α, β) admits a positive solution.
using proposition 6.4 we conclude that (EV; α, β) admits a positive solution.
(iii) If $\beta > \lambda ^*(\alpha -\beta )$![]() , then from the definition of $\lambda ^*$
, then from the definition of $\lambda ^*$![]() we see that (EV; α, β) does not admit any positive solution.
we see that (EV; α, β) does not admit any positive solution.
Proof of theorem 1.7. (i) Let $\theta < \theta ^*_+$![]() . From proposition 1.5, $\beta := \lambda ^*(\theta ) > \lambda _{s_2,q}^1$
. From proposition 1.5, $\beta := \lambda ^*(\theta ) > \lambda _{s_2,q}^1$![]() , and $\alpha := \lambda ^*(\theta )+\theta > \lambda _{s_1,p}^1$
, and $\alpha := \lambda ^*(\theta )+\theta > \lambda _{s_1,p}^1$![]() . From the definition of $\lambda ^*$
. From the definition of $\lambda ^*$![]() , there exists a sequence $(\beta _n) \subset (\lambda _{s_2,q}^1,\, \lambda ^*(\theta ))$
, there exists a sequence $(\beta _n) \subset (\lambda _{s_2,q}^1,\, \lambda ^*(\theta ))$![]() , such that $\beta _n \rightarrow \beta$
, such that $\beta _n \rightarrow \beta$![]() and (EV; $\beta _n+\theta,\,\beta _n$
and (EV; $\beta _n+\theta,\,\beta _n$![]() ) admit a sequence of positive solutions $(u_n)$
) admit a sequence of positive solutions $(u_n)$![]() (by (i) of theorem 1.6). Now, using the similar set of arguments as given in proposition 5.3, we get $u_n \rightarrow \tilde {u}$
(by (i) of theorem 1.6). Now, using the similar set of arguments as given in proposition 5.3, we get $u_n \rightarrow \tilde {u}$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() . Thus, from the continuity of $I'$
. Thus, from the continuity of $I'$![]() , $\tilde {u}$
, $\tilde {u}$![]() is a nonnegative solution of (EV; α, β). Next, we show $\tilde {u} \neq 0$
is a nonnegative solution of (EV; α, β). Next, we show $\tilde {u} \neq 0$![]() . On a contrary, assume that $\tilde {u}=0$
. On a contrary, assume that $\tilde {u}=0$![]() . For each $n,\, k \in \mathbb {N}$
. For each $n,\, k \in \mathbb {N}$![]() , set $u_{n,k}(x)=u_n(x) + \frac {1}{k}$
, set $u_{n,k}(x)=u_n(x) + \frac {1}{k}$![]() . From lemma 2.4, $u_{n,k}^{1-q}\phi _{s_2,q}^{q} \in {W_0^{s_1,p}(\Omega )}$
. From lemma 2.4, $u_{n,k}^{1-q}\phi _{s_2,q}^{q} \in {W_0^{s_1,p}(\Omega )}$![]() . Therefore, since $u_n$
. Therefore, since $u_n$![]() is a solution of (EV; α, β)
is a solution of (EV; α, β)

Using the monotone convergence theorem, $\int _{\Omega } u_n^{p-1} \phi _{s_2,q}^q u_{n,k}^{1-q} \rightarrow \int _{\Omega } u_n^{p-q} \phi _{s_2,q}^q$![]() and $\int _{\Omega } u_n^{q-1} \phi _{s_2,q}^q u_{n,k}^{1-q} \rightarrow \int _{\Omega } \phi _{s_2,q}^q$
and $\int _{\Omega } u_n^{q-1} \phi _{s_2,q}^q u_{n,k}^{1-q} \rightarrow \int _{\Omega } \phi _{s_2,q}^q$![]() as $k \rightarrow \infty$
as $k \rightarrow \infty$![]() . Next, from (i) of lemma 2.3 and using $u_{n,k}(x) - u_{n,k}(y) = u_n(x) - u_n(y)$
. Next, from (i) of lemma 2.3 and using $u_{n,k}(x) - u_{n,k}(y) = u_n(x) - u_n(y)$![]() , we get
, we get

Further, by the Hölder inequality with the conjugate exponent $(\frac {p}{p-q},\, \frac {p}{q})$![]() we estimate the following inequalities:
we estimate the following inequalities:

Therefore, since $u_n \rightarrow 0$![]() in ${W_0^{s_1,p}(\Omega )}$
in ${W_0^{s_1,p}(\Omega )}$![]() , from (6.19) and (6.20) we obtain
, from (6.19) and (6.20) we obtain

The above inequality yields $\beta \le \lambda _{s_2,q}^1$![]() , a contradiction to $\beta > \lambda _{s_2,q}^1$
, a contradiction to $\beta > \lambda _{s_2,q}^1$![]() . Therefore, $\tilde {u} \neq 0$
. Therefore, $\tilde {u} \neq 0$![]() and from the strong maximum principle (proposition 4.3), $\tilde {u} >0$
and from the strong maximum principle (proposition 4.3), $\tilde {u} >0$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
(ii) If $\theta > \theta ^*_+$![]() , then from (v) of proposition 1.5, the problem (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$
, then from (v) of proposition 1.5, the problem (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$![]() ) is equivalent to the problem (EV; α, β) where $\beta = \lambda _{s_2,q}^1$
) is equivalent to the problem (EV; α, β) where $\beta = \lambda _{s_2,q}^1$![]() and $\alpha = \lambda _{s_2,q}^1 + \theta > \lambda _{s_2,q}^1 + \theta ^*_+ > \alpha _{s_1,p}^*$
and $\alpha = \lambda _{s_2,q}^1 + \theta > \lambda _{s_2,q}^1 + \theta ^*_+ > \alpha _{s_1,p}^*$![]() . Therefore, by (ii) of proposition 6.4, (EV; α, β) does not admit any positive solution.
. Therefore, by (ii) of proposition 6.4, (EV; α, β) does not admit any positive solution.
Remark 6.9 Let $\theta = \theta ^*_+$![]() and (LI) holds. Then using (v) of proposition 1.5 and remark 6.5 we see that (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$
and (LI) holds. Then using (v) of proposition 1.5 and remark 6.5 we see that (EV; $\lambda ^*(\theta )+\theta,\,\lambda ^*(\theta )$![]() ) does not admit any solution which minimizes $d := \min \{I_+(u): u \in {\mathcal {N}}_{\alpha, \beta }\}$
) does not admit any solution which minimizes $d := \min \{I_+(u): u \in {\mathcal {N}}_{\alpha, \beta }\}$![]() .
.
Remark 6.10 In this remark, we represent $\lambda ^*(\theta )$![]() as a variational characterization. Let $\Omega \subset \mathbb {R}^d$
as a variational characterization. Let $\Omega \subset \mathbb {R}^d$![]() be a bounded open set with $C^{1,1}$
be a bounded open set with $C^{1,1}$![]() boundary $\partial \Omega$
boundary $\partial \Omega$![]() . We consider the following quantity:
. We consider the following quantity:

where $C(\overline {\Omega })_+ = \{u \in C(\overline {\Omega }) : u \ge 0\}$![]() and $\text {int}(C(\overline {\Omega })_+) = \{u \in C(\overline {\Omega })_+ : u > 0\}$
and $\text {int}(C(\overline {\Omega })_+) = \{u \in C(\overline {\Omega })_+ : u > 0\}$![]() . From theorem 1.6, we see that for certain ranges of $\lambda$
. From theorem 1.6, we see that for certain ranges of $\lambda$![]() , (EV; $\lambda +\theta,\,\lambda$
, (EV; $\lambda +\theta,\,\lambda$![]() ) admits a positive solution $u$
) admits a positive solution $u$![]() . Further, combining theorem 4.1 and [Reference Giacomoni, Kumar and Sreenadh24, Corollary 2.1], it is evident that the solution $u$
. Further, combining theorem 4.1 and [Reference Giacomoni, Kumar and Sreenadh24, Corollary 2.1], it is evident that the solution $u$![]() is in $C(\overline {\Omega })$
is in $C(\overline {\Omega })$![]() . Thus, $\text {int}(C(\overline {\Omega })_+)$
. Thus, $\text {int}(C(\overline {\Omega })_+)$![]() is nonempty and $\Lambda ^*(\theta )$
is nonempty and $\Lambda ^*(\theta )$![]() is well defined. Now, using the same arguments as given in [Reference Bobkov and Tanaka8, Proposition 5] we conclude that $\lambda ^*(\theta ) = \Lambda ^*(\theta )$
is well defined. Now, using the same arguments as given in [Reference Bobkov and Tanaka8, Proposition 5] we conclude that $\lambda ^*(\theta ) = \Lambda ^*(\theta )$![]() for every $\theta \in {\mathbb {R}}$
for every $\theta \in {\mathbb {R}}$![]() .
.
Acknowledgements
The authors thank Prof. Vladimir Bobkov for his valuable suggestions and comments, which improved the article. N. Biswas is supported by the Department of Atomic Energy, Government of India, under project no. 12-R $\& $![]() D-TFR-5.01-0520. F. Sk is supported by the Alexander von Humboldt foundation.
D-TFR-5.01-0520. F. Sk is supported by the Alexander von Humboldt foundation.