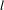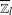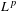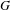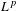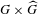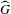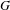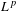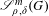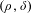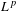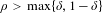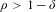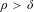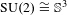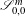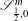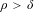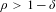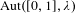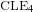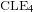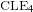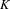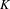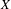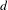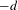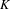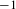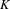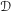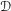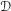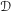Research Article
DUBROVIN’S SUPERPOTENTIAL AS A GLOBAL SPECTRAL CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2017, pp. 449-497
-
- Article
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
-
- Article
- Export citation
K-STABILITY OF FANO MANIFOLDS WITH NOT SMALL ALPHA INVARIANTS
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 519-530
-
- Article
- Export citation
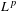 $L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
$L^{p}$-BOUNDS FOR PSEUDO-DIFFERENTIAL OPERATORS ON COMPACT LIE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 531-559
-
- Article
-
- You have access
- Open access
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2017, pp. 561-590
-
- Article
- Export citation
ON BOUNDED-TYPE THIN LOCAL SETS OF THE TWO-DIMENSIONAL GAUSSIAN FREE FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2017, pp. 591-618
-
- Article
- Export citation
VANISHING OF THE NEGATIVE HOMOTOPY
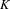 $K$-THEORY OF QUOTIENT SINGULARITIES
$K$-THEORY OF QUOTIENT SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 08 May 2017, pp. 619-627
-
- Article
- Export citation
RIEMANN–HILBERT CORRESPONDENCE FOR MIXED TWISTOR
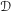 ${\mathcal{D}}$-MODULES
${\mathcal{D}}$-MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2017, pp. 629-672
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 18 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 18 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation