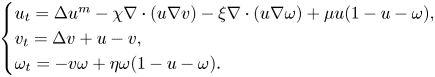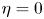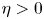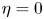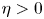1. Introduction
As a major disease threatening human life safety, cancer has always been the focus of social attention. The combination of mathematical models and various medical data will help people turn cancer research into a quantitative and predictable science. The mathematical modelling of tumour growth and its theoretical research have always been the concern of biologists and mathematicians. Generally speaking, the growth of a tumour usually goes through two stages: vascular phase and vascularization. That is, if there are no blood vessels to provide enough nutrients, the tumour will stop growing when it grows to a certain size. In order to continue to grow, some tumours will secrete a chemical substance, which is called urokinase Plasminogen Activator (uPA), to recruit vascular factors, and to build a vascular network around themselves to meet the growing nutritional needs. At the same time, blood vessels also provide a way for tumours to travel to other parts of the body, which is called metastasis. In recent years, some reaction-diffusion-taxis models are proposed to characterize the process of tumour growth and invasion [Reference Byrne, Chaplain, J.Pettet and Mcelwain1, Reference Chaplain and Anderson3, Reference Chaplain and Lolas4, Reference Stinner and Surulescu17]. In particular, the following model proposed by Chaplain and Lolas [Reference Chaplain and Lolas4] has attracted extensive attention of mathematicians in recent years.

which describes the invasion and diffusion process of solid tumours during the vascular growth stage. In this system, $u$![]() , $v$
, $v$![]() , $\omega$
, $\omega$![]() represent the cancer cell density, urokinase Plasminogen Activator (uPA) concentration, and the extracellular matrix (ECM) density respectively. $D(u)$
represent the cancer cell density, urokinase Plasminogen Activator (uPA) concentration, and the extracellular matrix (ECM) density respectively. $D(u)$![]() denotes the mobility of cells, the positive constants $\chi$
denotes the mobility of cells, the positive constants $\chi$![]() , $\xi$
, $\xi$![]() denote the uPA-mediated chemotaxis, ECM-mediated haptotaxis coefficients respectively, $\mu u(1-u-\omega )$
denote the uPA-mediated chemotaxis, ECM-mediated haptotaxis coefficients respectively, $\mu u(1-u-\omega )$![]() denotes the proliferation or death of cancer cells. In the second equation, $+u$
denotes the proliferation or death of cancer cells. In the second equation, $+u$![]() represents the production of uPA by cancer cells, $-v$
represents the production of uPA by cancer cells, $-v$![]() represents decay of uPA. As for the ECM density $\omega$
represents decay of uPA. As for the ECM density $\omega$![]() , it is known that it does not diffuse, therefore, one can omit the random motion. $-v\omega$
, it is known that it does not diffuse, therefore, one can omit the random motion. $-v\omega$![]() denotes the degradation of ECM, $\eta \omega (1-u-\omega )$
denotes the degradation of ECM, $\eta \omega (1-u-\omega )$![]() represents the remodelling of ECM components.
represents the remodelling of ECM components.
In the past ten years, this model has been widely studied. When $D(u)\equiv 1$![]() , $\eta =0$
, $\eta =0$![]() , we refer to [Reference Cao5, Reference Marciniak-Czochra and Ptashnyk13, Reference Tao and Wang18, Reference Walker and Webb23] for the study of global existence of bounded solutions, and refer to [Reference Hillen, Painter and Winkler6, Reference Tao and Winkler20, Reference Wang and Ke22] for the study of large time behaviour. While, if the remodelling of ECM is considered, the calculation of the haptotaxis term will bring some essential difficulties. Therefore, the following transformation is introduced to avoid the estimation of the haptotaxis term
, we refer to [Reference Cao5, Reference Marciniak-Czochra and Ptashnyk13, Reference Tao and Wang18, Reference Walker and Webb23] for the study of global existence of bounded solutions, and refer to [Reference Hillen, Painter and Winkler6, Reference Tao and Winkler20, Reference Wang and Ke22] for the study of large time behaviour. While, if the remodelling of ECM is considered, the calculation of the haptotaxis term will bring some essential difficulties. Therefore, the following transformation is introduced to avoid the estimation of the haptotaxis term
and the first equation of (1.1) is transformed into
Noticing that $\omega$![]() is bounded, then $\|u\|_{L^p}\sim \|\rho \|_{L^p}$
is bounded, then $\|u\|_{L^p}\sim \|\rho \|_{L^p}$![]() . Using this method, the global existence and boundedness of classical solution for any initial datum in two dimensional space is proved [Reference Jin10, Reference Pang and Wang15]. While in three dimensional space, only a small global classical solution is established [Reference Jin11, Reference Pang and Wang16]. In fact, even for the haptotaxis-only system, the global bounded solution for any $\mu,\, \eta >0$
. Using this method, the global existence and boundedness of classical solution for any initial datum in two dimensional space is proved [Reference Jin10, Reference Pang and Wang15]. While in three dimensional space, only a small global classical solution is established [Reference Jin11, Reference Pang and Wang16]. In fact, even for the haptotaxis-only system, the global bounded solution for any $\mu,\, \eta >0$![]() in dimension 3 is still open.
in dimension 3 is still open.
Considering the mechanism of avoiding crowding between individual cells, the mobility of cells should be related to density, so a model with nonlinear diffusion is also very practical, and the most representative one is the porous medium diffusion model. For example, in [Reference Byrne, Chaplain, J.Pettet and Mcelwain1, Reference Byrne, Chaplain, J.Pettet and Mcelwain2], the authors use porous medium diffusion to describe the process of trophoblast cells invading the uterine tissue, that is,

In 2011, Tao and Winkler [Reference Tao and Winkler19] first studied the global solvability of (1.1) by ignoring the remodelling of ECM, that is, for

they proved the global existence of weak solutions when

After that, the global existence of weak solutions to this problem began to be widely studied, see for example [Reference Jin7, Reference Li and Lankeit12, Reference Wang21, Reference Zheng24] etc. For this case, from the third equation of (1.4), one observed that
At this time, there are two commonly used methods to assist in dealing with the haptotactic term.
Method I: A direct calculation from (1.5) leads to
Therefore,

Similarly, one can use iteration to sequentially obtain $\|\nabla \omega (\cdot,\,t)\|_{L^4}$![]() , $\|\nabla \omega (\cdot,\,t)\|_{L^6}$
, $\|\nabla \omega (\cdot,\,t)\|_{L^6}$![]() , $\|\nabla \omega (\cdot,\,t)\|_{L^{2n}}\cdots$
, $\|\nabla \omega (\cdot,\,t)\|_{L^{2n}}\cdots$![]() .
.
Method II: A direct calculation from (1.5) leads to

where $K$![]() only depends on $\omega _0$
only depends on $\omega _0$![]() [Reference Tao and Winkler19]. Therefore, the above two methods can make the haptotactic term easy to handle, however, the two methods are obviously not suitable for situations where $\eta >0$
[Reference Tao and Winkler19]. Therefore, the above two methods can make the haptotactic term easy to handle, however, the two methods are obviously not suitable for situations where $\eta >0$![]() . In fact, if the remodelling of ECM is considered, that is, the third equation of (1.4) is replaced with
. In fact, if the remodelling of ECM is considered, that is, the third equation of (1.4) is replaced with
the problem becomes much more complex since the regularity of $\omega$![]() completely depends on the regularity of $u$
completely depends on the regularity of $u$![]() . Actually, due to that the ODE has no regularization effect, the regularity of $\omega$
. Actually, due to that the ODE has no regularization effect, the regularity of $\omega$![]() is greatly reduced by $-\eta u\omega$
is greatly reduced by $-\eta u\omega$![]() in remodelling term. Therefore, although a lot of results for the case $\eta =0$
in remodelling term. Therefore, although a lot of results for the case $\eta =0$![]() have been achieved in the past ten years, there is no any progress in the case of $\eta >0$
have been achieved in the past ten years, there is no any progress in the case of $\eta >0$![]() .
.
In the present paper, we consider the initial and boundary value problem for the system (1.1) with nonlinear diffusion, that is

where $Q=\Omega \times \mathbb {R}^+$![]() , $m>1$
, $m>1$![]() , $\Omega \subset \mathbb {R}^N$
, $\Omega \subset \mathbb {R}^N$![]() ($N\ge 2$
($N\ge 2$![]() ) is a smooth bounded domain. $\chi$
) is a smooth bounded domain. $\chi$![]() , $\xi$
, $\xi$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() are positive constants.
are positive constants.
According to previous research experience for some chemotaxis models, the larger $m$![]() is, the easier it is to prove the uniform boundedness of the solution, but this experience seems to be invalid for the current model. On the one hand, due to the existence of remodelling term $\eta \omega (1-u-\omega )$
is, the easier it is to prove the uniform boundedness of the solution, but this experience seems to be invalid for the current model. On the one hand, due to the existence of remodelling term $\eta \omega (1-u-\omega )$![]() , the methods (Method I and Method II) used in the study of equations (1.4) is completely invalid. On the other hand, due to the lack of a good coupling structure similar to the linear diffusion case between the diffusion term and the haptotactic term, the method used for the linear diffusion case (see (1.2)) is also not suitable for the current nonlinear diffusion model. Therefore, we have to try new methods. Fortunately, we found a complex relationship between the haptotactic term and the nonlinear diffusion term. In addition to constructing classical functional such as
, the methods (Method I and Method II) used in the study of equations (1.4) is completely invalid. On the other hand, due to the lack of a good coupling structure similar to the linear diffusion case between the diffusion term and the haptotactic term, the method used for the linear diffusion case (see (1.2)) is also not suitable for the current nonlinear diffusion model. Therefore, we have to try new methods. Fortunately, we found a complex relationship between the haptotactic term and the nonlinear diffusion term. In addition to constructing classical functional such as
we also construct the following new form of functionals

which allows us to reconstruct the relationship between nonlinear diffusion term and haptotactic term. In particular, by taking the derivative of the above functional, we can use the diffusion term to neutralize the ‘bad’ effect brought by the haptotactic term. That is (see lemma 3.6)

However, this also reduces the original good effect of the diffusion term. Fortunately, we have the logistic term, with the help of this term, we can finally get the $L^p$![]() -norm ($\forall$
-norm ($\forall$![]() $p>1$
$p>1$![]() )uniform estimation of $u$
)uniform estimation of $u$![]() and the $W^{1,\infty }$
and the $W^{1,\infty }$![]() -norm estimation of $v$
-norm estimation of $v$![]() . However, it is hard to get the $L^\infty$
. However, it is hard to get the $L^\infty$![]() -norm estimation of $u$
-norm estimation of $u$![]() since the Moser's iteration technique is no longer applicable due to the diffusion term is not working.
since the Moser's iteration technique is no longer applicable due to the diffusion term is not working.
Although the haptotactic term caused the main difficulties in the proof, we prove that the chemotaxis still plays a leading role in determining whether the solution can exist globally. More precisely, we prove that the weak solution will exists globally for any $m>\frac {2N}{N+2}$![]() if $\chi >0$
if $\chi >0$![]() , while for the haptotaxis-only model, that is the case $\chi =0$
, while for the haptotaxis-only model, that is the case $\chi =0$![]() . We prove that for any $m>1$
. We prove that for any $m>1$![]() , the solution always exists globally. This work obviously improves the results in references[Reference Li and Lankeit12, Reference Tao and Winkler19, Reference Wang21, Reference Zheng24], in which, only the special case $\eta =0$
, the solution always exists globally. This work obviously improves the results in references[Reference Li and Lankeit12, Reference Tao and Winkler19, Reference Wang21, Reference Zheng24], in which, only the special case $\eta =0$![]() is studied.
is studied.
In what follows, we give the assumptions of this paper.

We state the main results as follows.
Theorem 1.1 Assume that (H) holds, $\mu >0$![]() and $m>\frac {2N}{N+2}$
and $m>\frac {2N}{N+2}$![]() . Then the problem (1.6) admits a global nonnegative weak solution $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$
. Then the problem (1.6) admits a global nonnegative weak solution $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$![]() . In particular, $u,\, v,\, \omega$
. In particular, $u,\, v,\, \omega$![]() are bounded uniformly in the following sense
are bounded uniformly in the following sense
where $C_r$![]() only depends on $r$
only depends on $r$![]() , $\chi$
, $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() . Here
. Here

Although the haptotactic term caused the main difficulties in the proof, the requirement of this index $m>\frac {N+2}{2N}$![]() was still caused by the chemotactic term. In fact, if $\chi =0$
was still caused by the chemotactic term. In fact, if $\chi =0$![]() , we have the global existence result for any slow diffusion case $m>1$
, we have the global existence result for any slow diffusion case $m>1$![]() .
.
Theorem 1.2 Assume $\chi =0$![]() , $\mu >0$
, $\mu >0$![]() , $m>1$
, $m>1$![]() and (H) holds. Then the problem (1.6) admits a global nonnegative weak solution $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$
and (H) holds. Then the problem (1.6) admits a global nonnegative weak solution $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$![]() . In particular, $u,\, v,\, \omega$
. In particular, $u,\, v,\, \omega$![]() are bounded uniformly in the following sense
are bounded uniformly in the following sense
where $C_r$![]() only depends on $r$
only depends on $r$![]() , $\chi$
, $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
Remark 1.3 As for the stability of the equilibrium points, the local stability of equilibrium point $(1,\,1,\,0)$![]() is easy to obtain by linear stability analysis, see for example [Reference Jin11]. However, the research on global asymptotic stability of the equilibrium point is a very challenging problem. In fact, this problem is still unsolved even for linear diffusion case $m=1$
is easy to obtain by linear stability analysis, see for example [Reference Jin11]. However, the research on global asymptotic stability of the equilibrium point is a very challenging problem. In fact, this problem is still unsolved even for linear diffusion case $m=1$![]() .
.
2. Preliminaries
We first give the definition of weak solutions.
Definition 2.1 $(u,\, v,\, \omega )$![]() is called a nonnegative weak solution of (1.6), if $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_2$
is called a nonnegative weak solution of (1.6), if $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_2$![]() , such that for any $T>0$
, such that for any $T>0$![]() ,
,

for any $\varphi _1,\, \varphi _2,\, \varphi _3\in C^\infty (\overline Q_T)$![]() with $\varphi _i(x,\,T)=0$
with $\varphi _i(x,\,T)=0$![]() .
.
As a preparation, we introduce the following inequalities [Reference Jin8, Reference Jin9, Reference Mizoguchi and Souplet14], which is useful in the calculation of energy estimation.
Lemma 2.2 Assume that $\Omega$![]() is bounded with smooth boundary, and let $\omega \in C^2(\overline \Omega )$
is bounded with smooth boundary, and let $\omega \in C^2(\overline \Omega )$![]() satisfies $\frac {\partial \omega }{\partial \nu }\Big |_{\partial \Omega }=0$
satisfies $\frac {\partial \omega }{\partial \nu }\Big |_{\partial \Omega }=0$![]() . Then we have
. Then we have
where $\kappa >0$![]() is an upper bound for the curvatures of $\Omega$
is an upper bound for the curvatures of $\Omega$![]() . In particular, we have the following inequalities
. In particular, we have the following inequalities
and
where $\delta >0$![]() is an arbitrary small constant, and $C_\delta$
is an arbitrary small constant, and $C_\delta$![]() is a constant depending on $\delta$
is a constant depending on $\delta$![]() .
.
Using Neumann heat semigroup theory, we prove the following lemma.
Lemma 2.3 Let $\Omega \subset \mathbb {R}^N$![]() be a bounded domain with smooth boundary. Assume that $u\in L^q(\Omega \times (0,\, T))$
be a bounded domain with smooth boundary. Assume that $u\in L^q(\Omega \times (0,\, T))$![]() , $v_0\in W^{2,q}(\Omega )$
, $v_0\in W^{2,q}(\Omega )$![]() with $q\ge 2$
with $q\ge 2$![]() . Then the following problem admits
. Then the following problem admits

admits a unique strong solution ![]() $v\in W_q^{2,1}(\Omega \times (0,\, T))$, such that for any
$v\in W_q^{2,1}(\Omega \times (0,\, T))$, such that for any ![]() $r<\frac{Nq}{(N+2-q)_+}$,
$r<\frac{Nq}{(N+2-q)_+}$,

and

where $\tau =\min \left \{1,\, \frac {T}2\right \}$![]() , $C_i (i=1,\,2,\,3,\,4)$
, $C_i (i=1,\,2,\,3,\,4)$![]() are constants depending only on $v_0$
are constants depending only on $v_0$![]() , $\Omega$
, $\Omega$![]() .
.
Proof. By Duhamel's principle, $v$![]() can be expressed as follows
can be expressed as follows
where $\{e^{t\Delta }\}_{t\ge 0}$![]() is the Neumann heat semigroup in $\Omega$
is the Neumann heat semigroup in $\Omega$![]() . For any $r\in (1,\, +\infty )$
. For any $r\in (1,\, +\infty )$![]() , we have
, we have

A direct calculation gives
Then when $r<\frac {Nq}{(N+2-q)_+}$![]() ,
,

We also note that for any $t>0$![]() , there exists an integer $N$
, there exists an integer $N$![]() such that $t=N\tau +\sigma$
such that $t=N\tau +\sigma$![]() with $0<\sigma <\tau$
with $0<\sigma <\tau$![]() . Therefore, we have
. Therefore, we have

which implies that (2.5). By $L^p$![]() theory of linear parabolic equations, we obtain
theory of linear parabolic equations, we obtain
From Gagliardo-Nirenberg interpolation inequality, we infer that
3. Uniform energy estimations and global solvability of chemotaxis-haptotaxis system
In order to prove the existence of the weak solution of problem (1.6), some prior estimates are necessary. Since problem (1.6) is degenerate at $u = 0$![]() , in order to facilitate us to obtain various prior estimates later, we first use the standard method to build a framework, that is, consider its regularization problem
, in order to facilitate us to obtain various prior estimates later, we first use the standard method to build a framework, that is, consider its regularization problem

for any $\varepsilon \in (0,\,1)$![]() , and $(u_{\varepsilon 0},\, v_{\varepsilon 0},\, \omega _{\varepsilon 0})$
, and $(u_{\varepsilon 0},\, v_{\varepsilon 0},\, \omega _{\varepsilon 0})$![]() is smooth approximation of $(u_0,\, v_0,\, \omega _0)$
is smooth approximation of $(u_0,\, v_0,\, \omega _0)$![]() with $(u_{\varepsilon 0},\, v_{\varepsilon 0},\, \omega _{\varepsilon 0})$
with $(u_{\varepsilon 0},\, v_{\varepsilon 0},\, \omega _{\varepsilon 0})$![]() sufficiently smooth. By standard fixed point method, it is easy to obtain the local existence of classical solutions to the above problem, see for example [Reference Tao and Winkler19]. That is
sufficiently smooth. By standard fixed point method, it is easy to obtain the local existence of classical solutions to the above problem, see for example [Reference Tao and Winkler19]. That is
Lemma 3.1 Assume $B$![]() , $m>1$
, $m>1$![]() , $\varepsilon \in (0,\,1)$
, $\varepsilon \in (0,\,1)$![]() . Then there exists $T_{\max }\in (0,\, +\infty ]$
. Then there exists $T_{\max }\in (0,\, +\infty ]$![]() such that the problem (3.1) admits a classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q_{T_{\max }})\cap C^0(\overline \Omega \times [0,\,T_{\max }))$
such that the problem (3.1) admits a classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q_{T_{\max }})\cap C^0(\overline \Omega \times [0,\,T_{\max }))$![]() with
with
Moreover, we have the following dichotomy: Either $T_{\max } = \infty$![]() , or
, or
Throughout this paper, we denote
In what follows, we focus on the uniform energy estimates of $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$![]() . For simplicity, we omit the subscript $\varepsilon$
. For simplicity, we omit the subscript $\varepsilon$![]() of the approximate solutions $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$
of the approximate solutions $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$![]() in the subsequent energy estimate calculations.
in the subsequent energy estimate calculations.
Firstly, it is easy to obtain the following estimates.
Lemma 3.2 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Then
. Then
where the constants $C_1$![]() , $C_2$
, $C_2$![]() only depend on $\mu$
only depend on $\mu$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() and $\Omega$
and $\Omega$![]() .
.
Proof. By comparison lemma, it is easy to see that
By direct integration over $\Omega$![]() for the first equation of (3.1), (3.2) is easy to be obtained. By $L^2$
for the first equation of (3.1), (3.2) is easy to be obtained. By $L^2$![]() theory of linear parabolic equations, (3.3) is arrived.
theory of linear parabolic equations, (3.3) is arrived.
Lemma 3.3 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Then for any $T< T_{\max }$
. Then for any $T< T_{\max }$![]() ,
,

where $C_T$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() , it depends only on $\chi$
, it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() , and $T$
, and $T$![]() .
.
In particular, we also have

where $C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $\chi$
, it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
It should be noted that the estimation (3.4) is time-dependent, but (3.5) is not time-dependent. Although (3.5) depends on $\varepsilon$![]() , it is useful for us to obtain uniform estimations independent of time and $\varepsilon$
, it is useful for us to obtain uniform estimations independent of time and $\varepsilon$![]() .
.
Proof. By direct calculation,

Similar to the proof of lemma 2.6 in [Reference Jin8], we have
Putting the above two equalities together, we get the following conclusion

Multiplying both sides of the first equation of (3.1) by $1+\ln u$![]() , and integrating the resultant equation over $\Omega$
, and integrating the resultant equation over $\Omega$![]() yields
yields

The combination of (3.6) and (3.7) leads to

Recalling (2.4), we have
We substitute (3.9) into (3.8) to obtain

Using (3.2) and (3.3), by direct calculation, we complete the proof of (3.4).
On the other hand, we note that
which together with (3.10) yields

where $\tilde C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() . Denote
. Denote
clearly,

Then (3.12) implies that
Then the uniform boundedness of $f$![]() is derived from (3.2) and (3.3). Furthermore, (3.5) is obtained by integrating (3.12) from $t-\tau$
is derived from (3.2) and (3.3). Furthermore, (3.5) is obtained by integrating (3.12) from $t-\tau$![]() to $t$
to $t$![]() .
.
Next, our purpose is to continuously improve the regularity of the solution. In this process, the key is to deal with the haptotaxis term. We try to offset the influence of the haptotaxis term with the diffusion term. First, we can get the following lemma.
Lemma 3.4 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() , and assume $m>\frac {2N}{N+2}$
, and assume $m>\frac {2N}{N+2}$![]() . Then
. Then

where $C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , and it depends only on $\chi$
, and it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
In addition, we also have
and for any $1< p<2$![]() ,
,
where $C_T$![]() , $C_{Tp}$
, $C_{Tp}$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() , and $C_T$
, and $C_T$![]() depends on $T$
depends on $T$![]() , $C_{Tp}$
, $C_{Tp}$![]() depends on $T$
depends on $T$![]() and $p$
and $p$![]() .
.
Proof. Noticing that

that is
Recalling (2.2), we conclude

Noticing that

multiplying both sides of the first equation of (3.1) by $\frac {m}{m-1}(u+\varepsilon )^{m-1}-\xi \omega$![]() , and using (3.17), (3.5) and lemma 3.2, we arrive at
, and using (3.17), (3.5) and lemma 3.2, we arrive at

namely,

Taking advantage of Gagliardo-Nirenberg interpolation inequality and (3.3), we have

Noticing that $\frac {(N+2)(m+1)}{N}>\frac {2(m+1)}m$![]() when $m>\frac {2N}{N+2}$
when $m>\frac {2N}{N+2}$![]() , we infer from (3.18), (3.19),
, we infer from (3.18), (3.19),

for any small constant $\sigma >0$![]() , with $C_\sigma$
, with $C_\sigma$![]() depending on $\sigma$
depending on $\sigma$![]() . Noticing that
. Noticing that
and using $L^p$![]() theory of linear parabolic equations, we conclude that
theory of linear parabolic equations, we conclude that

Here, all these constants $C_i$![]() , $\hat C$
, $\hat C$![]() , $\tilde C$
, $\tilde C$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() . By the arbitrariness of $\sigma$
. By the arbitrariness of $\sigma$![]() , using (3.5), (3.16), and (3.13) is proved by taking $\sigma$
, using (3.5), (3.16), and (3.13) is proved by taking $\sigma$![]() appropriately small in the above inequality.
appropriately small in the above inequality.
In addition, using (3.3), (3.4) and (3.13), and noticing that

we arrive at (3.14).
For any $1< p<2$![]() , we also notice that
, we also notice that

Then (3.15) is derived from (3.14) and the above inequality.
To improve the regularity of $u$![]() , we need the following estimate on $\omega$
, we need the following estimate on $\omega$![]() . Although this estimation does not depend on $T_{\max }$
. Although this estimation does not depend on $T_{\max }$![]() , it depends on $\varepsilon$
, it depends on $\varepsilon$![]() . In order to obtain some subsequent uniform estimates that does not depend on $\varepsilon$
. In order to obtain some subsequent uniform estimates that does not depend on $\varepsilon$![]() , we need to the exact order of its dependence on $\varepsilon$
, we need to the exact order of its dependence on $\varepsilon$![]() .
.
Lemma 3.5 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Then for any $r>2$
. Then for any $r>2$![]() ,
,

where $\tilde C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $\chi$
, it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $r$
, $r$![]() , $\Omega$
, $\Omega$![]() .
.
Proof. Applying $\nabla$![]() to the third equation of (3.1), multiplying both sides of the resultant equation by $|\nabla \omega |^{r-2}\nabla \omega$
to the third equation of (3.1), multiplying both sides of the resultant equation by $|\nabla \omega |^{r-2}\nabla \omega$![]() for any $r>2$
for any $r>2$![]() , and using lemma 2.2, we obtain
, and using lemma 2.2, we obtain

Recalling (2.3), and noticing that $\omega$![]() is bounded, then there exists a constant $\rho$
is bounded, then there exists a constant $\rho$![]() such that
such that
By the boundary trace embedding inequalities, we conclude that for any small $\delta >0$![]() ,
,
The combination of (3.22)–(3.24) leads to

It implies that
Using (3.26), and integrating (3.25) directly, we arrive at
Here these constants $C_i$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() . Then (3.21) is derived from (3.26) and (3.27).
. Then (3.21) is derived from (3.26) and (3.27).
Based on the above lemmas, we can improve the regularity of the solution, and obtain the following result.
Lemma 3.6 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Assume that $m>\frac {2N}{N+2}$
. Assume that $m>\frac {2N}{N+2}$![]() . Then for any positive integer $k$
. Then for any positive integer $k$![]() , we have
, we have

where $C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $k$
, it depends only on $k$![]() , $\chi$
, $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
Proof. For any given positive integer $k$![]() , multiplying both sides of the first equation of (3.1) by $(\frac {m}{m-1}(u+\varepsilon )^{m-1}-\xi \omega )^{2k+1}$
, multiplying both sides of the first equation of (3.1) by $(\frac {m}{m-1}(u+\varepsilon )^{m-1}-\xi \omega )^{2k+1}$![]() , recalling (3.17), and noticing that $\omega$
, recalling (3.17), and noticing that $\omega$![]() is bounded, then we arrive at
is bounded, then we arrive at

That is

We first calculate the first term on the left of the above inequality.

In what follows, we calculate $I$![]() , $II$
, $II$![]() respectively. Using Young's inequality and recalling (3.5), it is not difficult to see that
respectively. Using Young's inequality and recalling (3.5), it is not difficult to see that

Noticing that $\omega$![]() is bounded, and using (3.3) gives
is bounded, and using (3.3) gives

Next, we estimate the second term $\displaystyle C_6\int _{\Omega }|\nabla v|^{\frac {4k(m-1)+2(m+1)}{m}} {\rm d}x$![]() in (3.32). From Gagliardo-Nirenberg inequality, we infer that
in (3.32). From Gagliardo-Nirenberg inequality, we infer that
By direct calculation, it is easy to obtain
When $N=2$![]() , take
, take
in (3.33). Then $p\alpha < q_1$![]() . Using (3.3), we infer from (3.33) that for any small constant $\rho >0$
. Using (3.3), we infer from (3.33) that for any small constant $\rho >0$![]() ,
,

since $p\alpha < q_1$![]() .
.
When $N\ge 3$![]() . By (2.5) and (3.13), we see that
. By (2.5) and (3.13), we see that
We take

in (3.33). Then $\|\nabla v\|_{L^{q_2}}$![]() is uniformly bounded by (3.35), and
is uniformly bounded by (3.35), and
By direct verification, the above inequality $\frac {2}m<1+\frac {m+\frac {5}{2N}}{(N+1-m)_+}$![]() holds when $m>\frac {2N}{N+2}$
holds when $m>\frac {2N}{N+2}$![]() . Then
. Then
for any small constant $\rho >0$![]() .
.
Substituting (3.34) and (3.36) into (3.32) yields

for any small constant $\rho >0$![]() with $\hat C_\rho$
with $\hat C_\rho$![]() depending on $\rho$
depending on $\rho$![]() .
.
By substituting the inequalities (3.30), (3.31) and (3.37) into (3.29) yields

Noticing that

and for any small constant $\rho >0$![]() , there exists a constant $C_\rho$
, there exists a constant $C_\rho$![]() such that
such that

combining (3.21), and using $L^p$![]() theory of linear parabolic equations, from (3.38) we derive
theory of linear parabolic equations, from (3.38) we derive

Take $\rho$![]() appropriately small in the above inequality, such that $C_{16}\rho <\frac {\mu }8(\frac {m}{m-1})^{2k+1}$
appropriately small in the above inequality, such that $C_{16}\rho <\frac {\mu }8(\frac {m}{m-1})^{2k+1}$![]() . Then we finally arrive that
. Then we finally arrive that

which implies (3.28).
By (3.28), there exists $k$![]() sufficiently large such that $(m-1)(2k+1)+1>N$
sufficiently large such that $(m-1)(2k+1)+1>N$![]() , then by Neumann heat semigroup theory, it is easy to obtain the $L^\infty$
, then by Neumann heat semigroup theory, it is easy to obtain the $L^\infty$![]() estimation of $\nabla v$
estimation of $\nabla v$![]() . By $L^p$
. By $L^p$![]() theory of linear parabolic equations, we also have $W_p^{2,1}$
theory of linear parabolic equations, we also have $W_p^{2,1}$![]() estimation of $v$
estimation of $v$![]() and $L^p$
and $L^p$![]() estimation of $\omega _t$
estimation of $\omega _t$![]() .
.
Lemma 3.7 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Assume that $m>\frac {2N}{N+2}$
. Assume that $m>\frac {2N}{N+2}$![]() . Then
. Then
and for any $p>1$![]() ,
,
where $C$![]() , $\tilde C$
, $\tilde C$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $k$
, it depends only on $k$![]() , $\chi$
, $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
In addition, by (3.28), and combining with Neumann heat semigroup theory, it is also easy to obtain the $L^\infty$![]() estimation of $\nabla \omega$
estimation of $\nabla \omega$![]() (depending on $\varepsilon$
(depending on $\varepsilon$![]() ). Furthermore, by (3.28) and Lemma 3.7, using standard Morser iterative technique, the $L^\infty$
). Furthermore, by (3.28) and Lemma 3.7, using standard Morser iterative technique, the $L^\infty$![]() estimation of $u$
estimation of $u$![]() is also easy to obtain.
is also easy to obtain.
Lemma 3.8 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Assume that $m>\frac {2N}{N+2}$
. Assume that $m>\frac {2N}{N+2}$![]() . Then
. Then
where $C_\varepsilon$![]() depends on $\varepsilon$
depends on $\varepsilon$![]() , and is independent of $T_{\max }$
, and is independent of $T_{\max }$![]() .
.
Using lemmas 3.1, 3.7, and 3.8, the solution of the regularized problem (3.1) exists globally for any $\varepsilon >0$![]() , and these estimations in lemma 3.2-Lemma 3.7 are independent of $\varepsilon$
, and these estimations in lemma 3.2-Lemma 3.7 are independent of $\varepsilon$![]() . To obtain the global solution to the original problem (1.6), we also need to make some a priori estimates for $u_t$
. To obtain the global solution to the original problem (1.6), we also need to make some a priori estimates for $u_t$![]() .
.
Lemma 3.9 Let $(u,\, v,\, \omega )$![]() be the classical solution of (3.1) in $[0,\, T_{\max })$
be the classical solution of (3.1) in $[0,\, T_{\max })$![]() . Assume that $m>\frac {2N}{N+2}$
. Assume that $m>\frac {2N}{N+2}$![]() . Then for any $1< r<2$
. Then for any $1< r<2$![]() , and any $T>0$
, and any $T>0$![]() ,
,
where $C_{T, r}$![]() depends on $T$
depends on $T$![]() , $r$
, $r$![]() , and it is independent of $\varepsilon$
, and it is independent of $\varepsilon$![]() .
.
Proof. For any $\varphi \in C^{\infty }(Q_T)$![]() , we see that
, we see that

Then for any $q>2$![]() , using (3.13), (3.28) and lemma 3.7, we derive that
, using (3.13), (3.28) and lemma 3.7, we derive that

namely for any $q>2$![]() ,
,
which implies (3.39).
Combining lemmas 3.1 -3.8, and noticing (3.16), we have the following proposition.
Proposition 3.10 Assume that $m>\frac {2N}{N+2}$![]() . For any $\varepsilon \in (0,\,1)$
. For any $\varepsilon \in (0,\,1)$![]() , the problem (3.1) in $[0,\, T_{\max })$
, the problem (3.1) in $[0,\, T_{\max })$![]() admits a unique positive global classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q)\cap C^0(\overline \Omega \times [0,\, \infty ))$
admits a unique positive global classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q)\cap C^0(\overline \Omega \times [0,\, \infty ))$![]() such that
such that
and for any $T>0$![]() ,
,

where $C_r$![]() , $C_T$
, $C_T$![]() , $C_{Tp}$
, $C_{Tp}$![]() , and $C_{Tr}$
, and $C_{Tr}$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() , they depend on $\chi$
, they depend on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() , $C_r$
, $C_r$![]() depends on $r$
depends on $r$![]() , $C_T$
, $C_T$![]() depends on $T$
depends on $T$![]() , $C_{Tp}$
, $C_{Tp}$![]() depends on $T$
depends on $T$![]() , $p$
, $p$![]() , and $C_{Tr}$
, and $C_{Tr}$![]() depends on $T$
depends on $T$![]() , $r$
, $r$![]() .
.
Proof of theorem 1.1 Since $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$![]() are classical solutions of (3.1), they obviously satisfy the equations (3.1) in the sense of distribution. By proposition 3.10, using Aubin-Lions lemma, and Sobolev compact embedding theorem, there exists a subsequence of $\{(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\}$
are classical solutions of (3.1), they obviously satisfy the equations (3.1) in the sense of distribution. By proposition 3.10, using Aubin-Lions lemma, and Sobolev compact embedding theorem, there exists a subsequence of $\{(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\}$![]() , which we still remember as itself for convenience, such that as $\varepsilon \to 0$
, which we still remember as itself for convenience, such that as $\varepsilon \to 0$![]() ,
,

Letting $\varepsilon \to 0$![]() and utilizing the above convergence results, we can ultimately verify that $(u,\, v,\, \omega )$
and utilizing the above convergence results, we can ultimately verify that $(u,\, v,\, \omega )$![]() satisfies definition 2.1, that is, $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$
satisfies definition 2.1, that is, $(u,\, v,\, \omega )\in \mathcal {X}_1\times \mathcal {X}_2\times \mathcal {X}_3$![]() is a weak solution. Theorem 1.1 is proved.
is a weak solution. Theorem 1.1 is proved.
4. Global solution to the haptotaxis-only system
In this section, we consider the haptotaxis-only system. Similar to § 2, to prove the existence of weak solutions, we consider the following regularized problem

Similar to § 3, in the subsequent energy estimate calculations, we omit the subscript $\varepsilon$![]() of the approximate solutions $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$
of the approximate solutions $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )$![]() in the subsequent energy estimate calculations.
in the subsequent energy estimate calculations.
It is clear that lemmas 3.1, 3.2, and 3.3 also hold for $\chi =0$![]() . Similar to lemma 3.4, we also have
. Similar to lemma 3.4, we also have
Lemma 4.1 Let $(u,\, v,\, \omega )$![]() be the classical solution of (4.1) in $[0,\, T_{\max })$
be the classical solution of (4.1) in $[0,\, T_{\max })$![]() . Then
. Then

where $C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $\chi$
, it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() . In addition, we also have
. In addition, we also have
and for any $1< p<2$![]() ,
,
where $C_T$![]() , $C_{Tp}$
, $C_{Tp}$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() , and $C_T$
, and $C_T$![]() depends on $T$
depends on $T$![]() , $C_{Tp}$
, $C_{Tp}$![]() depends on $T$
depends on $T$![]() and $p$
and $p$![]() .
.
Proof. Similar to the proof of (3.18), we see that

that is

Then completely similar to the proof of lemma 3.4, we complete the proof.
Completely similar to lemma 3.5, we also have that
Lemma 4.2 Let $(u,\, v,\, \omega )$![]() be the classical solution of (4.1) in $[0,\, T_{\max })$
be the classical solution of (4.1) in $[0,\, T_{\max })$![]() . Then for any $r>2$
. Then for any $r>2$![]() ,
,

where $\tilde C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $\chi$
, it depends only on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $r$
, $r$![]() , $\Omega$
, $\Omega$![]() .
.
Then similar to lemma 3.6, we also have that
Lemma 4.3 Let $(u,\, v,\, \omega )$![]() be the classical solution of (4.1) in $[0,\, T_{\max })$
be the classical solution of (4.1) in $[0,\, T_{\max })$![]() . Then for any positive integer $k$
. Then for any positive integer $k$![]() , we have that
, we have that

where $C$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $T_{\max }$
and $T_{\max }$![]() , it depends only on $k$
, it depends only on $k$![]() , $\chi$
, $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() .
.
Proof. For any given positive integer $k$![]() , multiplying both sides of the first equation of (4.1) by $(\frac {m}{m-1}(u+\varepsilon )^{m-1}-\xi \omega )^{2k+1}$
, multiplying both sides of the first equation of (4.1) by $(\frac {m}{m-1}(u+\varepsilon )^{m-1}-\xi \omega )^{2k+1}$![]() , and noticing that $\omega$
, and noticing that $\omega$![]() is bounded, then we arrive at
is bounded, then we arrive at

Combining with (3.30), and using (3.31) yields

By (4.6), (2.5), and using $L^p$![]() theory of linear parabolic equations, we arrive at
theory of linear parabolic equations, we arrive at

Then (4.7) is proved.
Completely similar to lemmas 3.7– 3.9. We have the following results.
Proposition 4.4 For any $\varepsilon \in (0,\,1)$![]() , the problem (4.1) admits a unique positive global classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q)\cap C^0(\overline \Omega \times [0,\, \infty ))$
, the problem (4.1) admits a unique positive global classical solution $(u_\varepsilon,\, v_\varepsilon,\, \omega _\varepsilon )\in C^{2, 1}(Q)\cap C^0(\overline \Omega \times [0,\, \infty ))$![]() such that
such that
and for any $T>0$![]() ,
,

where $C_r$![]() , $C_T$
, $C_T$![]() , $C_{Tp}$
, $C_{Tp}$![]() , and $C_{Tr}$
, and $C_{Tr}$![]() are independent of $\varepsilon$
are independent of $\varepsilon$![]() , they depend on $\chi$
, they depend on $\chi$![]() , $\xi$
, $\xi$![]() , $m$
, $m$![]() , $\mu$
, $\mu$![]() , $\eta$
, $\eta$![]() , $u_0$
, $u_0$![]() , $v_0$
, $v_0$![]() , $\omega _0$
, $\omega _0$![]() , $\Omega$
, $\Omega$![]() , $C_r$
, $C_r$![]() depends on $r$
depends on $r$![]() , $C_T$
, $C_T$![]() depends on $T$
depends on $T$![]() , $C_{Tp}$
, $C_{Tp}$![]() depends on $T$
depends on $T$![]() , $p$
, $p$![]() , and $C_{Tr}$
, and $C_{Tr}$![]() depends on $T$
depends on $T$![]() , $r$
, $r$![]() .
.
Letting $\varepsilon \to 0$![]() , we complete the proof of Theorem 1.2.
, we complete the proof of Theorem 1.2.
Acknowledgements
The author is supported by NSFC(12271186,12171166).
Statements and declarations
The author declares that there is no competing interest, and confirms that the data supporting the findings of this study are available within the paper.