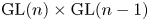 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
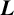 $\boldsymbol {L}$
-VALUES
$\boldsymbol {L}$
-VALUES