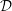 ${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
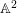 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 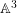 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
 ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
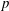 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration