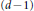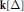15 results
Product decompositions of moment-angle manifolds and B-rigidity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1313-1325
- Print publication:
- December 2023
-
- Article
- Export citation
Equivariant cohomology of torus orbifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 299-328
- Print publication:
- April 2022
-
- Article
- Export citation
ON THE DEPTH OF SYMBOLIC POWERS OF EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 28-40
- Print publication:
- March 2022
-
- Article
- Export citation
Tight closure of powers of ideals and tight hilbert polynomials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 335-355
- Print publication:
- September 2020
-
- Article
- Export citation
Linear syzygies, hyperbolic Coxeter groups and regularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1076-1097
- Print publication:
- June 2019
-
- Article
- Export citation
Newton Complementary Duals of
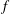 $f$-Ideals
$f$-Ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 231-241
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Wedge Operations and Torus Symmetries II
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 767-789
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
LYUBEZNIK NUMBERS OF LOCAL RINGS AND LINEAR STRANDS OF GRADED IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 23-54
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
GORENSTEIN AND Sr PATH IDEALS OF CYCLES
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 7-15
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
On the k-Buchsbaum property of powers of Stanley–Reisner ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 213 / March 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 127-140
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Alternative polarizations of Borel fixed ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 207 / September 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 79-93
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Face Ring Multiplicity via CM-Connectivity Sequences
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 4 / 01 August 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 888-903
- Print publication:
- 01 August 2009
-
- Article
-
- You have access
- Export citation
Gorenstein rings through face rings of manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 993-1000
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Dualizing Complex of a Toric Face Ring
-
- Journal:
- Nagoya Mathematical Journal / Volume 196 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 87-116
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Shellability of semigroup rings
-
- Journal:
- Nagoya Mathematical Journal / Volume 168 / 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 65-84
- Print publication:
- 2002
-
- Article
-
- You have access
- Export citation

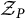







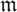 ) be an analytically unramified local ring of positive prime characteristic
) be an analytically unramified local ring of positive prime characteristic 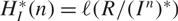
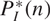
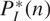
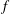
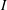
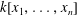
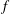
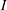
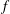
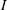
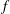
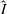
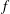
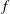
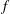
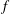
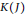
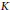
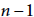
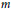
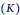
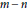
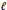
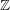
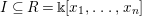
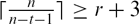
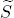 such that
such that 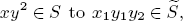 ours sends it to
ours sends it to