We discuss the
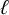 $\ell $
-adic case of Mazur’s ‘Program B’ over
$\ell $
-adic case of Mazur’s ‘Program B’ over
 $\mathbb {Q}$
: the problem of classifying the possible images of
$\mathbb {Q}$
: the problem of classifying the possible images of
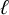 $\ell $
-adic Galois representations attached to elliptic curves E over
$\ell $
-adic Galois representations attached to elliptic curves E over
 $\mathbb {Q}$
, equivalently, classifying the rational points on the corresponding modular curves. The primes
$\mathbb {Q}$
, equivalently, classifying the rational points on the corresponding modular curves. The primes
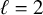 $\ell =2$
and
$\ell =2$
and
 $\ell \ge 13$
are addressed by prior work, so we focus on the remaining primes
$\ell \ge 13$
are addressed by prior work, so we focus on the remaining primes
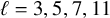 $\ell = 3, 5, 7, 11$
. For each of these
$\ell = 3, 5, 7, 11$
. For each of these
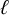 $\ell $
, we compute the directed graph of arithmetically maximal
$\ell $
, we compute the directed graph of arithmetically maximal
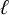 $\ell $
-power level modular curves
$\ell $
-power level modular curves
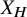 $X_H$
, compute explicit equations for all but three of them and classify the rational points on all of them except
$X_H$
, compute explicit equations for all but three of them and classify the rational points on all of them except
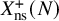 $X_{\mathrm {ns}}^{+}(N)$
, for
$X_{\mathrm {ns}}^{+}(N)$
, for
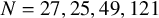 $N = 27, 25, 49, 121$
and two-level
$N = 27, 25, 49, 121$
and two-level
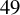 $49$
curves of genus
$49$
curves of genus
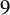 $9$
whose Jacobians have analytic rank
$9$
whose Jacobians have analytic rank
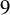 $9$
.
$9$
.
Aside from the
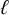 $\ell $
-adic images that are known to arise for infinitely many
$\ell $
-adic images that are known to arise for infinitely many
 ${\overline {\mathbb {Q}}}$
-isomorphism classes of elliptic curves
${\overline {\mathbb {Q}}}$
-isomorphism classes of elliptic curves
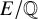 $E/\mathbb {Q}$
, we find only 22 exceptional images that arise for any prime
$E/\mathbb {Q}$
, we find only 22 exceptional images that arise for any prime
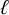 $\ell $
and any
$\ell $
and any
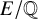 $E/\mathbb {Q}$
without complex multiplication; these exceptional images are realised by 20 non-CM rational j-invariants. We conjecture that this list of 22 exceptional images is complete and show that any counterexamples must arise from unexpected rational points on
$E/\mathbb {Q}$
without complex multiplication; these exceptional images are realised by 20 non-CM rational j-invariants. We conjecture that this list of 22 exceptional images is complete and show that any counterexamples must arise from unexpected rational points on
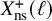 $X_{\mathrm {ns}}^+(\ell )$
with
$X_{\mathrm {ns}}^+(\ell )$
with
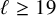 $\ell \ge 19$
, or one of the six modular curves noted above. This yields a very efficient algorithm to compute the
$\ell \ge 19$
, or one of the six modular curves noted above. This yields a very efficient algorithm to compute the
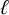 $\ell $
-adic images of Galois for any elliptic curve over
$\ell $
-adic images of Galois for any elliptic curve over
 $\mathbb {Q}$
.
$\mathbb {Q}$
.
In an appendix with John Voight, we generalise Ribet’s observation that simple abelian varieties attached to newforms on
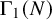 $\Gamma _1(N)$
are of
$\Gamma _1(N)$
are of
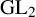 $\operatorname {GL}_2$
-type; this extends Kolyvagin’s theorem that analytic rank zero implies algebraic rank zero to isogeny factors of the Jacobian of
$\operatorname {GL}_2$
-type; this extends Kolyvagin’s theorem that analytic rank zero implies algebraic rank zero to isogeny factors of the Jacobian of
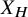 $X_H$
.
$X_H$
.
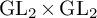 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
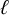 $\ell $
-adic images of Galois for elliptic curves over
$\ell $
-adic images of Galois for elliptic curves over
 $\mathbb {Q}$
(and an appendix with John Voight)
$\mathbb {Q}$
(and an appendix with John Voight)