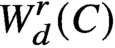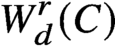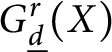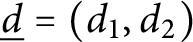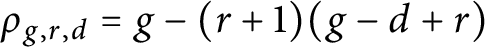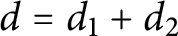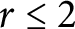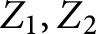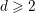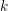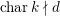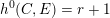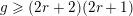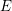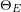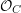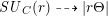12 results
Covering gonality of symmetric products of curves and Cayley–Bacharach condition on Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interpolation for Brill–Noether curves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vector bundles and finite covers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brill-Noether theory for curves of a fixed gonality
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 January 2021, e1
-
- Article
-
- You have access
- Open access
- Export citation
Brill-Noether generality of binary curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 787-807
- Print publication:
- December 2021
-
- Article
- Export citation
Gonality of dynatomic curves and strong uniform boundedness of preperiodic points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 733-743
- Print publication:
- April 2020
-
- Article
- Export citation
Tangent cones to generalised theta divisors and generic injectivity of the theta map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2643-2657
- Print publication:
- December 2017
-
- Article
- Export citation
HYPERELLIPTIC GRAPHS AND METRIZED COMPLEXES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 30 August 2017, e20
-
- Article
-
- You have access
- Open access
- Export citation
The extremal secant conjecture for curves of arbitrary gonality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 347-357
- Print publication:
- February 2017
-
- Article
- Export citation
Lifting Divisors on a Generic Chain of Loops
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 250-262
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
SEMIPOSITIVE BUNDLES AND BRILL–NOETHER THEORY
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 179-190
- Print publication:
- March 2003
-
- Article
- Export citation