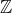 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
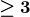 $\boldsymbol{\geq 3}$
$\boldsymbol{\geq 3}$
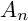 $A_n$ SINGULARITY
$A_n$ SINGULARITY
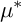 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES