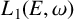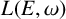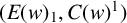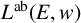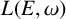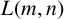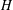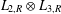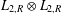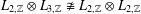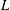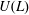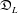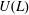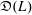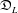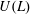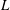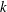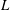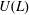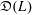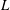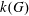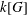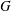8 results
The socle of subshift algebras, with applications to subshift conjugacy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
LEAVITT PATH ALGEBRAS OF WEIGHTED AND SEPARATED GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1-25
- Print publication:
- August 2023
-
- Article
- Export citation
TENSOR PRODUCTS OF STEINBERG ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 111-126
- Print publication:
- August 2021
-
- Article
- Export citation
Free Group Algebras in Division Rings with Valuation II
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 05 July 2019, pp. 1463-1504
- Print publication:
- December 2020
-
- Article
- Export citation
DIFFERENTIAL GRADED ENDOMORPHISM ALGEBRAS, COHOMOLOGY RINGS AND DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 557-573
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The Nilpotent Regular Element Problem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 461-471
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
FACTOR ALGEBRAS OF FREE ALGEBRAS: ON A PROBLEM OF G. BERGMAN
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 13 August 2003, pp. 706-710
- Print publication:
- September 2003
-
- Article
- Export citation
Resolutions of Associative and Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-16
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation