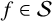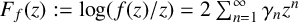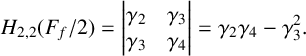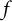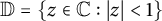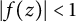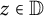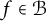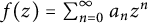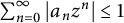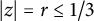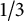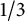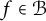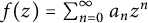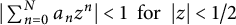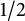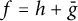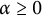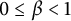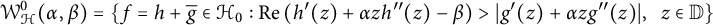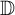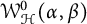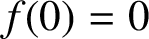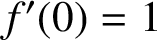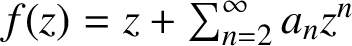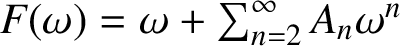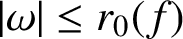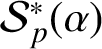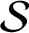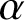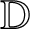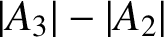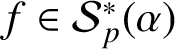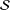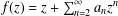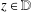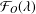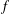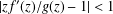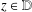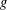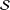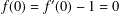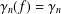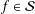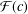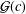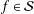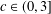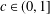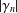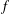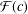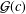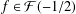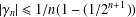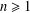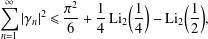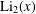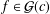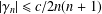12 results
Second Hankel determinant of logarithmic coefficients of inverse strongly starlike functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 1196-1211
-
- Article
-
- You have access
- HTML
- Export citation
THE SHARP BOUND OF THE SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS FOR STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
SECOND HANKEL DETERMINANT FOR LOGARITHMIC INVERSE COEFFICIENTS OF CONVEX AND STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 128-139
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
THE THIRD HANKEL DETERMINANT FOR INVERSE COEFFICIENTS OF CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 94-100
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
On a class of difference operator and its applications to a family of analytic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 248-258
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 1014-1029
- Print publication:
- September 2023
-
- Article
- Export citation
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
- Print publication:
- February 2022
-
- Article
- Export citation
ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 18 June 2020, pp. 124-131
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLOSE-TO-CONVEX ANALOGUE OF CERTAIN STARLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 22 January 2020, pp. 268-281
- Print publication:
- October 2020
-
- Article
- Export citation
LOGARITHMIC COEFFICIENTS PROBLEMS IN FAMILIES RELATED TO STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 230-249
- Print publication:
- October 2020
-
- Article
- Export citation
More Eventual Positivity for Analytic Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 5 / 01 October 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1019-1079
- Print publication:
- 01 October 2003
-
- Article
-
- You have access
- Export citation
On the logarithmic coefficients of close-to-convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation