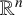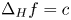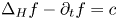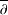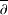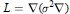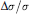11 results
ON MARCH’S CRITERION FOR TRANSIENCE ON ROTATIONALLY SYMMETRIC MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-11
-
- Article
- Export citation
AN OBSERVATION ON THE DIRICHLET PROBLEM AT INFINITY IN RIEMANNIAN CONES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 352-364
- Print publication:
- June 2023
-
- Article
- Export citation
A note on monotonicity and Bochner formulas in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1543-1563
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LANDAU’S THEOREM FOR SOLUTIONS OF THE
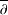 $\overline{\unicode[STIX]{x2202}}$-EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$-EQUATION IN DIRICHLET-TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 80-87
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES, LANDAU’S THEOREM AND LIPSCHITZ-TYPE SPACES ON PLANAR HARMONIC MAPPINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 198-215
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
MEAN VALUE TYPE INEQUALITIES FOR QUASINEARLY SUBHARMONIC FUNCTIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 349-368
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
Harmonic morphisms applied to classical potential theory
-
- Journal:
- Nagoya Mathematical Journal / Volume 202 / June 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 107-126
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
HARMONIC FUNCTION SPACES ON GROUPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 70 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 23 July 2004, pp. 182-198
- Print publication:
- August 2004
-
- Article
- Export citation
A LIOUVILLE THEOREM FOR MATRIX-VALUED HARMONIC FUNCTIONS ON NILPOTENT GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 14 August 2003, pp. 651-658
- Print publication:
- September 2003
-
- Article
- Export citation
On the Liouville Property for Divergence Form Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 3 / 01 June 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 487-496
- Print publication:
- 01 June 1998
-
- Article
-
- You have access
- Export citation
A Lower Estimate for Central Probabilities on Polycyclic Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 5 / 01 October 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-910
- Print publication:
- 01 October 1992
-
- Article
-
- You have access
- Export citation