We show that if 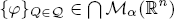 is a frame and {ψQ}Q∈Q ∈ ∩ Mα(ℝn) is its dual frame (for the definition of Mα(ℝn), see Definition 2.1), where Q is the collection of dyadic cubes, then for any f ∈ S′(ℝn), there exists a sequence of polynomials, PL,L′,L″, such that
is a frame and {ψQ}Q∈Q ∈ ∩ Mα(ℝn) is its dual frame (for the definition of Mα(ℝn), see Definition 2.1), where Q is the collection of dyadic cubes, then for any f ∈ S′(ℝn), there exists a sequence of polynomials, PL,L′,L″, such that
(0.1) 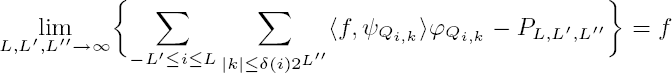
in the topology of S′(ℝn), where δ(i) = max(2i, 1). We prove this result by explicitly constructing the polynomials PL,L′,L″. Furthermore, using the above result, we assert that the linear span of the one-dimensional wavelet system is dense in a function space if and only if the dual space of this function space has an trivial intersection with the set of polynomials. This is proved by using the annihilator of the one-dimensional wavelet system.
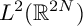 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
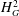 $H_{G}^{2}$
$H_{G}^{2}$