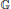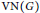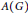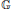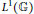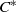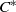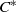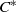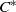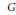8 results
Projective freeness and stable rank of algebras of complex-valued BV functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 844-853
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact structures for operator modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 421-446
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Amenability and Covariant Injectivity of Locally Compact Quantum Groups II
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 5 / 01 October 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1064-1086
- Print publication:
- 01 October 2017
-
- Article
-
- You have access
- Export citation
A Homological Property and Arens Regularity of Locally Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-130
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
THE SIMILARITY DEGREE OF SOME
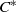 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 June 2013, pp. 60-69
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
EXTENSIONS OF BOHR'S INEQUALITY
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 6 / December 2006
- Published online by Cambridge University Press:
- 19 December 2006, pp. 991-999
- Print publication:
- December 2006
-
- Article
- Export citation
Biprojectivity and Biflatness for Convolution Algebras of Nuclear Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-455
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
Tensor Algebras, Induced Representations, and the Wold Decomposition
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 4 / 01 August 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 850-880
- Print publication:
- 01 August 1999
-
- Article
-
- You have access
- Export citation