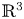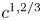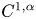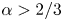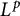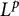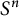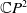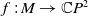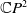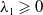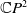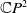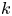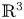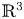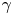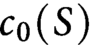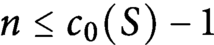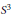13 results
The geometry of C1,α flat isometric immersions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anisotropic flow, entropy, and
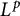 $L^p$-Minkowski problem
$L^p$-Minkowski problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-20
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Helfrich functional for compact surfaces in
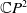 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 36-50
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
On k-folding map-germs and hidden symmetries of surfaces in the Euclidean 3-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 60-104
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonrigidity of flat ribbons
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 1297-1314
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Plongements polyédraux tendus et nombre chromatique relatif des surfaces à bord
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1001-1013
- Print publication:
- December 2021
-
- Article
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
Evolutes and focal surfaces of framed immersions in the Euclidean space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 497-516
- Print publication:
- February 2020
-
- Article
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
DIRECT EXPRESSION OF INCOMPATIBILITY IN CURVILINEAR SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 33-50
-
- Article
-
- You have access
- Export citation
Geometric Invariants of Cuspidal Edges
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-462
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
Helices, Hasimoto Surfaces and Bäcklund Transformations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 4 / 01 December 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 427-439
- Print publication:
- 01 December 2000
-
- Article
-
- You have access
- Export citation