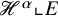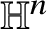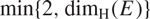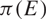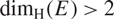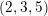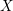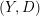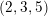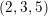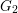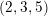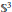13 results
On sets with unit Hausdorff density in homogeneous groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Carnot metrics, dynamics and local rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 614-664
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Riemannian approximation in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1139-1154
- Print publication:
- October 2022
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
DUALITY OF (2, 3, 5)-DISTRIBUTIONS AND LAGRANGIAN CONE STRUCTURES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 23 January 2020, pp. 303-315
- Print publication:
- September 2021
-
- Article
- Export citation
SUB-RIEMANNIAN RICCI CURVATURES AND UNIVERSAL DIAMETER BOUNDS FOR 3-SASAKIAN MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 21 June 2017, pp. 783-827
- Print publication:
- July 2019
-
- Article
- Export citation
SUB-RIEMANNIAN STRUCTURES ON GROUPS OF DIFFEOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 10 August 2015, pp. 745-785
- Print publication:
- September 2017
-
- Article
- Export citation
SubRiemannian Geometry on the Sphere 𝕊3
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 4 / 01 August 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-739
- Print publication:
- 01 August 2009
-
- Article
-
- You have access
- Export citation
CONTACT AND PANSU DIFFERENTIABLE MAPS ON CARNOT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 495-507
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Geodesics in a Manifold with Heisenberg Group as Boundary
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 3 / 01 June 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 566-589
- Print publication:
- 01 June 2004
-
- Article
-
- You have access
- Export citation
The Heat Kernel and Green's Function on a Manifold with Heisenberg Group as Boundary
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 3 / 01 June 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 590-611
- Print publication:
- 01 June 2004
-
- Article
-
- You have access
- Export citation