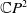 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
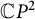 $\mathbb {C}P^{2}$ and
$\mathbb {C}P^{2}$ and 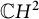 $\mathbb {C}H^{2}$
$\mathbb {C}H^{2}$
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
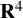 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
 $L^p$ harmonic 1-forms on hypersurfaces with finite index
$L^p$ harmonic 1-forms on hypersurfaces with finite index