22 results
Linear homeomorphisms of function spaces and the position of a space in its compactification
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2151-2172
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
LOGICS FROM ULTRAFILTERS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NULL SETS AND COMBINATORIAL COVERING PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1231-1242
- Print publication:
- September 2022
-
- Article
- Export citation
GAMES AND HEREDITARY BAIRENESS IN HYPERSPACES AND SPACES OF PROBABILITY MEASURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 851-868
- Print publication:
- May 2022
-
- Article
- Export citation
A Common Extension of Arhangel’skĭ’s Theorem and the Hajnal–Juhász Inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 06 January 2020, pp. 197-203
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Normality Versus Paracompactness in Locally Compact Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-96
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
PRODUCTS OF HUREWICZ SPACES IN THE LAVER MODEL
-
- Journal:
- Bulletin of Symbolic Logic / Volume 23 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 04 December 2017, pp. 324-333
- Print publication:
- September 2017
-
- Article
- Export citation
Topological Games and Alster Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 683-696
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
On the Hereditary Paracompactness of Locally Compact, Hereditarily Normal Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-584
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
ON
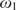 ${\omega _1}$-STRONGLY COMPACT CARDINALS
${\omega _1}$-STRONGLY COMPACT CARDINALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 266-278
- Print publication:
- March 2014
-
- Article
- Export citation
Productively Lindelöf Spaces May All Be D
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 203-212
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
PFA(S)[S]: More Mutually Consistent Topological Consequences of PFA and V = L
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 5 / 01 October 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1182-1200
- Print publication:
- 01 October 2012
-
- Article
-
- You have access
- Export citation
A NOTE ON PARACOMPACT p-SPACES AND THE MONOTONE D-PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 463-469
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
AN ANSWER TO VAN MILL’S QUESTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 353-355
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
The Normality in Products with a Countably Compact Factor
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 2 / 01 June 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 245-251
- Print publication:
- 01 June 1998
-
- Article
-
- You have access
- Export citation
On the Cardinality of Urysohn Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 2 / 01 June 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 153-158
- Print publication:
- 01 June 1988
-
- Article
-
- You have access
- Export citation
Rectangularity Versus Piecewise Rectangularity of Product Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 1 / 01 March 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-56
- Print publication:
- 01 March 1987
-
- Article
-
- You have access
- Export citation
The Almost Lindelöf Degree
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-455
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation
The Shrinking Property
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 4 / 01 December 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-388
- Print publication:
- 01 December 1983
-
- Article
-
- You have access
- Export citation
A Class of Spaces in Which Compact Sets are Finite
-
- Journal:
- Canadian Mathematical Bulletin / Volume 24 / Issue 3 / 01 September 1981
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-375
- Print publication:
- 01 September 1981
-
- Article
-
- You have access
- Export citation




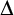
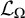
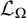
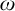
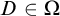
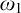
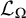

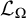
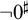
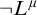
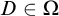
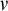
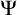
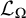
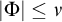

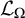
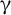
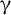
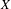
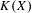
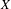
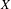
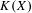
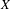
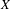

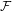
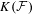
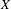
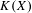
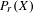
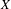
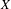
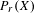
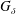
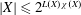
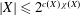
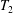
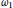
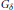
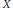
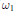
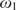
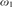
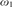
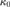
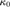
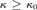
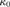
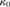




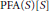
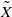 be the minimal dense linearly ordered extension of
be the minimal dense linearly ordered extension of 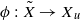 , ϕ(〈
, ϕ(〈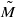 is a paracompact
is a paracompact 
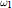
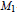
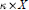
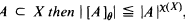 where [A]θ denotes the θ-closed hull of A, i.e., the smallest θ-closed subset of X containing A;
where [A]θ denotes the θ-closed hull of A, i.e., the smallest θ-closed subset of X containing A;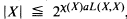 , where aL(X, X) is the smallest cardinal number m such that for every open cover
, where aL(X, X) is the smallest cardinal number m such that for every open cover 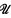 of X there is a subfamily
of X there is a subfamily 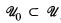 for which
for which 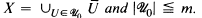

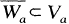 for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.
for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.