13 results
Discrete group actions on 3-manifolds and embeddable Cayley complexes
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
-
- You have access
- HTML
- Export citation
DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 329-345
- Print publication:
- March 2019
-
- Article
- Export citation
AVERAGING FORMULA FOR NIELSEN NUMBERS OF MAPS ON INFRA-SOLVMANIFOLDS OF TYPE (R) – CORRIGENDUM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 207-212
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
ON THE ALGEBRAIC CONVERGENCE OF FINITELY GENERATED KLEINIAN GROUPS IN ALL DIMENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 275-279
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
JØRGENSEN’S INEQUALITY FOR QUATERNIONIC HYPERBOLIC SPACE WITH ELLIPTIC ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 121-131
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Averaging Formula for Nielsen Numbers of Maps on Infra-Solvmanifolds of Type (R)
-
- Journal:
- Nagoya Mathematical Journal / Volume 196 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 117-134
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Averaging formula for Nielsen coincidence numbers
-
- Journal:
- Nagoya Mathematical Journal / Volume 186 / 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 69-93
- Print publication:
- 2007
-
- Article
-
- You have access
- Export citation
Averaging Formula for Nielsen Numbers
-
- Journal:
- Nagoya Mathematical Journal / Volume 178 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 37-53
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
On the Stable Basin Theorem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-444
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
Quaternions and Some Global Properties of Hyperbolic 5-Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 5 / 01 October 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1080-1099
- Print publication:
- 01 October 2003
-
- Article
-
- You have access
- Export citation
The Symmetries of Genus One Handlebodies
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 2 / 01 April 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-404
- Print publication:
- 01 April 1991
-
- Article
-
- You have access
- Export citation
A Group Theoretic Characterization of the 2-Dimensional Spherical Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 4 / 01 December 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-466
- Print publication:
- 01 December 1989
-
- Article
-
- You have access
- Export citation

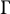
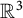
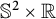
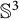
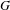
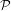
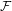
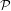
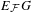
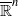 . In this paper, we prove that if {
. In this paper, we prove that if {
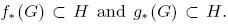 Then we investigate the conditions for which the following averaging formula holds
Then we investigate the conditions for which the following averaging formula holds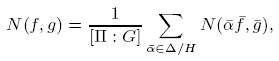
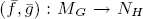 is any pair of fixed liftings of (
is any pair of fixed liftings of (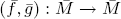 on the nil-covering
on the nil-covering 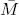 of
of 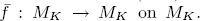 . We prove a question raised by McCord, which is for any
. We prove a question raised by McCord, which is for any 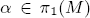 with
with 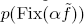 an essential fixed point class, fix
an essential fixed point class, fix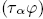 =1. As a consequence, we obtain the following averaging formula for Nielsen numbers
=1. As a consequence, we obtain the following averaging formula for Nielsen numbers