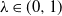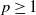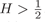48 results
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1196-1198
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 12 January 2024, pp. 503-538
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ESSAYS ON STRONG AND WEAK APPROXIMATIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 175-176
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Sandwiched SDEs with unbounded drift driven by Hölder noises
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 927-964
- Print publication:
- September 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact simulation of coupled Wright–Fisher diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 923-950
- Print publication:
- December 2021
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Self-exciting multifractional processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 22-41
- Print publication:
- March 2021
-
- Article
- Export citation
Stochastic differential equations driven by fractional Brownian motion with locally Lipschitz drift and their implicit Euler approximation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1278-1304
- Print publication:
- August 2021
-
- Article
- Export citation
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
- Print publication:
- September 2020
-
- Article
- Export citation
An analytic study of vibrational energy harvesting using piezoelectric tiles in stairways subjected to human traffic
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 08 October 2018, pp. 968-985
-
- Article
- Export citation
On the stochastic dynamics of a nonlinear vibration energy harvester driven by Lévy flight excitations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 08 October 2018, pp. 945-967
-
- Article
- Export citation
Approximate analytical solutions for a class of nonlinear stochastic differential equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 928-944
-
- Article
- Export citation
Targeted energy transfer in stochastically excited system with nonlinear energy sink
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 869-886
-
- Article
- Export citation
Applications of Magnus expansions and pseudospectra to Markov processes
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 April 2018, pp. 400-425
-
- Article
- Export citation
Itô-Taylor Schemes for Solving Mean-Field Stochastic Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 798-828
- Print publication:
- November 2017
-
- Article
- Export citation
Optimal Error Estimates for a Fully Discrete Euler Scheme for Decoupled Forward Backward Stochastic Differential Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 548-565
- Print publication:
- August 2017
-
- Article
- Export citation
Hybrid PDE solver for data-driven problems and modern branching†
-
- Journal:
- European Journal of Applied Mathematics / Volume 28 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 22 May 2017, pp. 949-972
-
- Article
-
- You have access
- Export citation
Deferred Correction Methods for Forward Backward Stochastic Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 222-242
- Print publication:
- May 2017
-
- Article
- Export citation