 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
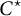 $C^\star $-algebras
$C^\star $-algebras
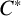 $\mathbf{\mathit{C}}^{*}$
-ALGEBRAS WHICH DETECT NUCLEARITY
$\mathbf{\mathit{C}}^{*}$
-ALGEBRAS WHICH DETECT NUCLEARITY
 $\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
$\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
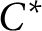 $C^*$
-algebra structure on certain Banach algebra products
$C^*$
-algebra structure on certain Banach algebra products
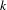 $k$-graph C*-algebras
$k$-graph C*-algebras