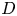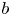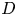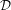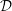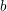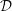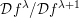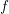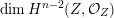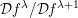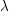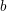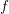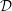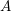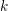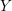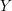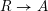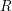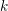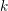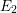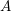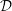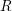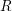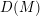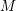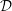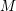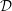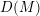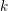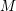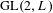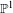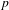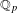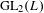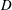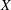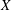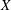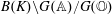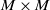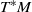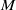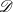9 results
A generalization of the b-function lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 September 2021, pp. 2199-2214
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IRREGULAR HODGE FILTRATION OF SOME CONFLUENT HYPERGEOMETRIC SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 May 2019, pp. 627-668
- Print publication:
- March 2021
-
- Article
- Export citation
On
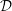 ${\mathcal{D}}$-modules related to the
${\mathcal{D}}$-modules related to the 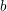 $b$-function and Hamiltonian flow
$b$-function and Hamiltonian flow
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 12 October 2018, pp. 2426-2440
- Print publication:
- November 2018
-
- Article
- Export citation
On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 2075-2146
- Print publication:
- October 2017
-
- Article
- Export citation
LOCALLY ANALYTIC REPRESENTATIONS OF
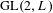 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 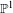 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 January 2017, pp. 125-187
- Print publication:
- January 2019
-
- Article
- Export citation
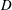 $D$-modules on spaces of rational maps
$D$-modules on spaces of rational maps
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 835-876
- Print publication:
- May 2014
-
- Article
- Export citation
Microlocal Euler classes and Hochschild homology
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 487-516
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
Croissance des Solutions des $\cal D$-Modules algébriques holonomes – (Growth of solutions of holonomic algebraic $\cal D$-modules)
-
- Journal:
- Compositio Mathematica / Volume 128 / Issue 2 / September 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 115-152
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
Vanishing Cycles of Irregular D-Modules
-
- Journal:
- Compositio Mathematica / Volume 116 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 241-310
- Print publication:
- May 1999
-
- Article
-
- You have access
- Export citation