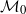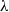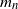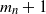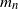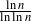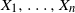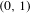Refine search
Actions for selected content:
60 results
Multivariate regular variation of preferential attachment models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1068-1100
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Probabilistic Modelling of Primary Loading and Hull Girder Response
-
- Book:
- Global Strength of Ships
- Published online:
- 20 March 2025
- Print publication:
- 03 April 2025, pp 404-471
-
- Chapter
- Export citation
Asymptotics for the conditional higher moment coherent risk measure with weak contagion
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 55 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 121-143
- Print publication:
- January 2025
-
- Article
- Export citation
9 - The Modeling of Extreme Events
-
- Book:
- Risk Revealed
- Published online:
- 05 April 2024
- Print publication:
- 11 April 2024, pp 219-291
-
- Chapter
- Export citation
An extreme worst-case risk measure by expectile
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1195-1214
- Print publication:
- December 2024
-
- Article
- Export citation
Information-theoretic convergence of extreme values to the Gumbel distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 June 2023, pp. 244-254
- Print publication:
- March 2024
-
- Article
- Export citation
Limit theory for U-statistics under geometric and topological constraints with rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 314-340
- Print publication:
- March 2023
-
- Article
- Export citation
Modeling and simulating spatial extremes by combining extreme value theory with generative adversarial networks
-
- Journal:
- Environmental Data Science / Volume 1 / 2022
- Published online by Cambridge University Press:
- 13 April 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Species Accumulation Curves and Extreme Value Theory
- from Part III - Theoretical Advances in Species–Area Relationship Research
-
-
- Book:
- The Species–Area Relationship
- Published online:
- 11 March 2021
- Print publication:
- 18 March 2021, pp 211-226
-
- Chapter
- Export citation
Oscillations for order statistics of some discrete processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 703-719
- Print publication:
- September 2020
-
- Article
- Export citation
AN ANALYTICAL APPROACH FOR THE BREAKDOWN DISTRIBUTION OF A THIN OXIDE
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 595-610
-
- Article
- Export citation
Gumbel and Fréchet convergence of the maxima of independent random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 213-236
- Print publication:
- March 2020
-
- Article
- Export citation
ON MARINE LIABILITY PORTFOLIO MODELING
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 13 December 2019, pp. 61-93
- Print publication:
- January 2020
-
- Article
- Export citation
Continued fractions, the Chen–Stein method and extreme value theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 461-470
- Print publication:
- February 2021
-
- Article
- Export citation
CAT BOND PRICING UNDER A PRODUCT PROBABILITY MEASURE WITH POT RISK CHARACTERIZATION
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 49 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 24 April 2019, pp. 457-490
- Print publication:
- May 2019
-
- Article
- Export citation
A large sample test for the length of memory of stationary symmetric stable random fields via nonsingular ℤd-actions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 179-195
- Print publication:
- March 2018
-
- Article
- Export citation
Equivalent representations of max-stable processes via ℓp-norms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 54-68
- Print publication:
- March 2018
-
- Article
- Export citation
ANALYZING AND PREDICTING CAT BOND PREMIUMS: A FINANCIAL LOSS PREMIUM PRINCIPLE AND EXTREME VALUE MODELING
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 48 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 375-411
- Print publication:
- January 2018
-
- Article
- Export citation
Marginal standardization of upper semicontinuous processes. With application to max-stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 773-796
- Print publication:
- September 2017
-
- Article
- Export citation
Extreme events of Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 134-161
- Print publication:
- March 2017
-
- Article
- Export citation