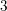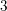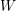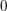We prove the genus-one restriction of the all-genus Landau–Ginzburg/Calabi–Yau conjecture of Chiodo and Ruan, stated in terms of the geometric quantization of an explicit symplectomorphism determined by genus-zero invariants. This gives the first evidence supporting the higher-genus Landau–Ginzburg/Calabi–Yau correspondence for the quintic $3$-fold, and exhibits the first instance of the ‘genus zero controls higher genus’ principle, in the sense of Givental’s quantization formalism, for non-semisimple cohomological field theories.

In this work we prove the so-called dimension property for the cohomological field theory associated with a homogeneous polynomial 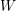$W$ with an isolated singularity, in the algebraic framework of [A. Polishchuk and A. Vaintrob, Matrix factorizations and cohomological field theories, J. Reine Angew. Math. 714 (2016), 1–122]. This amounts to showing that some cohomology classes on the Deligne–Mumford moduli spaces of stable curves, constructed using Fourier–Mukai-type functors associated with matrix factorizations, live in prescribed dimension. The proof is based on a homogeneity result established in [A. Polishchuk and A. Vaintrob, Algebraic construction of Witten’s top Chern class, in Advances in algebraic geometry motivated by physics (Lowell, MA, 2000) (American Mathematical Society, Providence, RI, 2001), 229–249] for certain characteristic classes of Koszul matrix factorizations of 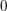$0$ . To reduce to this result, we use the theory of Fourier–Mukai-type functors involving matrix factorizations and the natural rational lattices in the relevant Hochschild homology spaces, as well as a version of Hodge–Riemann bilinear relations for Hochschild homology of matrix factorizations. Our approach also gives a proof of the dimension property for the cohomological field theories associated with some quasihomogeneous polynomials with an isolated singularity.