Refine search
Actions for selected content:
18 results
ON A CONJECTURE REGARDING THE MOUSE ORDER FOR WEASELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 364-390
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 1 - Introduction
-
- Book:
- The Largest Suslin Axiom
- Published online:
- 07 June 2024
- Print publication:
- 27 June 2024, pp 1-8
-
- Chapter
- Export citation

The Largest Suslin Axiom
-
- Published online:
- 07 June 2024
- Print publication:
- 27 June 2024
THE DEFINABILITY OF THE EXTENDER SEQUENCE
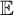 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 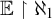 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 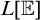 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTE ON
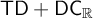 $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 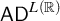 $\mathsf {AD}^{L(\mathbb {R})}$
$\mathsf {AD}^{L(\mathbb {R})}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 211-217
- Print publication:
- March 2024
-
- Article
- Export citation
DIVERGENT MODELS WITH THE FAILURE OF THE CONTINUUM HYPOTHESIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 December 2023, pp. 1-11
-
- Article
- Export citation
NEGATIVE RESULTS ON PRECIPITOUS IDEALS ON
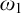 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 490-509
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
$\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 871-896
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEALING OF THE UNIVERSALLY BAIRE SETS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 254-266
- Print publication:
- September 2021
-
- Article
- Export citation
THE CONSISTENCY STRENGTH OF LONG PROJECTIVE DETERMINACY
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 November 2019, pp. 338-366
- Print publication:
- March 2020
-
- Article
- Export citation
LARGE CARDINALS BEYOND CHOICE
-
- Journal:
- Bulletin of Symbolic Logic / Volume 25 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 20 August 2019, pp. 283-318
- Print publication:
- September 2019
-
- Article
- Export citation
AN ANALYSIS OF THE MODELS
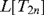 $L[T_{2n} ]$
$L[T_{2n} ]$
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 February 2019, pp. 1-26
- Print publication:
- March 2019
-
- Article
- Export citation
VARSOVIAN MODELS I
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 496-528
- Print publication:
- June 2018
-
- Article
- Export citation
THE MOUSE SET CONJECTURE FOR SETS OF REALS
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 April 2015, pp. 671-683
- Print publication:
- June 2015
-
- Article
- Export citation
Non-tame Mice from Tame Failures of the Unique Branch Hypothesis
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 903-923
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
Descriptive inner model theory
-
- Journal:
- Bulletin of Symbolic Logic / Volume 19 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 05 September 2014, pp. 1-55
- Print publication:
- March 2013
-
- Article
- Export citation
The largest countable inductive set is a mouse set
-
- Journal:
- The Journal of Symbolic Logic / Volume 64 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 12 March 2014, pp. 443-459
- Print publication:
- June 1999
-
- Article
- Export citation
Some applications of coarse inner model theory
-
- Journal:
- The Journal of Symbolic Logic / Volume 62 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 12 March 2014, pp. 337-365
- Print publication:
- June 1997
-
- Article
- Export citation









 -Woodin cardinal. On the other hand, we show thatassuming there is no transitive model of KP with a Woodin cardinal theconjecture holds. In the course of this we will also show that if
-Woodin cardinal. On the other hand, we show thatassuming there is no transitive model of KP with a Woodin cardinal theconjecture holds. In the course of this we will also show that if




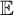
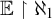
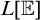
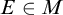
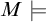
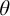
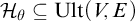
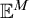
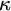
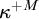
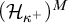
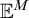
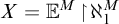
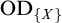
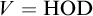
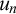
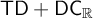
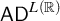
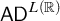
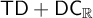





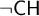
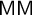
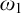
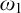


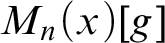
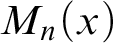
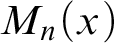
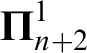
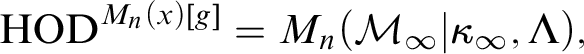
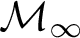
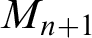
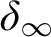
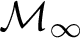
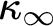
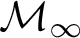
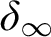
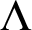

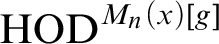








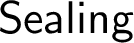











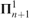
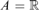
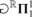
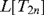
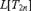
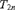
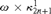
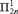
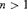
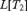
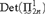
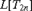
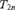
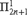
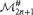
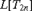

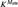
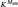
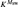
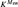

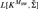
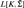


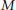
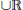
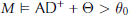
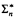 real is in
real is in 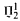 determinacy implies that for every thin
determinacy implies that for every thin 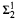 equivalence relation there is a
equivalence relation there is a 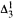 real,
real, 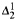 (
(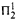 prewellorder has rank less than
prewellorder has rank less than 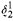 .
.