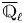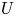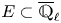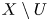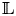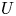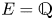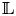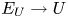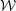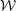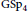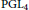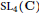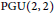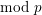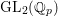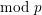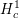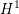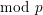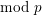Constructing abelian varieties from rank 2 Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 709-731
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Le transfert singulier pour la formule des traces de Jacquet–Rallis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 16 March 2021, pp. 303-434
- Print publication:
- February 2021
-
- Article
- Export citation
Quantum Langlands duality of representations of {\mathcal{W}}-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2235-2262
- Print publication:
- December 2019
-
- Article
- Export citation
Multivariate Rankin–Selberg Integrals on GL4 and GU(2, 2)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 822-835
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
Constructing elliptic curves from Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 29 August 2018, pp. 2045-2054
- Print publication:
- October 2018
-
- Article
- Export citation
On \text{mod}~p non-abelian Lubin–Tate theory for \text{GL}_{2}(\mathbb{Q}_{p})
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 12 March 2015, pp. 1433-1461
- Print publication:
- August 2015
-
- Article
- Export citation