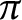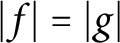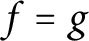13 results
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Learning-based surface deformation recovery for large radio telescope antennas
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 6 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 935-945
-
- Article
-
- You have access
- HTML
- Export citation
Zernike-coefficient extraction via helical beam reconstruction for optimization (ZEHBRO) in the far field
-
- Journal:
- High Power Laser Science and Engineering / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 July 2023, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fourier Ptychography Part II: Phase Retrieval and High-Resolution Image Formation
-
- Journal:
- / Volume 30 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 September 2022, pp. 36-39
- Print publication:
- September 2022
-
- Article
-
- You have access
- HTML
- Export citation
Live Processing of Momentum-Resolved STEM Data for First Moment Imaging and Ptychography
-
- Journal:
- / Volume 27 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 05 August 2021, pp. 1078-1092
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering Matrix Determination in Crystalline Materials from 4D Scanning Transmission Electron Microscopy at a Single Defocus Value
-
- Journal:
- / Volume 27 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 27 July 2021, pp. 744-757
- Print publication:
- August 2021
-
- Article
- Export citation
A note on the phase retrieval of holomorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 779-786
- Print publication:
- December 2021
-
- Article
- Export citation
Investigation on the Dependency of Phase Retrieval Accuracy Versus Edge Enhancement to the Noise Ratio of X-ray Propagation-Based Phase-Contrast Imaging
-
- Journal:
- / Volume 25 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 13 August 2019, pp. 1201-1212
- Print publication:
- October 2019
-
- Article
- Export citation
An online diagnosis technique for simultaneous measurement of the fundamental, second and third harmonics in one snapshot
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Application of convex optimization to identification of atomic species from diffraction patterns
-
- Journal:
- Powder Diffraction / Volume 32 / Issue S1 / September 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. S179-S185
-
- Article
- Export citation
Fast Deterministic Ptychographic Imaging Using X-Rays
-
- Journal:
- / Volume 20 / Issue 4 / August 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 1090-1099
- Print publication:
- August 2014
-
- Article
- Export citation
Focal-Series Reconstruction in Low-Energy Electron Microscopy
-
- Journal:
- / Volume 20 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 09 April 2014, pp. 968-973
- Print publication:
- June 2014
-
- Article
- Export citation
Determining convex polygons from their covariograms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 261-266
- Print publication:
- June 2002
-
- Article
- Export citation