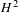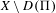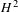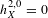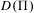Refine search
Actions for selected content:
6 results
1 - Differentiable manifolds
- from Part I - Mathematical background
-
- Book:
- Quantum Geometry, Matrix Theory, and Gravity
- Published online:
- 04 April 2024
- Print publication:
- 11 April 2024, pp 3-12
-
- Chapter
- Export citation
ERRATUM/CORRIGENDUM, OCTOBER 2020, FOR ’A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION’ (J. INST. MATH. JUSSIEU 19 (2018), 1509–1519)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 April 2021, pp. 275-277
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
SNC Log Symplectic Structures on Fano Products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 891-900
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 09 November 2018, pp. 1509-1519
- Print publication:
- September 2020
-
- Article
- Export citation
Elliptic singularities on log symplectic manifolds and Feigin–Odesskii Poisson brackets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 717-744
- Print publication:
- April 2017
-
- Article
- Export citation
On the local structure of Dirac manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 774-786
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation