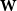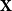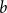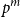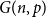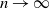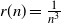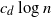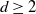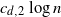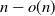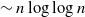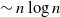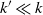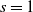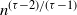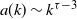Refine search
Actions for selected content:
85 results
The distance on the slightly supercritical random series–parallel graph
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-22
-
- Article
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Behaviour of the minimum degree throughout the
 ${\textit{d}}$-process
${\textit{d}}$-process
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 564-582
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random multi-hooking networks
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 13 February 2023, pp. 100-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Girth, magnitude homology and phase transition of diagonality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 221-247
- Print publication:
- February 2024
-
- Article
- Export citation
Random networks grown by fusing edges via urns
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 03 November 2022, pp. 347-360
-
- Article
- Export citation
On connectivity and robustness of random graphs with inhomogeneity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 284-294
- Print publication:
- March 2023
-
- Article
- Export citation
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
Prevalence of deficiency-zero reaction networks in an Erdös–Rényi framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 384-398
- Print publication:
- June 2022
-
- Article
- Export citation
On model selection for dense stochastic block models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 January 2022, pp. 202-226
- Print publication:
- March 2022
-
- Article
- Export citation
Depths in hooking networks
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 941-949
-
- Article
- Export citation
THE NEAREST UNVISITED VERTEX WALK ON RANDOM GRAPHS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 851-867
-
- Article
-
- You have access
- Open access
- Export citation
Scale-free percolation in continuous space: quenched degree and clustering coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 106-127
- Print publication:
- March 2021
-
- Article
- Export citation
Randomized near-neighbor graphs, giant components and applications in data science
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 458-476
- Print publication:
- June 2020
-
- Article
- Export citation
Moments of k-hop counts in the random-connection model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1106-1121
- Print publication:
- December 2019
-
- Article
- Export citation
Transient and slim versus recurrent and fat: Random walks and the trees they grow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 769-786
- Print publication:
- September 2019
-
- Article
- Export citation
Degree correlations in scale-free random graph models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 672-700
- Print publication:
- September 2019
-
- Article
- Export citation
6 - A counterexample to questions about boundaries, stability, and commensurability
- from Part Three - Research Articles
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 151-159
-
- Chapter
- Export citation