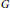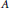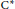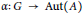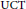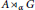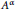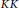3 results
A Short Note on the Continuous Rokhlin Property and the Universal Coefficient Theorem in E-theory
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 374-380
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Non-splitting in Kirchberg's Ideal-related KK-Theory
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 68-81
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
The Baum-Connes conjecture for KK-theory
-
- Journal:
- Journal of K-Theory / Volume 8 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 07 April 2010, pp. 3-29
- Print publication:
- August 2011
-
- Article
- Export citation