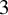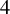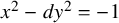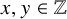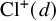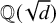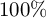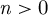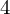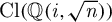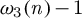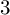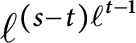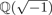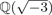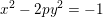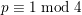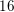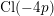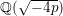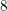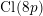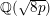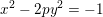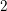13 results
On class groups of upper cluster algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-21
-
- Article
- Export citation
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
The 8-rank of the narrow class group and the negative Pell equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 June 2022, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE
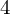 $4$
-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
$4$
-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1543-1570
- Print publication:
- September 2022
-
- Article
- Export citation
On the compositum of orthogonal cyclic fields of the same odd prime degree
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 14 July 2020, pp. 1506-1530
- Print publication:
- December 2021
-
- Article
- Export citation
Growth of Fine Selmer Groups in Infinite Towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 921-936
- Print publication:
- December 2020
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Spins of prime ideals and the negative Pell equation
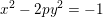 $x^{2}-2py^{2}=-1$
$x^{2}-2py^{2}=-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 100-125
- Print publication:
- January 2019
-
- Article
- Export citation
A non-abelian Stickelberger theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 01 July 2010, pp. 35-55
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Corrigendum: on the mean 3-rank of quadratic fields
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 04 December 2007, p. 1221
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
Gras-Type Conjectures Fattitle for Function Fields
-
- Journal:
- Compositio Mathematica / Volume 118 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 263-290
- Print publication:
- September 1999
-
- Article
-
- You have access
- Export citation
On the Mean 3-Rank of Quadratic Fields
-
- Journal:
- Compositio Mathematica / Volume 118 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-9
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
On a Refined Stark Conjecture for Function Fields
-
- Journal:
- Compositio Mathematica / Volume 116 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 04 December 2007, pp. 321-367
- Print publication:
- May 1999
-
- Article
-
- You have access
- Export citation