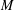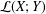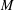4 results
Geometric Characterizations of Hilbert Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 769-775
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
BIRKHOFF ORTHOGONALITY IN CLASSICAL
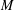 $M$-IDEALS
$M$-IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 279-288
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A CONTINUITY CHARACTERIZATION OF ASPLUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 450-455
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
On the LLN for the number of vertices of a random convex hull
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 675-681
- Print publication:
- September 2000
-
- Article
- Export citation