Refine search
Actions for selected content:
11 results
A NEW LINEAR AND CONSERVATIVE FINITE DIFFERENCE SCHEME FOR THE GROSS–PITAEVSKII EQUATION WITH ANGULAR MOMENTUM ROTATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 08 April 2019, pp. 204-232
-
- Article
-
- You have access
- Export citation
An Unconditionally Stable and High-Order Convergent Difference Scheme for Stokes’ First Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 597-613
- Print publication:
- August 2017
-
- Article
- Export citation
Numerical Solution to the Multi-Term Time Fractional Diffusion Equation in a Finite Domain
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-357
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Effect of Geometric Conservation Law on Improving Spatial Accuracy for Finite Difference Schemes on Two-Dimensional Nonsmooth Grids
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 14 September 2015, pp. 673-706
- Print publication:
- September 2015
-
- Article
- Export citation
Uniformly Stable Explicitly Solvable Finite Difference Method for Fractional Diffusion Equations
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 5 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 29-47
- Print publication:
- February 2015
-
- Article
- Export citation
A Remark on the Courant-Friedrichs-Lewy Condition in Finite Difference Approach to PDE’s
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 5 / October 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 693-698
- Print publication:
- October 2014
-
- Article
- Export citation
A High-Accuracy Finite Difference Scheme for Solving Reaction-Convection-Diffusion Problems with a Small Diffusivity
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 5 / October 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 637-662
- Print publication:
- October 2014
-
- Article
- Export citation
Numerical Method for Singularly Perturbed Third Order Ordinary Differential Equations of Convection-Diffusion Type
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 265-287
- Print publication:
- August 2014
-
- Article
- Export citation
A note on (2K+1)-point conservative monotone schemes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 345-357
- Print publication:
- March 2004
-
- Article
- Export citation
Convergence of a numerical scheme for a nonlinear oblique derivative boundary value problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1111-1132
- Print publication:
- November 2002
-
- Article
- Export citation
Convergence of finite difference schemes for viscousand inviscid conservation laws with rough coefficients
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 35 / Issue 2 / March 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 239-269
- Print publication:
- March 2001
-
- Article
- Export citation
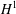
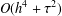

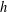
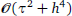 in maximum norm, where
in maximum norm, where 