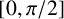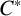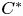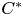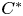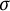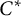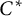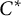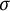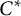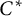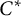3 results
ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 44-66
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Strong morita equivalence for conditional expectations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 182-213
-
- Article
- Export citation
The Picard groups of inclusions of
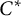 $C^*$
-algebras induced by equivalence bimodules
$C^*$
-algebras induced by equivalence bimodules
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 743-758
- Print publication:
- September 2022
-
- Article
- Export citation