The object of this paper is to prove a version of the Beurling–Helson–Lowdenslager invariant subspace theorem for operators on certain Banach spaces of functions on a multiply connected domain in $\mathbb{C}$. The norms for these spaces are either the usual Lebesgue and Hardy space norms or certain continuous gauge norms. In the Hardy space case the expected corollaries include the characterization of the cyclic vectors as the outer functions in this context, a demonstration that the set of analytic multiplication operators is maximal abelian and reflexive, and a determination of the closed operators that commute with all analytic multiplication operators.

The theory of almost invariant half-spaces for operators on Banach spaces was begun recently and is now under active development. Much less attention has been given to almost invariant half-spaces for operators on Hilbert space, where some techniques and results are available that are not present in the more general context of Banach spaces. In this note, we begin such a study. Our much simpler and shorter proofs of the main theorems have important consequences for the matricial structure of arbitrary operators on Hilbert space.

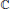
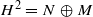Let M be a forward-shift-invariant subspace and N a backward-shift-invariant subspace in the Hardy space H2 on the bidisc. We assume that . Using the wandering subspace of M and N, we study the relations between M and N. Moreover we study M and N using several natural operators defined by shift operators on H2.

Let $L^{2}=L^{2}(D,rdrd\theta/\pi)$ be the Lebesgue space on the open unit disc $D$ and let $L_{a}^2=L^{2}\cap\mathrm{Hol}(D)$ be a Bergman space on $D$. In this paper, we are interested in a closed subspace $\mathcal{M}$ of $L^{2}$ which is invariant under the multiplication by the coordinate function $z$, and a Hankel-type operator from $L_{a}^2$ to $\mathcal{M}^\bot$. In particular, we study an invariant subspace $\mathcal{M}$ such that there does not exist a finite-rank Hankel-type operator except a zero operator.

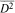Let be the closed bidisc and 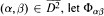T2 be its distinguished boundary. For be a slice map, that is, 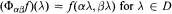and 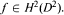Then ker Φ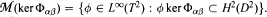αβ is an invariant subspace, and it is not difficult to describe ker Φαβ and In this paper, we study the set 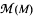of all multipliers for an invariant subspace M such that the common zero set of M contains that of ker Φαβ.