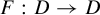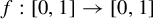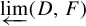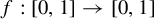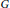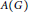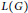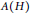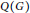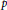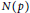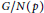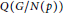10 results
On conjugacy of natural extensions of one-dimensional maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 2915-2937
- Print publication:
- September 2023
-
- Article
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation
1 - Basic Facts on Categories
-
- Book:
- Derived Categories
- Published online:
- 15 November 2019
- Print publication:
- 19 December 2019, pp 26-36
-
- Chapter
- Export citation
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
2 - Inverse Limits
-
- Book:
- Slenderness
- Published online:
- 30 November 2018
- Print publication:
- 06 December 2018, pp 91-118
-
- Chapter
- Export citation
Cokernels of Homomorphisms from Burnside Rings to Inverse Limits
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 165-172
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
A Remark on the Hull of a Multi-Dimensional Limit-PeriodicPotential
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 75-81
- Print publication:
- 2013
-
- Article
- Export citation
Adic Topologies for the Rational Integers
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 4 / 01 August 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 711-723
- Print publication:
- 01 August 2003
-
- Article
-
- You have access
- Export citation
Universal and proximately universal limits
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 96-105
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Continuum-Wise Expansive Homeomorphisms
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 3 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 576-598
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation